Galois ring
The Galois ring $ { \mathop{\rm GR} } ( p ^ {m} ,d ) $
is [a5] the unique Galois extension of $ \mathbf Z/ {p ^ {m} } \mathbf Z $
of degree $ d $.
For instance $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) $
is $ \mathbf Z/p ^ {m} \mathbf Z $
and $ { \mathop{\rm GR} } ( p,d ) $
is $ \mathbf F _ {p ^ {d} } $.
Generalizing finite fields (cf. Finite field), these rings find applications in similar areas: linear recurrences [a1], [a6], [a7], cyclic codes [a9], [a2] [a3], association schemes [a10], and character sums [a10], [a4]. For a connection with Witt rings see [a8] (cf. also Witt ring). Two different constructions of these rings are given below: bottom-up, starting from a finite field, and top-down, starting from a local field.
Bottom up.
This is the first and the most algorithmic one. Let $ n = p ^ {d} - 1 $. Pick an irreducible monic primitive polynomial $ {\overline{f}\; } $ of degree $ d $, as in the standard construction of $ \mathbf F _ {p ^ {d} } $ from $ \mathbf F _ {p} $, and lift it to a polynomial $ f $ over $ \mathbf Z/p ^ {m} \mathbf Z $ in such a way that the nice finite field property ( $ f $ divides $ X ^ {n} - 1 $) still holds. In the language of linear recurrences (or linear feedback shift registers), one has lifted an $ m $- sequence of period $ n $ over $ \mathbf F _ {p} $ into a linear recurrence over $ \mathbf Z/p ^ {m} \mathbf Z $ of the same period. This is construction $ A $ of [a1]. Note that an arbitrary lift will lead to multiplying the period by a power of $ p $, as in construction $ B $ of [a1]. For example, $ p = 2 $, $ f ( x ) = x ^ {2} + x + 1 $ gives a period $ 6 $ and not $ 3 $. Now, let
$$ { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z/p ^ {m} \mathbf Z [ X ] / ( f ) . $$
Top down.
This $ p $- adic approach was introduced in print in [a4] but was implicitly known to M. Yamada [a10], who used the term "Teichmüller" , as in $ p $- adic analysis, and also to E. Spiegel [a9]. Denote by $ \mathbf Z _ {p} $ the ring of $ p $- adic integers, best viewed as the set of formal expansions in powers of $ p $ with coefficients in the residue field $ \mathbf F _ {p} $. Then $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) = \mathbf Z _ {p} / ( p ^ {m} ) $. For higher values of $ d $ one considers the unramified extension of $ \mathbf Q _ {p} $ generated by $ \zeta _ {n} $( an $ n $- th root of unity) and its ring of integers $ \mathbf Z _ {p} [ \zeta _ {n} ] $. Let $ T _ {d} $ denote the set of $ p ^ {d} $ roots of $ 1 $ over this latter ring. This set of so-called Teichmüller representatives reduces modulo $ p $ to $ \mathbf F _ {p ^ {d} } $. The ring of integers of the $ p $- adic field admits the following expansion: $ \mathbf Z _ {p} [ \zeta _ {n} ] = \sum _ {i = 0 } ^ \infty p ^ {i} T ^ {i} $, which converges in the sense of the $ p $- adic valuation. Modulo $ p ^ {m} $ this yields
$$ { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z _ {p} [ \zeta _ {n} ] / ( p ^ {m} ) . $$
Multiplicative structure.
The ring $ R = { \mathop{\rm GR} } ( p ^ {m} ,d ) $ comprises units $ R ^ \times $ and zero divisors $ pR $. The multiplicative group $ R ^ \times $ is the direct product of $ T _ {d} \setminus \{ 0 \} $ by the group of so-called principal units $ 1 + pR $. The group of principal units is isomorphic, for $ m = 2 $ or $ p > 2 $, to the additive group of $ ( \mathbf Z/p ^ {m - 1 } \mathbf Z ) ^ {d} $. The Galois group of $ R $ over $ \mathbf Z/p ^ {m} \mathbf Z $ is isomorphic to the Galois group of $ \mathbf F _ {p ^ {d} } $ over $ \mathbf F _ {p} $ and therefore cyclic of order $ d $.
References
| [a1] | S. Boztas, A.R. Hammons, P.V. Kumar, "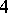 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" IEEE Inform. Th. , 41 (1995) pp. 366–376 |
| [a3] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 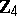 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a4] | V. Kumar, T. Helleseth, R.A. Calderbank, "An upper bound for Weil-type exponential sums over Galois rings and applications" IEEE Inform. Th. , 41 (1995) |
| [a5] | B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974) |
| [a6] | P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" G. Cohen (ed.) J. Wolfmann (ed.) , Coding Theory and Applications , Lecture Notes in Computer Science , 388 , Springer (1989) pp. 193–201 |
| [a7] | P. Udaya, M.U. Siddiqui, "Optimal biphase sequences with large linear complexity derived from sequences over 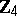 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 |
| [a8] | A.G. Shanbag, P.V. Kumar, T. Helleseth, "An upperbound for the extended Kloosterman sums over Galois rings" , Finite Fields and Applications (to appear) |
| [a9] | E. Spiegel, "Codes over 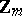 revisited" Inform. and Control , 37 (1978) pp. 100–104 revisited" Inform. and Control , 37 (1978) pp. 100–104 |
| [a10] | M. Yamada, "Distance regular graphs of girth 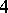 over an extension ring of over an extension ring of 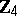 " Graphs and Combinatorics , 6 (1980) pp. 381–384 " Graphs and Combinatorics , 6 (1980) pp. 381–384 |
Galois ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_ring&oldid=47033