Difference between revisions of "Galois ring"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | g1100401.png | ||
| + | $#A+1 = 64 n = 6 | ||
| + | $#C+1 = 64 : ~/encyclopedia/old_files/data/G110/G.1100040 Galois ring | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | The Galois ring $ { \mathop{\rm GR} } ( p ^ {m} ,d ) $ | ||
| + | is [[#References|[a5]]] the unique [[Galois extension|Galois extension]] of $ \mathbf Z/ {p ^ {m} } \mathbf Z $ | ||
| + | of degree $ d $. | ||
| + | For instance $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) $ | ||
| + | is $ \mathbf Z/p ^ {m} \mathbf Z $ | ||
| + | and $ { \mathop{\rm GR} } ( p,d ) $ | ||
| + | is $ \mathbf F _ {p ^ {d} } $. | ||
| + | Generalizing finite fields (cf. [[Finite field|Finite field]]), these rings find applications in similar areas: linear recurrences [[#References|[a1]]], [[#References|[a6]]], [[#References|[a7]]], cyclic codes [[#References|[a9]]], [[#References|[a2]]] [[#References|[a3]]], association schemes [[#References|[a10]]], and character sums [[#References|[a10]]], [[#References|[a4]]]. For a connection with Witt rings see [[#References|[a8]]] (cf. also [[Witt ring|Witt ring]]). Two different constructions of these rings are given below: bottom-up, starting from a finite field, and top-down, starting from a [[Local field|local field]]. | ||
==Bottom up.== | ==Bottom up.== | ||
| − | This is the first and the most algorithmic one. Let | + | This is the first and the most algorithmic one. Let $ n = p ^ {d} - 1 $. |
| + | Pick an irreducible monic primitive [[Polynomial|polynomial]] $ {\overline{f}\; } $ | ||
| + | of degree $ d $, | ||
| + | as in the standard construction of $ \mathbf F _ {p ^ {d} } $ | ||
| + | from $ \mathbf F _ {p} $, | ||
| + | and lift it to a polynomial $ f $ | ||
| + | over $ \mathbf Z/p ^ {m} \mathbf Z $ | ||
| + | in such a way that the nice finite field property ( $ f $ | ||
| + | divides $ X ^ {n} - 1 $) | ||
| + | still holds. In the language of linear recurrences (or linear feedback shift registers), one has lifted an $ m $- | ||
| + | sequence of period $ n $ | ||
| + | over $ \mathbf F _ {p} $ | ||
| + | into a linear recurrence over $ \mathbf Z/p ^ {m} \mathbf Z $ | ||
| + | of the same period. This is construction $ A $ | ||
| + | of [[#References|[a1]]]. Note that an arbitrary lift will lead to multiplying the period by a power of $ p $, | ||
| + | as in construction $ B $ | ||
| + | of [[#References|[a1]]]. For example, $ p = 2 $, | ||
| + | $ f ( x ) = x ^ {2} + x + 1 $ | ||
| + | gives a period $ 6 $ | ||
| + | and not $ 3 $. | ||
| + | Now, let | ||
| − | + | $$ | |
| + | { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z/p ^ {m} \mathbf Z [ X ] / ( f ) . | ||
| + | $$ | ||
==Top down.== | ==Top down.== | ||
| − | This | + | This $ p $- |
| + | adic approach was introduced in print in [[#References|[a4]]] but was implicitly known to M. Yamada [[#References|[a10]]], who used the term "Teichmüller" , as in $ p $- | ||
| + | adic analysis, and also to E. Spiegel [[#References|[a9]]]. Denote by $ \mathbf Z _ {p} $ | ||
| + | the ring of $ p $- | ||
| + | adic integers, best viewed as the set of formal expansions in powers of $ p $ | ||
| + | with coefficients in the residue field $ \mathbf F _ {p} $. | ||
| + | Then $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) = \mathbf Z _ {p} / ( p ^ {m} ) $. | ||
| + | For higher values of $ d $ | ||
| + | one considers the unramified extension of $ \mathbf Q _ {p} $ | ||
| + | generated by $ \zeta _ {n} $( | ||
| + | an $ n $- | ||
| + | th root of unity) and its ring of integers $ \mathbf Z _ {p} [ \zeta _ {n} ] $. | ||
| + | Let $ T _ {d} $ | ||
| + | denote the set of $ p ^ {d} $ | ||
| + | roots of $ 1 $ | ||
| + | over this latter ring. This set of so-called Teichmüller representatives reduces modulo $ p $ | ||
| + | to $ \mathbf F _ {p ^ {d} } $. | ||
| + | The ring of integers of the $ p $- | ||
| + | adic field admits the following expansion: $ \mathbf Z _ {p} [ \zeta _ {n} ] = \sum _ {i = 0 } ^ \infty p ^ {i} T ^ {i} $, | ||
| + | which converges in the sense of the $ p $- | ||
| + | adic valuation. Modulo $ p ^ {m} $ | ||
| + | this yields | ||
| − | + | $$ | |
| + | { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z _ {p} [ \zeta _ {n} ] / ( p ^ {m} ) . | ||
| + | $$ | ||
==Multiplicative structure.== | ==Multiplicative structure.== | ||
| − | The ring | + | The ring $ R = { \mathop{\rm GR} } ( p ^ {m} ,d ) $ |
| + | comprises units $ R ^ \times $ | ||
| + | and zero divisors $ pR $. | ||
| + | The multiplicative group $ R ^ \times $ | ||
| + | is the direct product of $ T _ {d} \setminus \{ 0 \} $ | ||
| + | by the group of so-called principal units $ 1 + pR $. | ||
| + | The group of principal units is isomorphic, for $ m = 2 $ | ||
| + | or $ p > 2 $, | ||
| + | to the additive group of $ ( \mathbf Z/p ^ {m - 1 } \mathbf Z ) ^ {d} $. | ||
| + | The Galois group of $ R $ | ||
| + | over $ \mathbf Z/p ^ {m} \mathbf Z $ | ||
| + | is isomorphic to the Galois group of $ \mathbf F _ {p ^ {d} } $ | ||
| + | over $ \mathbf F _ {p} $ | ||
| + | and therefore cyclic of order $ d $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Boztas, A.R. Hammons, P.V. Kumar, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004067.png" />-phase sequence with near optimum correlation properties" ''IEEE Inform. Th.'' , '''38''' (1992) pp. 1101–1113</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" ''IEEE Inform. Th.'' , '''41''' (1995) pp. 366–376</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004068.png" />-linearity of Kerdock, Preparata, Goethals, and related codes" ''IEEE Trans. Information Th.'' , '''40''' (1994) pp. 301–319</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V. Kumar, T. Helleseth, R.A. Calderbank, "An upper bound for Weil-type exponential sums over Galois rings and applications" ''IEEE Inform. Th.'' , '''41''' (1995)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" G. Cohen (ed.) J. Wolfmann (ed.) , ''Coding Theory and Applications'' , ''Lecture Notes in Computer Science'' , '''388''' , Springer (1989) pp. 193–201</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P. Udaya, M.U. Siddiqui, "Optimal biphase sequences with large linear complexity derived from sequences over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004069.png" />" ''IEEE Inform. Th.'' , '''IT–42''' (1996) pp. 202–216</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A.G. Shanbag, P.V. Kumar, T. Helleseth, "An upperbound for the extended Kloosterman sums over Galois rings" , ''Finite Fields and Applications'' (to appear)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E. Spiegel, "Codes over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004070.png" /> revisited" ''Inform. and Control'' , '''37''' (1978) pp. 100–104</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Yamada, "Distance regular graphs of girth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004071.png" /> over an extension ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004072.png" />" ''Graphs and Combinatorics'' , '''6''' (1980) pp. 381–384</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Boztas, A.R. Hammons, P.V. Kumar, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004067.png" />-phase sequence with near optimum correlation properties" ''IEEE Inform. Th.'' , '''38''' (1992) pp. 1101–1113</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" ''IEEE Inform. Th.'' , '''41''' (1995) pp. 366–376</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004068.png" />-linearity of Kerdock, Preparata, Goethals, and related codes" ''IEEE Trans. Information Th.'' , '''40''' (1994) pp. 301–319</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V. Kumar, T. Helleseth, R.A. Calderbank, "An upper bound for Weil-type exponential sums over Galois rings and applications" ''IEEE Inform. Th.'' , '''41''' (1995)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" G. Cohen (ed.) J. Wolfmann (ed.) , ''Coding Theory and Applications'' , ''Lecture Notes in Computer Science'' , '''388''' , Springer (1989) pp. 193–201</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P. Udaya, M.U. Siddiqui, "Optimal biphase sequences with large linear complexity derived from sequences over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004069.png" />" ''IEEE Inform. Th.'' , '''IT–42''' (1996) pp. 202–216</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A.G. Shanbag, P.V. Kumar, T. Helleseth, "An upperbound for the extended Kloosterman sums over Galois rings" , ''Finite Fields and Applications'' (to appear)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E. Spiegel, "Codes over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004070.png" /> revisited" ''Inform. and Control'' , '''37''' (1978) pp. 100–104</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> M. Yamada, "Distance regular graphs of girth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004071.png" /> over an extension ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110040/g11004072.png" />" ''Graphs and Combinatorics'' , '''6''' (1980) pp. 381–384</TD></TR></table> | ||
Latest revision as of 19:40, 5 June 2020
The Galois ring $ { \mathop{\rm GR} } ( p ^ {m} ,d ) $
is [a5] the unique Galois extension of $ \mathbf Z/ {p ^ {m} } \mathbf Z $
of degree $ d $.
For instance $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) $
is $ \mathbf Z/p ^ {m} \mathbf Z $
and $ { \mathop{\rm GR} } ( p,d ) $
is $ \mathbf F _ {p ^ {d} } $.
Generalizing finite fields (cf. Finite field), these rings find applications in similar areas: linear recurrences [a1], [a6], [a7], cyclic codes [a9], [a2] [a3], association schemes [a10], and character sums [a10], [a4]. For a connection with Witt rings see [a8] (cf. also Witt ring). Two different constructions of these rings are given below: bottom-up, starting from a finite field, and top-down, starting from a local field.
Bottom up.
This is the first and the most algorithmic one. Let $ n = p ^ {d} - 1 $. Pick an irreducible monic primitive polynomial $ {\overline{f}\; } $ of degree $ d $, as in the standard construction of $ \mathbf F _ {p ^ {d} } $ from $ \mathbf F _ {p} $, and lift it to a polynomial $ f $ over $ \mathbf Z/p ^ {m} \mathbf Z $ in such a way that the nice finite field property ( $ f $ divides $ X ^ {n} - 1 $) still holds. In the language of linear recurrences (or linear feedback shift registers), one has lifted an $ m $- sequence of period $ n $ over $ \mathbf F _ {p} $ into a linear recurrence over $ \mathbf Z/p ^ {m} \mathbf Z $ of the same period. This is construction $ A $ of [a1]. Note that an arbitrary lift will lead to multiplying the period by a power of $ p $, as in construction $ B $ of [a1]. For example, $ p = 2 $, $ f ( x ) = x ^ {2} + x + 1 $ gives a period $ 6 $ and not $ 3 $. Now, let
$$ { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z/p ^ {m} \mathbf Z [ X ] / ( f ) . $$
Top down.
This $ p $- adic approach was introduced in print in [a4] but was implicitly known to M. Yamada [a10], who used the term "Teichmüller" , as in $ p $- adic analysis, and also to E. Spiegel [a9]. Denote by $ \mathbf Z _ {p} $ the ring of $ p $- adic integers, best viewed as the set of formal expansions in powers of $ p $ with coefficients in the residue field $ \mathbf F _ {p} $. Then $ { \mathop{\rm GR} } ( p ^ {m} ,1 ) = \mathbf Z _ {p} / ( p ^ {m} ) $. For higher values of $ d $ one considers the unramified extension of $ \mathbf Q _ {p} $ generated by $ \zeta _ {n} $( an $ n $- th root of unity) and its ring of integers $ \mathbf Z _ {p} [ \zeta _ {n} ] $. Let $ T _ {d} $ denote the set of $ p ^ {d} $ roots of $ 1 $ over this latter ring. This set of so-called Teichmüller representatives reduces modulo $ p $ to $ \mathbf F _ {p ^ {d} } $. The ring of integers of the $ p $- adic field admits the following expansion: $ \mathbf Z _ {p} [ \zeta _ {n} ] = \sum _ {i = 0 } ^ \infty p ^ {i} T ^ {i} $, which converges in the sense of the $ p $- adic valuation. Modulo $ p ^ {m} $ this yields
$$ { \mathop{\rm GR} } ( p ^ {m} ,d ) = \mathbf Z _ {p} [ \zeta _ {n} ] / ( p ^ {m} ) . $$
Multiplicative structure.
The ring $ R = { \mathop{\rm GR} } ( p ^ {m} ,d ) $ comprises units $ R ^ \times $ and zero divisors $ pR $. The multiplicative group $ R ^ \times $ is the direct product of $ T _ {d} \setminus \{ 0 \} $ by the group of so-called principal units $ 1 + pR $. The group of principal units is isomorphic, for $ m = 2 $ or $ p > 2 $, to the additive group of $ ( \mathbf Z/p ^ {m - 1 } \mathbf Z ) ^ {d} $. The Galois group of $ R $ over $ \mathbf Z/p ^ {m} \mathbf Z $ is isomorphic to the Galois group of $ \mathbf F _ {p ^ {d} } $ over $ \mathbf F _ {p} $ and therefore cyclic of order $ d $.
References
| [a1] | S. Boztas, A.R. Hammons, P.V. Kumar, "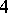 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | A. Bonnecaze, P. Solé, A.R. Calderbank, "Quaternary construction of unimodular lattices" IEEE Inform. Th. , 41 (1995) pp. 366–376 |
| [a3] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 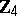 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a4] | V. Kumar, T. Helleseth, R.A. Calderbank, "An upper bound for Weil-type exponential sums over Galois rings and applications" IEEE Inform. Th. , 41 (1995) |
| [a5] | B.R. MacDonald, "Finite rings with identity" , M. Dekker (1974) |
| [a6] | P. Solé, "A quaternary cyclic code and a family of quaternary sequences with low correlation" G. Cohen (ed.) J. Wolfmann (ed.) , Coding Theory and Applications , Lecture Notes in Computer Science , 388 , Springer (1989) pp. 193–201 |
| [a7] | P. Udaya, M.U. Siddiqui, "Optimal biphase sequences with large linear complexity derived from sequences over 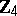 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 " IEEE Inform. Th. , IT–42 (1996) pp. 202–216 |
| [a8] | A.G. Shanbag, P.V. Kumar, T. Helleseth, "An upperbound for the extended Kloosterman sums over Galois rings" , Finite Fields and Applications (to appear) |
| [a9] | E. Spiegel, "Codes over 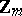 revisited" Inform. and Control , 37 (1978) pp. 100–104 revisited" Inform. and Control , 37 (1978) pp. 100–104 |
| [a10] | M. Yamada, "Distance regular graphs of girth 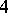 over an extension ring of over an extension ring of 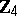 " Graphs and Combinatorics , 6 (1980) pp. 381–384 " Graphs and Combinatorics , 6 (1980) pp. 381–384 |
Galois ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_ring&oldid=47033