Difference between revisions of "Friedrichs inequality"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0417401.png | ||
| + | $#A+1 = 42 n = 2 | ||
| + | $#C+1 = 42 : ~/encyclopedia/old_files/data/F041/F.0401740 Friedrichs inequality | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
An inequality of the form | An inequality of the form | ||
| − | + | $$ \tag{1 } | |
| + | \int\limits _ \Omega f ^ { 2 } \ | ||
| + | d \Omega \leq C \left \{ | ||
| + | \int\limits _ \Omega | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | \left ( | ||
| + | |||
| + | \frac{\partial f }{\partial x _ {i} } | ||
| − | + | \right ) ^ {2} \ | |
| + | d \Omega + \int\limits _ \Gamma | ||
| + | f ^ { 2 } d \Gamma \right \} , | ||
| + | $$ | ||
| − | + | where $ \Omega $ | |
| + | is a bounded domain of points $ x = x ( x _ {1} \dots x _ {n} ) $ | ||
| + | in an $ n $- | ||
| + | dimensional Euclidean space with an $ ( n - 1) $- | ||
| + | dimensional boundary $ \Gamma $ | ||
| + | satisfying a local Lipschitz condition, and the function $ f \equiv f ( x) \in W _ {2} ^ {1} ( \Omega ) $( | ||
| + | a [[Sobolev space|Sobolev space]]). | ||
| − | + | The right-hand side of the Friedrichs inequality gives an equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $. | |
| + | Using another equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $, | ||
| + | one obtains (see [[#References|[2]]]) a modification of the Friedrichs inequality of the form | ||
| − | + | $$ \tag{2 } | |
| + | \int\limits _ \Omega f ^ { 2 } \ | ||
| + | d \Omega \leq C \left \{ | ||
| + | \int\limits _ \Omega | ||
| + | \sum _ {i = 1 } ^ { n } | ||
| + | \left ( | ||
| − | + | \frac{\partial f }{\partial x _ {i} } | |
| + | |||
| + | \right ) ^ {2} d \Omega + \left ( | ||
| + | \int\limits _ \Gamma f d \Gamma \right ) | ||
| + | ^ {2} \right \} . | ||
| + | $$ | ||
| + | |||
| + | There are generalizations (see [[#References|[3]]]–[[#References|[5]]]) of the Friedrichs inequality to weighted spaces (see [[Weighted space|Weighted space]]; [[Imbedding theorems|Imbedding theorems]]). Suppose that $ \Gamma \subset C ^ {(} l) $ | ||
| + | and that the numbers $ r $, | ||
| + | $ p $ | ||
| + | and $ \alpha $ | ||
| + | are real, with $ r $ | ||
| + | being a natural number and $ 1 \leq p < \infty $. | ||
| + | One says that $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ | ||
| + | if the norm | ||
| + | |||
| + | $$ | ||
| + | \| f \| _ {W _ {p, \alpha } ^ {r} ( \Omega ) } = \ | ||
| + | \| f \| _ {L _ {p} ( \Omega ) } + | ||
| + | \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } | ||
| + | $$ | ||
is finite, where | is finite, where | ||
| − | + | $$ | |
| + | \| f \| _ {L _ {p} ( \Omega ) } = \ | ||
| + | \left ( \int\limits _ \Omega | f | ^ {p} \ | ||
| + | d \Omega \right ) ^ {1/p} , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } | ||
| + | = \sum _ {| k | = r } \| \rho ^ \alpha f ^ {(} k) \| _ {L _ {p} ( \Omega ) } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | f ^ { ( k) } = | ||
| + | \frac{\partial ^ {| k | } f }{\partial x _ {1} ^ {k _ {1} } \dots \partial x _ {n} ^ {k _ {n} } } | ||
| + | ,\ \ | ||
| + | | k | = \sum _ {i = 1 } ^ { n } k _ {i} , | ||
| + | $$ | ||
| − | + | and $ \rho = \rho ( x) $ | |
| + | is distance function from $ x \in \Omega $ | ||
| + | to $ \Gamma $. | ||
| − | + | Suppose that $ s _ {0} $ | |
| + | is a natural number such that | ||
| − | + | $$ | |
| + | r - \alpha - { | ||
| + | \frac{1}{p} | ||
| + | } \leq \ | ||
| + | s _ {0} < r - \alpha + 1 - { | ||
| + | \frac{1}{p} | ||
| + | } . | ||
| + | $$ | ||
| − | < | + | Then, if $ \Gamma \subset C ^ {( s _ {0} + 1) } $, |
| + | $ - p ^ {-} 1 < \alpha < r - p ^ {-} 1 $, | ||
| + | $ r/2 \leq s _ {0} $, | ||
| + | for $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ | ||
| + | the following inequality holds: | ||
| − | + | $$ | |
| + | \| f \| _ {L _ {p} ( \Omega ) } \leq \ | ||
| + | C \left \{ | ||
| + | \sum _ {l + s < r/2 } | ||
| + | \left \| \left ( \left . | ||
| − | + | \frac{\partial ^ {s} f }{\partial n ^ {s} } | |
| + | \ | ||
| + | \right | _ \Gamma \right ) ^ {(} l) \ | ||
| + | \right \| _ {L _ {p} ( \Gamma ) } + | ||
| + | \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } | ||
| + | \right \} , | ||
| + | $$ | ||
| − | where | + | where $ ( \partial ^ {s} f/ \partial n ^ {s} ) \mid _ \Gamma $ |
| + | is the derivative of order $ s $ | ||
| + | with respect to the interior normal to $ \Gamma $ | ||
| + | at the points of $ \Gamma $. | ||
One can also obtain an inequality of the type (2), which has in the simplest case the form | One can also obtain an inequality of the type (2), which has in the simplest case the form | ||
| − | + | $$ | |
| + | \| f \| _ {L _ {p} ( \Omega ) } ^ {p} \leq \ | ||
| + | C \left ( | ||
| + | \| f \| _ {\omega _ {p, \alpha } ^ {1} ( \Omega ) } ^ {p} + | ||
| + | \left | \int\limits _ \Gamma | ||
| + | u \tau d \Gamma \ | ||
| + | \right | ^ {p} \right ) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | p , \gamma > 1,\ \ | ||
| + | - | ||
| + | \frac{1}{p} | ||
| + | < \alpha < 1 - | ||
| + | \frac{1}{p} | ||
| + | - | ||
| + | \frac{1} \gamma | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \tau \in L _ \gamma ( \Gamma ),\ \int\limits _ \Gamma \tau d \Gamma \neq 0. | ||
| + | $$ | ||
| − | The constant | + | The constant $ C $ |
| + | is independent of $ f $ | ||
| + | throughout. | ||
| − | The inequality is named after K.O. Friedrichs, who obtained it for | + | The inequality is named after K.O. Friedrichs, who obtained it for $ n = 2 $, |
| + | $ f \in C ^ {(} 2) ( \overline \Omega \; ) $( | ||
| + | see [[#References|[1]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> K.O. Friedrichs, "Eine invariante Formulierung des Newtonschen Gravititationsgesetzes und des Grenzüberganges vom Einsteinschen zum Newtonschen Gesetz" ''Math. Ann.'' , '''98''' (1927) pp. 566–575</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.M. Nikol'skii, P.I. Lizorkin, "On some inequalities for weight-class functions and boundary-value problems with a strong degeneracy at the boundary" ''Soviet Math. Dokl.'' , '''5''' (1964) pp. 1535–1539 ''Dokl. Akad. Nauk SSSR'' , '''159''' : 3 (1964) pp. 512–515</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D.F. Kalinichenko, "Some properties of functions in the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041740/f04174043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041740/f04174044.png" />" ''Mat. Sb.'' , '''64''' : 3 (1964) pp. 436–457 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Nirenberg, "On elliptic partial differential equations" ''Ann. Scuola Norm. Sup. Pisa Ser. 3'' , '''13''' : 2 (1959) pp. 115–162</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L. Sandgren, "A vibration problem" ''Medd. Lunds Univ. Mat. Sem.'' , '''13''' (1955) pp. 1–84</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K.O. Friedrichs, "Eine invariante Formulierung des Newtonschen Gravititationsgesetzes und des Grenzüberganges vom Einsteinschen zum Newtonschen Gesetz" ''Math. Ann.'' , '''98''' (1927) pp. 566–575</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.M. Nikol'skii, P.I. Lizorkin, "On some inequalities for weight-class functions and boundary-value problems with a strong degeneracy at the boundary" ''Soviet Math. Dokl.'' , '''5''' (1964) pp. 1535–1539 ''Dokl. Akad. Nauk SSSR'' , '''159''' : 3 (1964) pp. 512–515</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> D.F. Kalinichenko, "Some properties of functions in the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041740/f04174043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f041/f041740/f04174044.png" />" ''Mat. Sb.'' , '''64''' : 3 (1964) pp. 436–457 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Nirenberg, "On elliptic partial differential equations" ''Ann. Scuola Norm. Sup. Pisa Ser. 3'' , '''13''' : 2 (1959) pp. 115–162</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L. Sandgren, "A vibration problem" ''Medd. Lunds Univ. Mat. Sem.'' , '''13''' (1955) pp. 1–84</TD></TR></table> | ||
Latest revision as of 19:40, 5 June 2020
An inequality of the form
$$ \tag{1 } \int\limits _ \Omega f ^ { 2 } \ d \Omega \leq C \left \{ \int\limits _ \Omega \sum _ {i = 1 } ^ { n } \left ( \frac{\partial f }{\partial x _ {i} } \right ) ^ {2} \ d \Omega + \int\limits _ \Gamma f ^ { 2 } d \Gamma \right \} , $$
where $ \Omega $ is a bounded domain of points $ x = x ( x _ {1} \dots x _ {n} ) $ in an $ n $- dimensional Euclidean space with an $ ( n - 1) $- dimensional boundary $ \Gamma $ satisfying a local Lipschitz condition, and the function $ f \equiv f ( x) \in W _ {2} ^ {1} ( \Omega ) $( a Sobolev space).
The right-hand side of the Friedrichs inequality gives an equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $. Using another equivalent norm in $ W _ {2} ^ {1} ( \Omega ) $, one obtains (see [2]) a modification of the Friedrichs inequality of the form
$$ \tag{2 } \int\limits _ \Omega f ^ { 2 } \ d \Omega \leq C \left \{ \int\limits _ \Omega \sum _ {i = 1 } ^ { n } \left ( \frac{\partial f }{\partial x _ {i} } \right ) ^ {2} d \Omega + \left ( \int\limits _ \Gamma f d \Gamma \right ) ^ {2} \right \} . $$
There are generalizations (see [3]–[5]) of the Friedrichs inequality to weighted spaces (see Weighted space; Imbedding theorems). Suppose that $ \Gamma \subset C ^ {(} l) $ and that the numbers $ r $, $ p $ and $ \alpha $ are real, with $ r $ being a natural number and $ 1 \leq p < \infty $. One says that $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ if the norm
$$ \| f \| _ {W _ {p, \alpha } ^ {r} ( \Omega ) } = \ \| f \| _ {L _ {p} ( \Omega ) } + \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } $$
is finite, where
$$ \| f \| _ {L _ {p} ( \Omega ) } = \ \left ( \int\limits _ \Omega | f | ^ {p} \ d \Omega \right ) ^ {1/p} , $$
$$ \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } = \sum _ {| k | = r } \| \rho ^ \alpha f ^ {(} k) \| _ {L _ {p} ( \Omega ) } , $$
$$ f ^ { ( k) } = \frac{\partial ^ {| k | } f }{\partial x _ {1} ^ {k _ {1} } \dots \partial x _ {n} ^ {k _ {n} } } ,\ \ | k | = \sum _ {i = 1 } ^ { n } k _ {i} , $$
and $ \rho = \rho ( x) $ is distance function from $ x \in \Omega $ to $ \Gamma $.
Suppose that $ s _ {0} $ is a natural number such that
$$ r - \alpha - { \frac{1}{p} } \leq \ s _ {0} < r - \alpha + 1 - { \frac{1}{p} } . $$
Then, if $ \Gamma \subset C ^ {( s _ {0} + 1) } $, $ - p ^ {-} 1 < \alpha < r - p ^ {-} 1 $, $ r/2 \leq s _ {0} $, for $ f \in W _ {p, \alpha } ^ {r} ( \Omega ) $ the following inequality holds:
$$ \| f \| _ {L _ {p} ( \Omega ) } \leq \ C \left \{ \sum _ {l + s < r/2 } \left \| \left ( \left . \frac{\partial ^ {s} f }{\partial n ^ {s} } \ \right | _ \Gamma \right ) ^ {(} l) \ \right \| _ {L _ {p} ( \Gamma ) } + \| f \| _ {\omega _ {p, \alpha } ^ {r} ( \Omega ) } \right \} , $$
where $ ( \partial ^ {s} f/ \partial n ^ {s} ) \mid _ \Gamma $ is the derivative of order $ s $ with respect to the interior normal to $ \Gamma $ at the points of $ \Gamma $.
One can also obtain an inequality of the type (2), which has in the simplest case the form
$$ \| f \| _ {L _ {p} ( \Omega ) } ^ {p} \leq \ C \left ( \| f \| _ {\omega _ {p, \alpha } ^ {1} ( \Omega ) } ^ {p} + \left | \int\limits _ \Gamma u \tau d \Gamma \ \right | ^ {p} \right ) , $$
where
$$ p , \gamma > 1,\ \ - \frac{1}{p} < \alpha < 1 - \frac{1}{p} - \frac{1} \gamma , $$
$$ \tau \in L _ \gamma ( \Gamma ),\ \int\limits _ \Gamma \tau d \Gamma \neq 0. $$
The constant $ C $ is independent of $ f $ throughout.
The inequality is named after K.O. Friedrichs, who obtained it for $ n = 2 $, $ f \in C ^ {(} 2) ( \overline \Omega \; ) $( see [1]).
References
| [1] | K.O. Friedrichs, "Eine invariante Formulierung des Newtonschen Gravititationsgesetzes und des Grenzüberganges vom Einsteinschen zum Newtonschen Gesetz" Math. Ann. , 98 (1927) pp. 566–575 |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [3] | S.M. Nikol'skii, P.I. Lizorkin, "On some inequalities for weight-class functions and boundary-value problems with a strong degeneracy at the boundary" Soviet Math. Dokl. , 5 (1964) pp. 1535–1539 Dokl. Akad. Nauk SSSR , 159 : 3 (1964) pp. 512–515 |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [5] | D.F. Kalinichenko, "Some properties of functions in the spaces 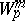 and and 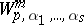 " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) |
| [6] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [7] | L. Nirenberg, "On elliptic partial differential equations" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 13 : 2 (1959) pp. 115–162 |
| [8] | L. Sandgren, "A vibration problem" Medd. Lunds Univ. Mat. Sem. , 13 (1955) pp. 1–84 |
Friedrichs inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Friedrichs_inequality&oldid=15223