Elliptic genera
The name elliptic genus has been given to various multiplicative cobordism invariants taking values in a ring of modular forms. The following is an attempt to present the simplest case — level- genera in characteristic
genera in characteristic  — in a unified way. It is convenient to use N. Katz's approach to modular forms (cf. [a7]) and view a modular form as a function of elliptic curves with a chosen invariant differential (cf. also Elliptic curve). A similar approach to elliptic genera was used by J. Franke [a3].
— in a unified way. It is convenient to use N. Katz's approach to modular forms (cf. [a7]) and view a modular form as a function of elliptic curves with a chosen invariant differential (cf. also Elliptic curve). A similar approach to elliptic genera was used by J. Franke [a3].
Jacobi functions.
Let  be any perfect field of characteristic
be any perfect field of characteristic  and fix an algebraic closure
and fix an algebraic closure  of
of  (cf. Algebraically closed field). Consider a triple
(cf. Algebraically closed field). Consider a triple  consisting of:
consisting of:
i) an elliptic curve  over
over  , i.e. a smooth curve of genus
, i.e. a smooth curve of genus  with a specified
with a specified 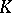 -rational base-point
-rational base-point  ;
;
ii) an invariant 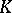 -rational differential
-rational differential  ;
;
iii) a 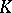 -rational primitive
-rational primitive  -division point
-division point 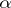 . Following J.I. Igusa [a6] (up to a point), one can associate to these data two functions,
. Following J.I. Igusa [a6] (up to a point), one can associate to these data two functions,  and
and 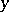 , as follows.
, as follows.
The set  of
of  -division points on
-division points on 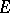 can be described as follows. There are four
can be described as follows. There are four  -division points
-division points  (
(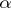 is one of them), four primitive
is one of them), four primitive 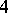 -division points
-division points  such that
such that 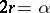 , and eight primitive
, and eight primitive 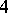 -division points
-division points  such that
such that  . Consider the degree-
. Consider the degree- divisor
divisor 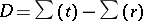 . Since
. Since  in
in  and since Galois symmetries transform
and since Galois symmetries transform  into itself, Abel's theorem (cf., for example, [a11], III.3.5.1, or Abel theorem) implies that there is a function
into itself, Abel's theorem (cf., for example, [a11], III.3.5.1, or Abel theorem) implies that there is a function  , uniquely defined up to a multiplicative constant, such that
, uniquely defined up to a multiplicative constant, such that 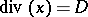 .
.
The function  is odd, satisfies
is odd, satisfies  , and undergoes sign changes under the two other translations of exact order
, and undergoes sign changes under the two other translations of exact order  . Moreover, if
. Moreover, if 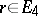 satisfies
satisfies 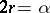 , then translation by
, then translation by  transforms
transforms  into
into 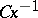 for some non-zero constant
for some non-zero constant  . This constant depends on the choice of
. This constant depends on the choice of  but only up to sign. It follows that
but only up to sign. It follows that 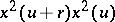 does not depend on the choice of
does not depend on the choice of  . This constant is written as
. This constant is written as  , i.e.
, i.e.
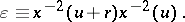 |
One also defines
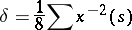 |
(the summation is over the primitive 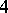 -division points
-division points  such that
such that 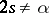 ). If
). If  is one of the values of
is one of the values of  , the other values are
, the other values are  , each taken twice. It follows that
, each taken twice. It follows that
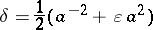 |
and
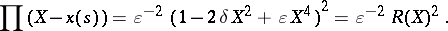 |
It is now easy to see that
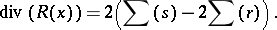 |
Using once more Abel's theorem, one sees that there is a unique 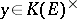 such that
such that 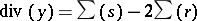 , and
, and 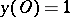 . Since
. Since  , one has
, one has 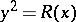 .
.
The differential  has four double poles
has four double poles  . Also, it is easy to see that
. Also, it is easy to see that  is a double zero of
is a double zero of  , hence a simple zero of
, hence a simple zero of  . One concludes that
. One concludes that
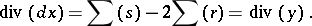 |
and that  is an invariant differential on
is an invariant differential on 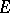 .
.
A slight modification of the argument given in [a6] shows that the Jacobi elliptic functions satisfy the Euler addition formula
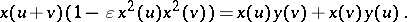 |
Accordingly, one defines the Euler formal group law  by
by
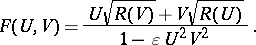 |
Notice that since 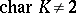 ,
,  is defined over
is defined over 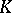 .
.
The elliptic genus.
At this point, one normalizes  over
over  by requiring that
by requiring that  (the given invariant differential). All the objects
(the given invariant differential). All the objects  , and
, and 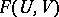 are now completely determined by the initial data. Replacing
are now completely determined by the initial data. Replacing  by
by 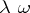 (
(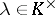 ) yields:
) yields:
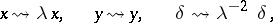 | (a1) |
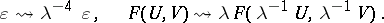 |
As any formal group law,  is classified by a unique ring homomorphism
is classified by a unique ring homomorphism
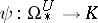 |
from the complex cobordism ring. Since 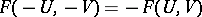 , it is easy to see that
, it is easy to see that  uniquely factors through a ring homomorphism
uniquely factors through a ring homomorphism
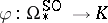 |
from the oriented cobordism ring. By definition, 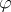 is the level-
is the level- elliptic genus. Suppose now that
elliptic genus. Suppose now that 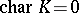 . Define a local parameter
. Define a local parameter  near
near  so that
so that  and
and  . Then
. Then  can be expanded into a formal power series
can be expanded into a formal power series 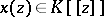 which clearly satisfies
which clearly satisfies 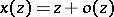 and
and  . In this case, the elliptic genus can be defined as the Hirzebruch genus (cf. [a4] or [a5]) corresponding to the series
. In this case, the elliptic genus can be defined as the Hirzebruch genus (cf. [a4] or [a5]) corresponding to the series 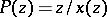 . Since
. Since 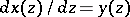 , the logarithm
, the logarithm 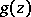 of this elliptic genus is given by the elliptic integral
of this elliptic genus is given by the elliptic integral
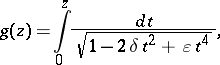 | (a2) |
which gives the original definition in [a9].
Modularity.
For any closed oriented manifold  of dimension
of dimension  ,
, 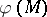 is a function of the triple
is a function of the triple 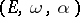 . As easily follows from (a1), multiplying
. As easily follows from (a1), multiplying 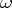 by
by 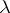 results in multiplying
results in multiplying  by
by 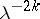 . Also,
. Also,  depends only on the isomorphism class of the triple
depends only on the isomorphism class of the triple  and commutes with arbitrary extensions of the scalar field
and commutes with arbitrary extensions of the scalar field 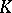 . In the terminology of Katz ([a7]; adapted here to modular forms over fields),
. In the terminology of Katz ([a7]; adapted here to modular forms over fields), 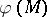 is a modular form of level
is a modular form of level  and weight
and weight  . Let
. Let 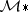 be the graded ring of all such modular forms. Then
be the graded ring of all such modular forms. Then  ,
, 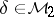 ,
,  . Moreover, one can prove that
. Moreover, one can prove that 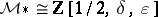 . If one identifies these two isomorphic rings, the elliptic genus becomes the Hirzebruch genus
. If one identifies these two isomorphic rings, the elliptic genus becomes the Hirzebruch genus
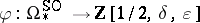 |
with logarithm given by the formal integral (a2).
Integrality.
Consider
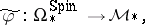 |
i.e., the composition of  with the forgetful homomorphism
with the forgetful homomorphism  . As is shown in [a2],
. As is shown in [a2],
 |
The ring 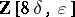 agrees with the ring
agrees with the ring 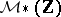 of modular forms over
of modular forms over 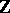 . Thus: If
. Thus: If 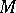 is a
is a 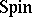 -manifold of dimension
-manifold of dimension 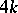 , then
, then 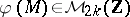 .
.
Example: the Tate curve.
Let 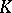 be a local field, complete with respect to a discrete valuation
be a local field, complete with respect to a discrete valuation  , and let
, and let 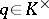 be any element satisfying
be any element satisfying 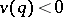 . Consider
. Consider 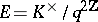 . It is well-known (cf. [a11], § C.14) that
. It is well-known (cf. [a11], § C.14) that 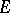 can be identified with the elliptic curve (known as the Tate curve)
can be identified with the elliptic curve (known as the Tate curve)
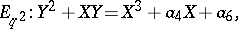 |
where
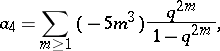 |
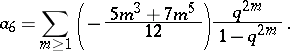 |
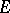 can be treated as an elliptic curve over
can be treated as an elliptic curve over  with
with 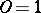 . Fix the invariant differential
. Fix the invariant differential  (
( ) on
) on  (
(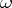 corresponds to the differential
corresponds to the differential 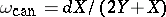 on the Tate curve).
on the Tate curve). 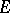 has three
has three  -rational primitive
-rational primitive  -division points:
-division points:  ,
, 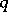 and
and 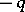 . To describe the corresponding Jacobi function
. To describe the corresponding Jacobi function  , consider the theta-function
, consider the theta-function
 |
This is a "holomorphic" function on  with simple zeros at points of
with simple zeros at points of 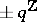 (cf. [a10] for a justification of this terminology), satisfying
(cf. [a10] for a justification of this terminology), satisfying
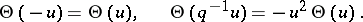 |
Consider the case where 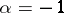 . Let
. Let  be any square root of
be any square root of 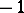 , and let
, and let
 | (a3) |
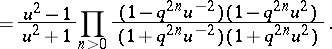 |
 is a meromorphic function on
is a meromorphic function on  satisfying
satisfying 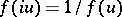 and
and
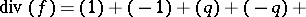 |
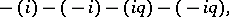 |
i.e., 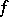 is a multiple of the Jacobi function
is a multiple of the Jacobi function  of
of 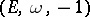 .
.
Notice now that the normalization condition 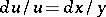 can be written as
can be written as 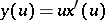 , where
, where 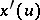 is the derivative with respect to
is the derivative with respect to  . Since
. Since  , one has
, one has 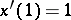 . Differentiating (a3), one obtains
. Differentiating (a3), one obtains
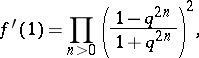 |
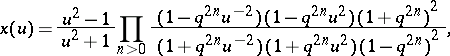 |
and
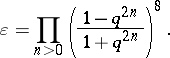 |
Finally, if  , the function
, the function  satisfies
satisfies  . It follows that the generating series
. It follows that the generating series 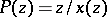 is given by
is given by
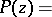 |
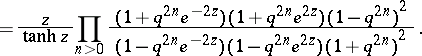 |
The cases where 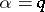 or
or 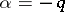 are treated similarly, with
are treated similarly, with
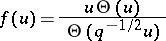 |
and
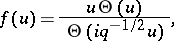 |
respectively.
Strict multiplicativity.
The following theorem, also known (in an equivalent form) as the Witten conjecture, was proven first by C. Taubes [a12], then by R. Bott and Taubes [a1]. Let 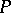 be a principal
be a principal 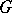 -bundle (cf. also Principal
-bundle (cf. also Principal 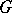 -object) over an oriented manifold
-object) over an oriented manifold 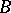 , where
, where 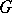 is a compact connected Lie group, and suppose
is a compact connected Lie group, and suppose 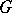 acts on a compact
acts on a compact  -manifold
-manifold 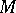 . Then
. Then
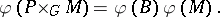 |
For the history of this conjecture, cf. [a8].
References
| [a1] | R. Bott, C. Taubes, "On the rigidity theorems of Witten" J. Amer. Math. Soc. , 2 (1989) pp. 137–186 |
| [a2] | D.V. Chudnovsky, G.V. Chudnovsky, P.S. Landweber, S. Ochanine, R.E. Stong, "Integrality and divisibility of the elliptic genus" Preprint (1988) |
| [a3] | J. Franke, "On the construction of elliptic cohomology" Math. Nachr. , 158 (1992) pp. 43–65 |
| [a4] | F. Hirzebruch, "Topological methods in algebraic geometry" , Grundlehren math. Wiss. , Springer (1966) (Edition: Third) |
| [a5] | F. Hirzebruch, Th. Berger, R. Jung, "Manifolds and modular forms" , Aspects of Mathematics , E20 , Vieweg (1992) (Appendices by Nils-Peter Skoruppa and by Paul Baum) |
| [a6] | J.-I. Igusa, "On the transformation theory of elliptic functions" Amer. J. Math. , 81 (1959) pp. 436–452 |
| [a7] | N.M. Katz, " -adic properties of modular schemes and modular forms" W. Kuyk (ed.) J.-P. Serre (ed.) , Modular Functions in One Variable III. Proc. Internat. Summer School, Univ. of Antwerp, RUCA, July 17--August 3, 1972 , Lecture Notes in Mathematics , 350 (1973) pp. 69–190 -adic properties of modular schemes and modular forms" W. Kuyk (ed.) J.-P. Serre (ed.) , Modular Functions in One Variable III. Proc. Internat. Summer School, Univ. of Antwerp, RUCA, July 17--August 3, 1972 , Lecture Notes in Mathematics , 350 (1973) pp. 69–190 |
| [a8] | P.S. Landweber, "Elliptic genera: An introductory overview" P.S. Landweber (ed.) , Elliptic Curves and Modular Forms in Algebraic Topology (Proc., Princeton 1986) , Lecture Notes in Mathematics , 1326 , Springer (1988) pp. 1–10 |
| [a9] | S. Ochanine, "Sur les genres multiplicatifs définis par des intégrales elliptiques" Topology , 26 (1987) pp. 143–151 |
| [a10] | P. Roquette, "Analytic theory of elliptic functions over local fields" , Hamburger Math. Einzelschrift. , 1 , Vandenhoeck and Ruprecht (1970) |
| [a11] | J.H. Silverman, "The arithmetic of elliptic curves" , GTM , 106 , Springer (1986) |
| [a12] | C. Taubes, "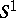 actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 |
Elliptic genera. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elliptic_genera&oldid=12287