Elementary number theory
The branch of number theory that investigates properties of the integers by elementary methods. These methods include the use of divisibility properties, various forms of the axiom of induction and combinatorial arguments. Sometimes the notion of elementary methods is extended by bringing in the simplest elements of mathematical analysis. Traditionally, proofs are deemed to be non-elementary if they involve complex numbers.
Usually, one refers to elementary number theory the problems that arise in branches of number theory such as the theory of divisibility, of congruences, of arithmetic functions, of indefinite equations, of partitions, of additive representations, of the approximation by rational numbers, and of continued fractions. Quite often, the solution of such problems leads to the need to go beyond the framework of elementary methods. Occasionally, following the discovery of a non-elementary solution of some problem, one also finds an elementary solution of it.
As a rule, the problems of elementary number theory have a history going back over centuries, and they are quite often a source of modern trends in number theory and algebra.
From preserved ancient Babylonian cuneiform tablets one may deduce that the Babyloneans were familiar with the task of factoring natural numbers into prime factors. In the 5th century B.C. the Pythagoreans established the so-called doctrine of even and odd numbers and justified the proposition that the product of two natural numbers is even if and only if at least one of the factors is even. A general theory of divisibility was created, in essence, by Euclid. In his Elements (3rd century B.C.), he introduces an algorithm for finding the greatest common divisor of two integers and on this basis he justifies the main theorem of the arithmetic of integers: Every natural number can be factored in one and only one way into a product of prime factors.
After C.F. Gauss, at the beginning of the 19th century, constructed a theory of divisibility of complex integers, it became clear that the study of an arbitrary ring must begin with the construction of a divisibility theory in it.
All properties of the integers are connected in one way or another with the prime numbers (cf. Prime number). Therefore, questions on the disposition of the prime numbers in the sequence of natural numbers evoked the interest of scholars. The first proof that the set of prime numbers is infinite is due to Euclid. Only in the middle of the 19th century did P.L. Chebyshev take the following step in the study of the function 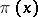 , the number of prime numbers not exceeding
, the number of prime numbers not exceeding  . He succeeded in proving by elementary means inequalities that imply
. He succeeded in proving by elementary means inequalities that imply
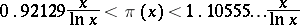 |
for all sufficiently large  . Actually,
. Actually, 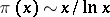 , but this was not established until the end of the 19th century by means of complex analysis. For a long time it was considered impossible to obtain the result by elementary means. However, in 1949, A. Selberg obtained an elementary proof of this theorem. Chebyshev also proved that for
, but this was not established until the end of the 19th century by means of complex analysis. For a long time it was considered impossible to obtain the result by elementary means. However, in 1949, A. Selberg obtained an elementary proof of this theorem. Chebyshev also proved that for 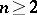 the interval
the interval 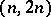 contains at least one prime number. A refinement of the interval containing at least one prime number requires a deeper study of the behaviour of the function
contains at least one prime number. A refinement of the interval containing at least one prime number requires a deeper study of the behaviour of the function 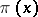 .
.
In the 3rd century B.C. the sieve of Eratosthenes (cf. Eratosthenes, sieve of) was used to select the prime numbers from the set of natural numbers. In 1918 V. Brun showed that a modification of this method can serve as a basis for the study of a set of "almost primes" . He proved the Brun theorem on prime twins. The Brun sieve is a special case of general sieve methods (cf. Sieve method) which give estimates for collections of almost primes not exceeding  and belonging to a sequence
and belonging to a sequence 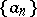 of natural numbers. Sieve methods can be used when "good" approximations in the mean are known for the amount of integers
of natural numbers. Sieve methods can be used when "good" approximations in the mean are known for the amount of integers 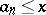 belonging to a progression the modulus of which grows with
belonging to a progression the modulus of which grows with  . Among the sieve methods developed after Brun, the Selberg sieve is of special significance. The strongest results are obtained by a combination of sieve methods and analytic methods. A sieve method in conjunction with the Shnirel'man method made it possible to effectively find a number
. Among the sieve methods developed after Brun, the Selberg sieve is of special significance. The strongest results are obtained by a combination of sieve methods and analytic methods. A sieve method in conjunction with the Shnirel'man method made it possible to effectively find a number 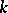 such that any natural number
such that any natural number 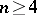 can be represented as a sum of at most
can be represented as a sum of at most 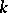 prime numbers.
prime numbers.
Two integers  and
and 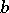 are said to be congruent modulo
are said to be congruent modulo 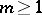 if they have the same remainder on division by
if they have the same remainder on division by 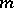 . Gauss (in 1801) introduced the notation
. Gauss (in 1801) introduced the notation 
 . This form of writing, which brings about the analogy of congruences and equations, turned out to be convenient and instrumental in the development of the theory congruences (cf. Congruence).
. This form of writing, which brings about the analogy of congruences and equations, turned out to be convenient and instrumental in the development of the theory congruences (cf. Congruence).
Many results obtained previously by P. Fermat, L. Euler, J.L. Lagrange, and others, and also the Chinese remainder theorem, can be stated and proved simply in the language of the theory of congruences. One of the most interesting results of this theory is the quadratic reciprocity law.
The ancient Babylonians knew a large number of "Pythagorean triples" . Apparently they knew some method for finding arbitrary many integer solutions of the indeterminate equation 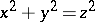 . The Pythagoreans used the formulas
. The Pythagoreans used the formulas 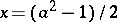 ,
, 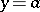 ,
, 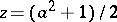 to find solutions of this equation. Euclid indicated a method that allows one to find in succession integer solutions of the equation
to find solutions of this equation. Euclid indicated a method that allows one to find in succession integer solutions of the equation 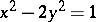 (a special case of the Pell equation). In his Aritmetika Diophantus (3rd century B.C.) made an attempt to setting up a theory of indeterminate equations (see Diophantine equations). In particular, for the solution of equations of the second and some higher degrees he used systematically a device that enabled him to find from one rational solution of a given equation other rational solutions of it. Fermat (17th century) discovered another method, the "method of descent" , and solved by it a number of equations, but the so-called Fermat great theorem, which he declared to have solved, has turned out to be beyond the power of elementary methods.
(a special case of the Pell equation). In his Aritmetika Diophantus (3rd century B.C.) made an attempt to setting up a theory of indeterminate equations (see Diophantine equations). In particular, for the solution of equations of the second and some higher degrees he used systematically a device that enabled him to find from one rational solution of a given equation other rational solutions of it. Fermat (17th century) discovered another method, the "method of descent" , and solved by it a number of equations, but the so-called Fermat great theorem, which he declared to have solved, has turned out to be beyond the power of elementary methods.
Fermat solved the problem of representing natural numbers by sums of two squares of integers. As a result of research by Lagrange (1773) and Gauss (1801) the problem of the representation of integers by a definite binary quadratic form was solved. Gauss developed the general theory of binary quadratic forms. The solution of the problem of representing numbers by forms of higher degree (for example, the Waring problem) and by quadratic forms in several variables usually go beyond the framework of elementary methods. Only certain special cases of such problems can be solved elementarily. An example is Lagrange's theorem: Every natural number is the sum of four squares of integers. It should be mentioned that Diophantus in his Aritmetika repeatedly used the possibility of representing a natural number as the sum of four squares of integers.
To elementary number theory one also reckons the theory of partitions, the foundations of which were laid by Euler (in 1751). One of the basic problems of the theory of partitions is the study of the function 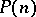 , the number of representations of a natural number
, the number of representations of a natural number  as a sum of natural numbers. Other functions of similar type are also treated in the theory of partitions. Continued fractions (cf. Continued fraction) appeared in connection with problems of approximate computations (extraction of the square root of a natural number, search for approximations of real numbers by common fractions with small denominators). Continued fractions are applied in solving indefinite equations of the first and second degree. Using the apparatus of continued fractions J. Lambert (1766) was the first to establish that the number
as a sum of natural numbers. Other functions of similar type are also treated in the theory of partitions. Continued fractions (cf. Continued fraction) appeared in connection with problems of approximate computations (extraction of the square root of a natural number, search for approximations of real numbers by common fractions with small denominators). Continued fractions are applied in solving indefinite equations of the first and second degree. Using the apparatus of continued fractions J. Lambert (1766) was the first to establish that the number 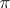 is irrational. In the solution of various problems in the approximation of real numbers by rational numbers one uses in elementary number theory the Dirichlet principle, besides continued fractions.
is irrational. In the solution of various problems in the approximation of real numbers by rational numbers one uses in elementary number theory the Dirichlet principle, besides continued fractions.
In number theory it is easy to state many problems that can be formulated elementarily and have so far remained unsolved. For example; Is the set of even perfect numbers finite or not? Is there at least one odd perfect number? Is the set of Fermat prime numbers finite or not? Is the set of Mersenne prime numbers finite or not (cf. Mersenne number)? Is the set of prime numbers of the form 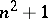 finite or not? Is it true that there is at least one prime number between the squares of two consecutive natural numbers? Is the set of incomplete fractions of the expansion of
finite or not? Is it true that there is at least one prime number between the squares of two consecutive natural numbers? Is the set of incomplete fractions of the expansion of 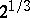 into a continued fraction bounded or not?
into a continued fraction bounded or not?
References
| [1] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [2] | I.M. Vinogradov, "Basic number theory" , Moscow (1981) (In Russian) |
| [3] | A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian) |
| [4] | A.Ya. Khinchin, "Continued fractions" , Univ. Chicago Press (1964) (Translated from Russian) |
| [5] | C.F. Gauss, "Disquisitiones Arithmeticae" , Teubner (1801) (Translated from Latin) |
| [6] | H. Davenport, "The higher arithmetic" , Hutchinson (1952) |
| [7] | E. Trost, "Primzahlen" , Birkhäuser (1953) |
| [8] | G.E. Andrews, "Theory of partitions" , Addison-Wesley (1976) |
| [9] | , The history of mathematics from Antiquity to the beginning of the XIX-th century , 1–3 , Moscow (1970–1972) (In Russian) |
| [10] | H. Wieleitner, "Die Geschichte der Mathematik von Descartes bis zum Hälfte des 19. Jahrhunderts" , de Gruyter (1923) |
| [11] | L.E. Dickson, "History of the theory of numbers" , 1–3 , Chelsea, reprint (1971) |
| [12] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
| [13] | W. Sierpiński, "Elementary theory of numbers" , PWN (1964) (Translated from Polish) |
| [14] | K. Ireland, M. Rosen, "A classical introduction to modern number theory" , Springer (1982) |
Comments
A translation of [5] into English is [a1].
For Chebyshev's result mentioned above see also Chebyshev theorems on prime numbers.
A Pythagorean triple is a triple 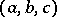 of natural numbers satisfying
of natural numbers satisfying 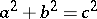 (cf. also Pythagorean numbers).
(cf. also Pythagorean numbers).
For representations of numbers by special (quadratic) forms see also Quadratic form; Goldbach problem. More on partitions can be found in Combinatorial analysis.
Concerning the questions stated at the end of the main article above see also Perfect number; Prime number; Twins.
Fermat numbers are the special case of Mersenne numbers, which are of the form 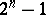 , when
, when  itself is of the form
itself is of the form 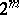 (cf. Mersenne number); here
(cf. Mersenne number); here  ,
,  are natural numbers.
are natural numbers.
References
| [a1] | C.F. Gauss, "Disquisitiones Arithmeticae" , Yale Univ. Press (1966) (Translated from Latin) |
| [a2] | D. Shanks, "Solved and unsolved problems in number theory" , Chelsea, reprint (1978) |
| [a3] | A. Weil, "Number theory: an approach through history: from Hammupari to Legendre" , Birkhäuser (1984) |
Elementary number theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_number_theory&oldid=13948