Disconjugacy
An  th order homogeneous linear differential operator (equation)
th order homogeneous linear differential operator (equation)
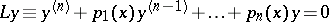 | (a1) |
is called disconjugate on an interval 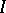 if no non-trivial solution has
if no non-trivial solution has  zeros on
zeros on  , multiple zeros being counted according to their multiplicity. (In the Russian literature this is called non-oscillation on
, multiple zeros being counted according to their multiplicity. (In the Russian literature this is called non-oscillation on  ; cf. also Oscillating solution; Oscillating differential equation.) If (a1) has a solution with
; cf. also Oscillating solution; Oscillating differential equation.) If (a1) has a solution with  zeros on an interval, then the infimum of all values
zeros on an interval, then the infimum of all values  ,
, 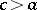 , such that some solution has
, such that some solution has  zeros on
zeros on 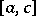 is called the conjugate point of
is called the conjugate point of  and is denoted by
and is denoted by 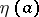 . This infimum is achieved by a solution which has a total of at least
. This infimum is achieved by a solution which has a total of at least  zeros at
zeros at  and
and 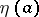 and is positive on
and is positive on 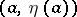 . If the equation has continuous coefficients, the conjugate point
. If the equation has continuous coefficients, the conjugate point 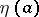 is a strictly increasing, continuous function of
is a strictly increasing, continuous function of  . The adjoint equation has the same conjugate point as (a1). For general properties, see [a1], [a7].
. The adjoint equation has the same conjugate point as (a1). For general properties, see [a1], [a7].
There are numerous explicit sufficient criteria for the equation (a1) to be disconjugate. Many of them are of the form
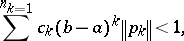 |
where 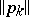 is some norm of
is some norm of 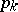 ,
, 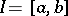 and
and 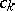 are suitable constants. These are "smallness conditions" which express the proximity of (a1) to the disconjugate equation
are suitable constants. These are "smallness conditions" which express the proximity of (a1) to the disconjugate equation 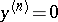 . See [a12].
. See [a12].
 is disconjugate on
is disconjugate on 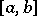 if and only if it has there the Pólya factorization
if and only if it has there the Pólya factorization
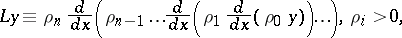 |
or the equivalent Mammana factorization
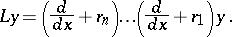 |
Among the various Pólya factorizations, the most important is the Trench canonical form [a11]: If 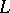 is disconjugate on
is disconjugate on 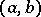 ,
, 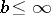 , then there is essentially one factorization such that
, then there is essentially one factorization such that 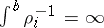 ,
, 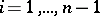 .
.
Disconjugacy is closely related to solvability of the de la Vallée-Poussin multiple-point problem 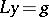 ,
, 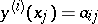 ,
, 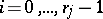 ,
, 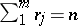 . The Green's function of a disconjugate operator
. The Green's function of a disconjugate operator 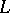 and the related homogeneous boundary value problem satisfies
and the related homogeneous boundary value problem satisfies
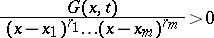 |
for 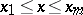 ,
, 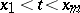 [a7]. Another interesting boundary value problem is the focal boundary value problem
[a7]. Another interesting boundary value problem is the focal boundary value problem 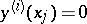 ,
, 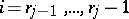 ,
, 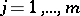 ,
, 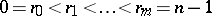 .
.
For a second-order equation, the Sturm separation theorem (cf. Sturm theorem) yields that non-oscillation (i.e., no solution has a sequence of zeros converging to 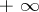 ) implies that there exists a point
) implies that there exists a point  such that (a1) is disconjugate on
such that (a1) is disconjugate on 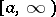 . For equations of order
. For equations of order 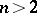 this conclusion holds for a class of equations [a2] but not for all equations [a4].
this conclusion holds for a class of equations [a2] but not for all equations [a4].
Particular results about disconjugacy exist for various special types of differential equations.
1) The Sturm–Liouville operator (cf. Sturm–Liouville equation)
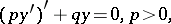 | (a2) |
has been studied using the Sturm (and Sturm–Picone) comparison theorem, the Prüfer transformation and the Riccati equation 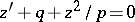 . It is also closely related to the positive definiteness of the quadratic functional
. It is also closely related to the positive definiteness of the quadratic functional 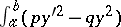 . See [a10], [a1], [a5]. For example, (a2) is disconjugate on
. See [a10], [a1], [a5]. For example, (a2) is disconjugate on 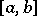 if
if 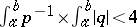 .
.
2) Third-order equations are studied in [a3].
3) For a self-adjoint differential equation 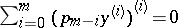 , the existence of a solution with two zeros of multiplicity
, the existence of a solution with two zeros of multiplicity 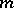 has been studied. Their absence is called
has been studied. Their absence is called 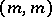 -disconjugacy.
-disconjugacy.
4) Disconjugacy of the analytic equation 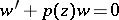 in a complex domain is connected to the theory of univalent functions. See [a8], [a5] and Univalent function.
in a complex domain is connected to the theory of univalent functions. See [a8], [a5] and Univalent function.
5) Many particularly elegant result are available for two-term equations 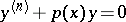 and their generalizations
and their generalizations 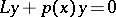 [a6], [a2].
[a6], [a2].
Disconjugacy has also been studied for certain second-order linear differential systems of higher dimension [a1], [a9]. In the historical prologue of [a9], the connection to the calculus of variations (cf. also Variational calculus) is explained. The concepts of disconjugacy and oscillation have also been generalized to non-linear differential equations and functional-differential equations.
References
| [a1] | W.A. Coppel, "Disconjugacy" , Lecture Notes in Mathematics , 220 , Springer (1971) |
| [a2] | U. Elias, "Oscillation theory of two-term differential equations" , Kluwer Acad. Publ. (1997) |
| [a3] | M. Gregus, "Third order linear differential equations" , Reidel (1987) |
| [a4] | Gustafson, G. B., "The nonequivalence of oscillation and nondisconjugacy" Proc. Amer. Math. Soc. , 25 (1970) pp. 254–260 |
| [a5] | E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1968) |
| [a6] | I.T. Kiguradze, T.A. Chanturia, "Asymptotic properties of solutions of nonautonomous ordinary differential equations" , Kluwer Acad. Publ. (1993) (In Russian) |
| [a7] | A.Yu. Levin, "Non-oscillation of solutions of the equation 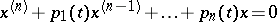 " Russian Math. Surveys , 24 (1969) pp. 43–99 (In Russian) " Russian Math. Surveys , 24 (1969) pp. 43–99 (In Russian) |
| [a8] | Z. Nehari, "The Schwarzian derivative and schlicht functions" Bull. Amer. Math. Soc. , 55 (1949) pp. 545–551 |
| [a9] | W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980) |
| [a10] | C.A. Swanson, "Comparison and oscillatory theory of linear differential equations" , Acad. Press (1968) |
| [a11] | W.F. Trench, "Canonical forms and principal systems for general disconjugate equation" Trans. Amer. Math. Soc. , 189 (1974) pp. 319–327 |
| [a12] | D. Willet, "Generalized de la Vallée Poussin disconjugacy tests for linear differential equations" Canadian Math. Bull. , 14 (1971) pp. 419–428 |
Disconjugacy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Disconjugacy&oldid=18945