Difference between revisions of "Direct product"
(MSC 03E) |
(mention restricted direct product) |
||
| Line 17: | Line 17: | ||
The value of a predicate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273040.png" /> is true if for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273041.png" /> the value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273042.png" /> is true. Moreover, if in all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273043.png" /> an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively. | The value of a predicate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273040.png" /> is true if for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273041.png" /> the value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273042.png" /> is true. Moreover, if in all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273043.png" /> an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively. | ||
| − | For an arbitrary factor of a direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273044.png" /> there exists a natural projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273045.png" />, defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273046.png" />. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273047.png" /> and the family of projections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273049.png" />, have the following universal property: For every family of mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273050.png" /> there exists a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273051.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273052.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273053.png" />. This property also holds if all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273054.png" /> are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the [[ | + | For an arbitrary factor of a direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273044.png" /> there exists a natural projection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273045.png" />, defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273046.png" />. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273047.png" /> and the family of projections <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273049.png" />, have the following universal property: For every family of mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273050.png" /> there exists a unique mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273051.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273052.png" /> for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273053.png" />. This property also holds if all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d032/d032730/d03273054.png" /> are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the [[product of a family of objects in a category]]. |
One often encounters problems of describing mathematical objects that cannot be decomposed into a direct product, and of stating conditions under which the factors of a direct product are uniquely determined up to an isomorphism. Classical results in this respect are the theorem on the structure of finitely-generated modules over principal ideal rings and the Remak–Schmidt theorem on the central isomorphism of direct decompositions of a group with a principal series. | One often encounters problems of describing mathematical objects that cannot be decomposed into a direct product, and of stating conditions under which the factors of a direct product are uniquely determined up to an isomorphism. Classical results in this respect are the theorem on the structure of finitely-generated modules over principal ideal rings and the Remak–Schmidt theorem on the central isomorphism of direct decompositions of a group with a principal series. | ||
| − | The direct product is sometimes called the complete direct product, to distinguish it from the discrete direct product (or [[ | + | The direct product is sometimes called the complete direct product, to distinguish it from the [[restricted direct product]], which is defined when there is a supplementary structure in the factors: an important case of this is the discrete direct product (or [[direct sum]]), which is defined when the supplementary structures are a one-element substructures (e.g. base points of [[pointed set]]s and [[pointed space]]s, unit subgroups of groups, zero subspaces, etc.). As a rule, the direct product of a finite number of factors coincides with the discrete product. |
Revision as of 17:58, 22 November 2014
2020 Mathematics Subject Classification: Primary: 03E [MSN][ZBL]
A basic general mathematical construction. The idea behind it is due to R. Descartes; therefore the direct product is also called the Cartesian product. The direct product, or simply the product, of two non-empty sets 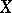 and
and 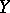 is the set
is the set 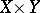 consisting of all ordered pairs of the form
consisting of all ordered pairs of the form 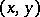 ,
, 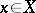 ,
, 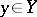 :
:
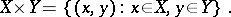 |
If one of the sets 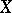 or
or 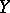 is empty then so is their product. The set
is empty then so is their product. The set 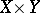 can be identified with the set of functions defined on the two-element set
can be identified with the set of functions defined on the two-element set 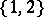 and taking the value 1 for elements of
and taking the value 1 for elements of 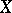 , and the value 2 for elements of
, and the value 2 for elements of  . This identification leads to a general definition of a direct product of sets. Let
. This identification leads to a general definition of a direct product of sets. Let 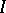 be some index set and suppose that
be some index set and suppose that 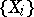 is an arbitrary family of sets, indexed by the elements of
is an arbitrary family of sets, indexed by the elements of 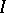 . The direct product of the
. The direct product of the 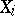 ,
,  , is the set of functions
, is the set of functions 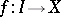 , where
, where 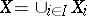 , such that
, such that 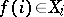 for every
for every 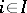 . Usually, the direct product is denoted by
. Usually, the direct product is denoted by 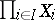 , for a finite index set
, for a finite index set 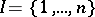 one also uses the notations
one also uses the notations 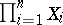 and
and 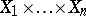 . If
. If 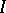 consists of the single element 1, then
consists of the single element 1, then 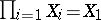 . Sometimes one defines the direct product of a finite number of factors inductively:
. Sometimes one defines the direct product of a finite number of factors inductively:
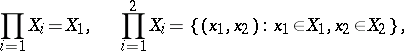 |
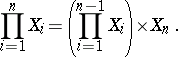 |
One merit of the construction of a direct product rests above all in the possibility of naturally introducing supplementary structures in it, if all factors have the same mathematical structure. E.g., if the  ,
, 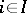 , are algebraic systems of the same type, i.e. sets with a common signature of finitely-placed predicates and operations, then the product
, are algebraic systems of the same type, i.e. sets with a common signature of finitely-placed predicates and operations, then the product 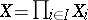 can be made into an algebraic system of the same signature: For functions
can be made into an algebraic system of the same signature: For functions 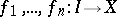 and an
and an  -ary operation
-ary operation 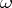 the action of the function
the action of the function 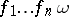 on one element
on one element 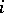 is defined by
is defined by
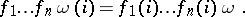 |
The value of a predicate  is true if for every
is true if for every 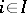 the value of
the value of 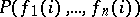 is true. Moreover, if in all
is true. Moreover, if in all 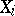 an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively.
an equation is satisfied, then it is also satisfied in their product. Therefore, the product of semi-groups, groups, rings, vector spaces, etc., is again a semi-group, group, ring, vector space, respectively.
For an arbitrary factor of a direct product  there exists a natural projection
there exists a natural projection  , defined by
, defined by 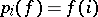 . The set
. The set 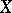 and the family of projections
and the family of projections 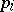 ,
, 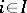 , have the following universal property: For every family of mappings
, have the following universal property: For every family of mappings 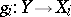 there exists a unique mapping
there exists a unique mapping  such that
such that  for every
for every 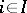 . This property also holds if all
. This property also holds if all  are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the product of a family of objects in a category.
are algebraic systems of one type, and makes it possible to define a suitable topology on a direct product of topological spaces. The property formulated is the basis for the definition of the product of a family of objects in a category.
One often encounters problems of describing mathematical objects that cannot be decomposed into a direct product, and of stating conditions under which the factors of a direct product are uniquely determined up to an isomorphism. Classical results in this respect are the theorem on the structure of finitely-generated modules over principal ideal rings and the Remak–Schmidt theorem on the central isomorphism of direct decompositions of a group with a principal series.
The direct product is sometimes called the complete direct product, to distinguish it from the restricted direct product, which is defined when there is a supplementary structure in the factors: an important case of this is the discrete direct product (or direct sum), which is defined when the supplementary structures are a one-element substructures (e.g. base points of pointed sets and pointed spaces, unit subgroups of groups, zero subspaces, etc.). As a rule, the direct product of a finite number of factors coincides with the discrete product.
Direct product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Direct_product&oldid=34810