Differential calculus
A branch of mathematics dealing with the concepts of derivative and differential and the manner of using them in the study of functions. The development of differential calculus is closely connected with that of integral calculus. Indissoluble is also their content. Together they form the base of mathematical analysis, which is extremely important in the natural sciences and in technology. The introduction of variable magnitudes into mathematics by R. Descartes was the principal factor in the creation of differential calculus. Differential and integral calculus were created, in general terms, by I. Newton and G. Leibniz towards the end of the 17th century, but their justification by the concept of limit was only developed in the work of A.L. Cauchy in the early 19th century. The creation of differential and integral calculus initiated a period of rapid development in mathematics and in related applied disciplines. Differential calculus is usually understood to mean classical differential calculus, which deals with real-valued functions of one or more real variables, but its modern definition may also include differential calculus in abstract spaces. Differential calculus is based on the concepts of real number; function; limit and continuity — highly important mathematical concepts, which were formulated and assigned their modern content during the development of mathematical analysis and during studies of its foundations. The central concepts of differential calculus — the derivative and the differential — and the apparatus developed in this connection furnish tools for the study of functions which locally look like linear functions or polynomials, and it is in fact such functions which are of interest, more than other functions, in applications.
Derivative.
Let a function $ y = f ( x) $ be defined in some neighbourhood of a point $ x _ {0} $. Let $ \Delta x \neq 0 $ denote the increment of the argument and let $ \Delta y = f ( x _ {0} + \Delta x ) - f ( x _ {0} ) $ denote the corresponding increment of the value of the function. If there exists a (finite or infinite) limit
$$ \lim\limits _ {\Delta x \rightarrow 0 } \frac{\Delta y }{\Delta x } , $$
then this limit is said to be the derivative of the function $ f $ at $ x _ {0} $; it is denoted by $ f ^ { \prime } ( x _ {0} ) $, $ df ( x _ {0} ) / dx $, $ y ^ \prime $, $ y _ {x} ^ \prime $, $ dy / dx $. Thus, by definition,
$$ f ^ { \prime } ( x _ {0} ) = \lim\limits _ {\Delta x \rightarrow 0 } \ \frac{\Delta y }{\Delta x } = \lim\limits _ {\Delta x \rightarrow 0 } \ \frac{f ( x _ {0} + \Delta x ) - f ( x _ {0} ) }{\Delta x } . $$
The operation of calculating the derivative is called differentiation. If $ f ^ { \prime } ( x _ {0} ) $ is finite, the function $ f $ is called differentiable at the point $ x _ {0} $. A function which is differentiable at each point of some interval is called differentiable in the interval.
Geometric interpretation of the derivative.
Let $ C $ be the plane curve defined in an orthogonal coordinate system by the equation $ y = f ( x) $ where $ f $ is defined and is continuous in some interval $ J $; let $ M ( x _ {0} , y _ {0} ) $ be a fixed point on $ C $, let $ P ( x , y ) $( $ x \in J $) be an arbitrary point of the curve $ C $ and let $ MP $ be the secant (Fig. a). An oriented straight line $ MT $( $ T $ a variable point with abscissa $ x _ {0} + \Delta x $) is called the tangent to the curve $ C $ at the point $ M $ if the angle $ \phi $ between the secant $ MP $ and the oriented straight line tends to zero as $ x \rightarrow x _ {0} $( in other words, as the point $ P \in C $ arbitrarily tends to the point $ M $). If such a tangent exists, it is unique. Putting $ x = x _ {0} + \Delta x $, $ \Delta y = f ( x _ {0} + \Delta x ) - f ( x _ {0} ) $, one obtains the equation $ \mathop{\rm tan} \beta = \Delta y / \Delta x $ for the angle $ \beta $ between $ MP $ and the positive direction of the $ x $- axis (Fig. a).
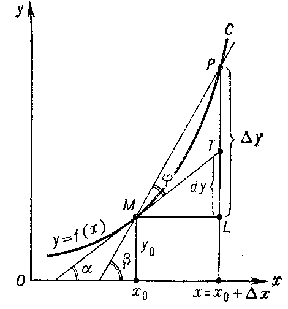
Figure: d031850a
The curve $ C $ has a tangent at the point $ M $ if and only if $ \lim\limits _ {\Delta x \rightarrow 0 } \Delta y / \Delta x $ exists, i.e. if $ f ^ { \prime } ( x _ {0} ) $ exists. The equation $ \mathop{\rm tan} \alpha = f ^ { \prime } ( x _ {0} ) $ is valid for the angle $ \alpha $ between the tangent and the positive direction of the $ x $- axis. If $ f ^ { \prime } ( x _ {0} ) $ is finite, the tangent forms an acute angle with the positive $ x $- axis, i.e. $ - \pi / 2 < \alpha < \pi / 2 $; if $ f ^ { \prime } ( x _ {0} ) = \infty $, the tangent forms a right angle with that axis (cf. Fig. b).
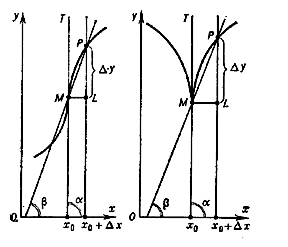
Figure: d031850b
Thus, the derivative of a continuous function $ f $ at a point $ x _ {0} $ is identical to the slope $ \mathop{\rm tan} \alpha $ of the tangent to the curve defined by the equation $ y = f ( x) $ at its point with abscissa $ x _ {0} $.
Mechanical interpretation of the derivative.
Let a point $ M $ move in a straight line in accordance with the law $ s = f ( t) $. During time $ \Delta t $ the point $ M $ becomes displaced by $ \Delta s = f ( t + \Delta t ) - f ( t) $. The ratio $ \Delta s / \Delta t $ represents the average velocity $ v _ { \mathop{\rm av} } $ during the time $ \Delta t $. If the motion is non-uniform, $ v _ { \mathop{\rm av} } $ is not constant. The instantaneous velocity at the moment $ t $ is the limit of the average velocity as $ \Delta t \rightarrow 0 $, i.e. $ v = f ^ { \prime } ( t) $( on the assumption that this derivative in fact exists).
Thus, the concept of derivative constitutes the general solution of the problem of constructing tangents to plane curves, and of the problem of calculating the velocity of a rectilinear motion. These two problems served as the main motivation for formulating the concept of derivative.
A function which has a finite derivative at a point $ x _ {0} $ is continuous at this point. A continuous function need not have a finite nor an infinite derivative. There exist continuous functions having no derivative at any point of their domain of definition.
The formulas given below are valid for the derivatives of the fundamental elementary functions at any point of their domain of definition (exceptions are stated):
1) if $ f ( x) = C = \textrm{ const } $, then $ f ^ { \prime } ( x) = C ^ { \prime } = 0 $;
2) if $ f ( x) = x $, then $ f ^ { \prime } ( x) = 1 $;
3) $ ( x ^ \alpha ) ^ \prime = \alpha x ^ {\alpha - 1 } $, $ \alpha = \textrm{ const } $( $ x \neq 0 $, if $ \alpha \leq 1 $);
4) $ ( \alpha ^ {x} ) ^ \prime = a ^ {x} \mathop{\rm ln} a $, $ a = \textrm{ const } > 0 $, $ a \neq 1 $; in particular, $ ( e ^ {x} ) ^ \prime = e ^ {x} $;
5) $ ( \mathop{\rm log} _ {a} x ) ^ \prime = ( { \mathop{\rm log} _ {a} e } ) / x = 1 / {( x \mathop{\rm ln} a ) } $, $ a = \textrm{ const } > 0 $, $ a \neq 1 $, $ ( \mathop{\rm ln} x ) ^ \prime = 1 / x $;
6) $ ( \sin x ) ^ \prime = \cos x $;
7) $ ( \cos x ) ^ \prime = - \sin x $;
8) $ ( \mathop{\rm tan} x ) ^ \prime = 1 / {\cos ^ {2} x } $;
9) $ ( \mathop{\rm cotan} x ) ^ \prime = - 1 / {\sin ^ {2} x } $;
10) $ ( \mathop{\rm arcsin} x ) ^ \prime = 1 / \sqrt {1 - x ^ {2} } $, $ x \neq \pm 1 $;
11) $ ( \mathop{\rm arccos} x ) ^ \prime = - 1 / \sqrt {1 - x ^ {2} } $, $ x \neq \pm 1 $;
12) $ ( \mathop{\rm arctan} x ) ^ \prime = 1 / ( {1 + x ^ {2} } ) $;
13) $ ( \mathop{\rm arccotan} x ) ^ \prime = - 1 / ( {1 + x ^ {2} } ) $;
14) $ ( \sinh x ) ^ \prime = \cosh x $;
15) $ ( \cosh x ) ^ \prime = \sinh x $;
16) $ ( \mathop{\rm tanh} x ) ^ \prime = 1 / {\cosh ^ {2} x } $;
17) $ ( \mathop{\rm cotanh} x ) ^ \prime = - 1 / {\sinh ^ {2} x } $.
The following laws of differentiation are valid:
If two functions $ u $ and $ v $ are differentiable at a point $ x _ {0} $, then the functions
$$ c u \ ( \textrm{ where } c = \textrm{ const } ) ,\ u \pm v ,\ \ uv ,\ \frac{u}{v} ( v \neq 0 ) $$
are also differentiable at that point, and
$$ ( c u ) ^ \prime = c u ^ \prime , $$
$$ ( u \pm v ) ^ \prime = u ^ \prime \pm v ^ \prime , $$
$$ ( u v ) ^ \prime = u ^ \prime v + u v ^ \prime , $$
$$ \left ( \frac{u}{v} \right ) ^ { \prime } = \frac{u ^ \prime v - u v ^ \prime }{v ^ {2} } . $$
Theorem on the derivative of a composite function: If the function $ y = f ( u) $ is differentiable at a point $ u _ {0} $, while the function $ \phi ( x) $ is differentiable at a point $ x _ {0} $, and if $ u _ {0} = \phi ( x _ {0} ) $, then the composite function $ y = f ( \phi ( x) ) $ is differentiable at $ x _ {0} $, and $ y _ {x} ^ \prime = f ^ { \prime } ( u _ {0} ) \phi ^ \prime ( x _ {0} ) $ or, using another notation, $ dy / dx = ( dy / du ) ( du / dx ) $.
Theorem on the derivative of the inverse function: If $ y = f ( x) $ and $ x = g ( y) $ are two mutually inverse increasing (or decreasing) functions, defined on certain intervals, and if $ f ^ { \prime } ( x _ {0} ) \neq 0 $ exists (i.e. is not infinite), then at the point $ y _ {0} = f ( x _ {0} ) $ the derivative $ g ^ \prime ( y _ {0} ) = 1 / f ^ { \prime } ( x _ {0} ) $ exists, or, in a different notation, $ dx / dy = 1 / ( dy / dx) $. This theorem may be extended: If the other conditions hold and if also $ f ^ { \prime } ( x _ {0} ) = 0 $ or $ f ^ { \prime } ( x _ {0} ) = \infty $, then, respectively, $ g ^ \prime ( y _ {0} ) = \infty $ or $ g ^ \prime ( y _ {0} ) = 0 $.
One-sided derivatives.
If at a point $ x _ {0} $ the limit
$$ \lim\limits _ {\Delta x \downarrow 0 } \ \frac{\Delta y }{\Delta x } $$
exists, it is called the right-hand derivative of the function $ y = f ( x) $ at $ x _ {0} $( in such a case the function need not be defined everywhere in a certain neighbourhood of the point $ x _ {0} $; this requirement may then be restricted to $ x \geq x _ {0} $). The left-hand derivative is defined in the same way, as:
$$ \lim\limits _ {\Delta x \uparrow 0 } \ \frac{\Delta y }{\Delta x } . $$
A function $ f $ has a derivative at a point $ x _ {0} $ if and only if equal right-hand and left-hand derivatives exist at that point. If the function is continuous, the existence of a right-hand (left-hand) derivative at a point is equivalent to the existence, at the corresponding point of its graph, of a right (left) one-sided semi-tangent with slope equal to the value of this one-sided derivative. Points at which the semi-tangents do not form a straight line are called angular points or cusps (cf. Fig. c).
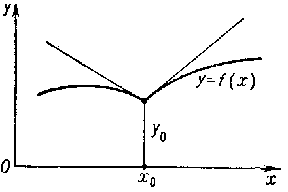
Figure: d031850c
Derivatives of higher orders.
Let a function $ y = f ( x) $ have a finite derivative $ y ^ \prime = f ^ { \prime } ( x) $ at all points of some interval; this derivative is also known as the first derivative, or the derivative of the first order, which, being a function of $ x $, may in its turn have a derivative $ y ^ {\prime\prime} = f ^ { \prime\prime } ( x) $, known as the second derivative, or the derivative of the second order, of the function $ f $, etc. In general, the $ n $- th derivative, or the derivative of order $ n $, is defined by induction by the equation $ y ^ {(} n) = ( y ^ {( n - 1 ) } ) ^ \prime $, on the assumption that $ y ^ {( n - 1 ) } $ is defined on some interval. The notations employed along with $ y ^ {( n) } $ are $ f ^ { ( n) } $, $ d ^ {n} f ( x) / dx ^ {n} $, and, if $ n = 2 , 3 $, also $ y ^ {\prime\prime} $, $ f ^ { \prime\prime } ( x) $, $ y ^ {\prime\prime\prime} $, $ f ^ { \prime\prime\prime } ( x) $.
The second derivative has a mechanical interpretation: It is the acceleration $ w = d ^ {2} s / dt ^ {2} = f ^ { \prime\prime } ( t) $ of a point in rectilinear motion according to the law $ s = f ( t) $.
Differential.
Let a function $ y = f ( x) $ be defined in some neighbourhood of a point $ x $ and let there exist a number $ A $ such that the increment $ \Delta y $ may be represented as $ \Delta y = A \Delta x + \omega $ with $ \omega / \Delta x \rightarrow 0 $ as $ \Delta x \rightarrow 0 $. The term $ A \Delta x $ in this sum is denoted by the symbol $ dy $ or $ df $ and is named the differential of the function $ f ( x) $( with respect to the variable $ x $) at $ x $. The differential is the principal linear part of increment of the function (its geometrical expression is the segment $ LT $ in Fig. a, where $ MT $ is the tangent to $ y = f ( x) $ at the point $ ( x _ {0} , y _ {0} ) $ under consideration).
The function $ y = f ( x) $ has a differential at $ x $ if and only if it has a finite derivative
$$ f ^ { \prime } ( x) = \lim\limits _ {\Delta x \rightarrow 0 } \frac{\Delta y }{\Delta x } = A $$
at this point. A function for which a differential exists is called differentiable at the point in question. Thus, the differentiability of a function implies the existence of both the differential and the finite derivative, and $ dy = df ( x) = f ^ { \prime } ( x) \Delta x $. For the independent variable $ x $ one puts $ dx = \Delta x $, and one may accordingly write $ dy = f ^ { \prime } ( x) dx $, i.e. the derivative is equal to the ratio of the differentials:
$$ f ^ { \prime } ( x) = \frac{dy }{dx } . $$
See also Differential.
The formulas and the rules for computing derivatives lead to corresponding formulas and rules for calculating differentials. In particular, the theorem on the differential of a composite function is valid: If a function $ y = f ( u) $ is differentiable at a point $ u _ {0} $, while a function $ \phi ( x) $ is differentiable at a point $ x _ {0} $ and $ u _ {0} = \phi ( x _ {0} ) $, then the composite function $ y = f ( \phi ( x) ) $ is differentiable at the point $ x _ {0} $ and $ dy = f ^ { \prime } ( u _ {0} ) du $, where $ du = \phi ^ \prime ( x _ {0} ) dx $. The differential of a composite function has exactly the form it would have if the variable $ u $ were an independent variable. This property is known the invariance of the form of the differential. However, if $ u $ is an independent variable, $ du = \Delta u $ is an arbitrary increment, but if $ u $ is a function, $ du $ is the differential of this function which, in general, is not identical with its increment.
Differentials of higher orders.
The differential $ dy $ is also known as the first differential, or differential of the first order. Let $ y = f ( x) $ have a differential $ dy = f ^ { \prime } ( x) dx $ at each point of some interval. Here $ dx = \Delta x $ is some number independent of $ x $ and one may say, therefore, that $ dx = \textrm{ const } $. The differential $ dy $ is a function of $ x $ alone, and may in turn have a differential, known as the second differential, or the differential of the second order, of $ f $, etc. In general, the $ n $- th differential, or the differential of order $ n $, is defined by induction by the equality $ d ^ {n} y = d ( d ^ {n-} 1 y ) $, on the assumption that the differential $ d ^ {n-} 1 y $ is defined on some interval and that the value of $ dx $ is identical at all steps. The invariance condition for $ d ^ {2} y , d ^ {3} y \dots $ is generally not satisfied (with the exception $ y = f ( u) $ where $ u $ is a linear function).
The repeated differential of $ dy $ has the form
$$ \delta ( dy ) = f ^ { \prime\prime } ( x) dx \delta x $$
and the value of $ \delta ( dy) $ for $ dx = \delta x $ is the second differential.
Principal theorems and applications of differential calculus.
The fundamental theorems of differential calculus for functions of a single variable are usually considered to include the Rolle theorem, the Legendre theorem (on finite variation), the Cauchy theorem, and the Taylor formula. These theorems underlie the most important applications of differential calculus to the study of properties of functions — such as increasing and decreasing functions, convex and concave graphs, finding the extrema, points of inflection, and the asymptotes of a graph (cf. Extremum; Point of inflection; Asymptote). Differential calculus makes it possible to compute the limits of a function in many cases when this is not feasible by the simplest limit theorems (cf. Indefinite limits and expressions, evaluations of). Differential calculus is extensively applied in many fields of mathematics, in particular in geometry.
Differential calculus of functions in several variables.
For the sake of simplicity the case of functions in two variables (with certain exceptions) is considered below, but all relevant concepts are readily extended to functions in three or more variables. Let a function $ z = f ( x , y) $ be given in a certain neighbourhood of a point $ ( x _ {0} , y _ {0} ) $ and let the value $ y= y _ {0} $ be fixed. $ f( x, y _ {0} ) $ will then be a function of $ x $ alone. If it has a derivative with respect to $ x $ at $ x _ {0} $, this derivative is called the partial derivative of $ f $ with respect to $ x $ at $ ( x _ {0} , y _ {0} ) $; it is denoted by $ f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) $, $ \partial f ( x _ {0} , y _ {0} ) / \partial x $, $ \partial f / \partial x $, $ z _ {x} ^ \prime $, $ \partial z / \partial x $, or $ f _ {x} ( x _ {0} , y _ {0} ) $. Thus, by definition,
$$ f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) = \lim\limits _ {\Delta x \rightarrow 0 } \frac{\Delta _ {x} z }{\Delta x } = \lim\limits _ {\Delta x \rightarrow 0 } \frac{f ( x _ {0} + \Delta x , y _ {0} ) - f ( x _ {0} , y _ {0} ) }{\Delta x } , $$
where $ \Delta _ {x} z = f ( x _ {0} + \Delta x , y _ {0} ) - f ( x _ {0} , y _ {0} ) $ is the partial increment of the function with respect to $ x $( in the general case, $ \partial z / \partial x $ must not be regarded as a fraction; $ \partial / \partial x $ is the symbol of an operation).
The partial derivative with respect to $ y $ is defined in a similar manner:
$$ f _ {y} ^ { \prime } ( x _ {0} , y _ {0} ) = \lim\limits _ {\Delta y \rightarrow 0 } \frac{\Delta _ {y} z }{\Delta y } = \lim\limits _ {\Delta y \rightarrow 0 } \frac{f ( x _ {0} , y _ {0} + \Delta y ) - f ( x _ {0} , y _ {0} ) }{\Delta y } , $$
where $ \Delta _ {y} z $ is the partial increment of the function with respect to $ y $. Other notations include $ \partial f ( x _ {0} , y _ {0} ) / \partial y $, $ \partial f / \partial y $, $ z _ {y} ^ \prime $, $ \partial z / \partial y $, and $ f _ {y} ( x _ {0} , y _ {0} ) $. Partial derivatives are calculated according to the rules of differentiation of functions of a single variable (in computing $ z _ {x} ^ \prime $ one assumes $ y = \textrm{ const } $ while if $ z _ {y} ^ \prime $ is calculated, one assumes $ x = \textrm{ const } $).
The partial differentials of $ z = f( x, y) $ at $ ( x _ {0} , y _ {0} ) $ are, respectively,
$$ d _ {x} z = f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) dx; \ d _ {y} z = \ f _ {y} ^ { \prime } ( x _ {0} , y _ {0} ) dy , $$
where, as in the case of a single variable, $ dx = \Delta x $, $ dy = \Delta y $ denote the increments of the independent variables.
The first partial derivatives $ \partial z / \partial x = f _ {x} ^ { \prime } ( x, y) $ and $ \partial z / \partial y = f _ {y} ^ { \prime } ( x, y) $, or the partial derivatives of the first order, are functions of $ x $ and $ y $, and may in their turn have partial derivatives with respect to $ x $ and $ y $. These are named, with respect to the function $ z= f( x, y) $, the partial derivatives of the second order, or second partial derivatives. It is assumed that
$$ \frac \partial {\partial x } \left ( \frac{\partial z }{\partial x } \right ) = \frac{\partial ^ {2} z }{\partial x ^ {2} } ,\ \frac \partial {\partial y } \left ( \frac{\partial z }{\partial x } \right ) = \frac{\partial ^ {2} z }{\partial x \partial y } , $$
$$ \frac \partial {\partial x } \left ( \frac{\partial z }{\partial y } \right ) = \frac{\partial ^ {2} z }{\partial y \partial x } ,\ \frac \partial {\partial y } \left ( \frac{\partial z }{\partial y } \right ) = \frac{\partial ^ {2} z }{\partial y ^ {2} } . $$
The following notations are also used instead of $ \partial ^ {2} z / \partial x ^ {2} $:
$$ z _ {xx} ^ {\prime\prime} ,\ z _ {x ^ {2} } ^ {\prime\prime} ,\ \frac{\partial ^ {2} f ( x, y) }{\partial x ^ {2} } ,\ \frac{\partial ^ {2} f }{\partial x ^ {2} } ,\ f _ {xx} ^ { \prime\prime } ( x, y) ,\ f _ {x ^ {2} } ^ { \prime\prime } ( x, y) ,\ f _ {xx} ( x , y ) ; $$
and instead of $ \partial ^ {2} z / \partial x \partial y $:
$$ z _ {xy} ^ {\prime \prime } ,\ \frac{\partial ^ {2} f ( x, y) }{\partial x \partial y } ,\ \ \frac{\partial ^ {2} f }{\partial x \partial y } ,\ f _ {xy} ^ { \prime \prime } ( x, y) ,\ f _ {xy} ( x , y ) , $$
etc. One can introduce in the same manner partial derivatives of the third and higher orders, together with the respective notations: $ \partial ^ {n} z / \partial x ^ {n} $ means that the function $ z $ is to be differentiated $ n $ times with respect to $ x $; $ \partial ^ {n} z / \partial x ^ {p} \partial y ^ {q} $ where $ n = p+ q $ means that the function $ z $ is differentiated $ p $ times with respect to $ x $ and $ q $ times with respect to $ y $. The partial derivatives of second and higher orders obtained by differentiation with respect to different variables are known as mixed partial derivatives.
To each partial derivative corresponds some partial differential, obtained by its multiplication by the differentials of the independent variables taken to the powers equal to the number of differentiations with respect to the respective variable. In this way one obtains the $ n $- th partial differentials, or the partial differentials of order $ n $:
$$ \frac{\partial ^ {n} z }{\partial x ^ {n} } dx ^ {n} ,\ \frac{\partial ^ {n} z }{\partial x ^ {p} \partial y ^ {q} } dx ^ {p} dy ^ {q} . $$
The following important theorem on derivatives is valid: If, in a certain neighbourhood of a point $ ( x _ {0} , y _ {0} ) $, a function $ z = f( x, y) $ has mixed partial derivatives $ f _ {xy} ^ { \prime\prime } ( x, y) $ and $ f _ {yx} ^ { \prime\prime } ( x, y) $, and if these derivatives are continuous at the point $ ( x _ {0} , y _ {0} ) $, then they coincide at this point.
A function $ z = f( x, y) $ is called differentiable at a point $ ( x _ {0} , y _ {0} ) $ with respect to both variables $ x $ and $ y $ if it is defined in some neighbourhood of this point, and if its total increment
$$ \Delta z = f ( x _ {0} + \Delta x, y _ {0} + \Delta y ) - f ( x _ {0} , y _ {0} ) $$
may be represented in the form
$$ \Delta z = A \Delta x + B \Delta y + \omega , $$
where $ A $ and $ B $ are certain numbers and $ \omega / \rho \rightarrow 0 $ for $ \rho = \sqrt {( \Delta x ) ^ {2} + ( \Delta y ) ^ {2} } \rightarrow 0 $( provided that the point $ ( x _ {0} + \Delta x, y _ {0} + \Delta y) $ lies in this neighbourhood). In this context, the expression
$$ dz = df ( x _ {0} , y _ {0} ) = A \Delta x + B \Delta y $$
is called the total differential (of the first order) of $ f $ at $ ( x _ {0} , y _ {0} ) $; this is the principal linear part of increment. A function which is differentiable at a point is continuous at that point (the converse proposition is not always true!). Moreover, differentiability entails the existence of finite partial derivatives
$$ f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) = \lim\limits _ {\Delta x \rightarrow 0 } \frac{\Delta _ {x} z }{\Delta x } = A,\ f _ {y} ^ { \prime } ( x _ {0} , y _ {0} ) = \lim\limits _ {\Delta y \rightarrow 0 } \frac{\Delta _ {y} z }{ \Delta y } = B . $$
Thus, for a function which is differentiable at $ ( x _ {0} , y _ {0} ) $,
$$ dz = df( x _ {0} , y _ {0} ) = f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) \Delta x + f _ {y} ^ { \prime } ( x _ {0} , y _ {0} ) \Delta y , $$
or
$$ dz = df( x _ {0} , y _ {0} ) = f _ {x} ^ { \prime } ( x _ {0} , y _ {0} ) \ dx + f _ {y} ^ { \prime } ( x _ {0} , y _ {0} ) dy , $$
if, as in the case of a single variable, one puts, for the independent variables, $ dx = \Delta x $, $ dy = \Delta y $.
The existence of finite partial derivatives does not, in the general case, entail differentiability (unlike in the case of functions in a single variable). The following is a sufficient criterion of the differentiability of a function in two variables: If, in a certain neighbourhood of a point $ ( x _ {0} , y _ {0} ) $, a function $ f $ has finite partial derivatives $ f _ {x} ^ { \prime } $ and $ f _ {y} ^ { \prime } $ which are continuous at $ ( x _ {0} , y _ {0} ) $, then $ f $ is differentiable at this point. Geometrically, the total differential $ df( x _ {0} , y _ {0} ) $ is the increment of the applicate of the tangent plane to the surface $ z = f( x, y) $ at the point $ ( x _ {0} , y _ {0} , z _ {0} ) $, where $ z _ {0} = f( x _ {0} , y _ {0} ) $( cf. Fig. d).
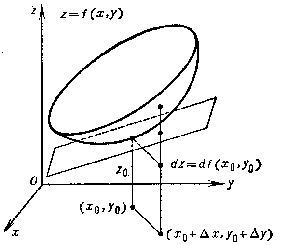
Figure: d031850d
Total differentials of higher orders are, as in the case of functions of one variable, introduced by induction, by the equation
$$ d ^ {n} z = d ( d ^ {n-} 1 z ) , $$
on the assumption that the differential $ d ^ {n-} 1 z $ is defined in some neighbourhood of the point under consideration, and that equal increments of the arguments $ dx $, $ dy $ are taken at all steps. Repeated differentials are defined in a similar manner.
Derivatives and differentials of composite functions.
Let $ w = f( u _ {1} \dots u _ {m} ) $ be a function in $ m $ variables which is differentiable at each point of an open domain $ D $ of the $ m $- dimensional Euclidean space $ \mathbf R ^ {m} $, and let $ m $ functions $ u _ {1} = \phi _ {1} ( x _ {1} \dots x _ {n} ) \dots u _ {m} = \phi _ {m} ( x _ {1} \dots x _ {n} ) $ in $ n $ variables be defined in an open domain $ G $ of the $ n $- dimensional Euclidean space $ \mathbf R ^ {n} $. Finally, let the point $ ( u _ {1} \dots u _ {m} ) $, corresponding to a point $ ( x _ {1} \dots x _ {n} ) \in G $, be contained in $ D $. The following theorems then hold:
A) If the functions $ \phi _ {1} \dots \phi _ {m} $ have finite partial derivatives with respect to $ x _ {1} \dots x _ {n} $, the composite function $ w = f( u _ {1} \dots u _ {m} ) $ in $ x _ {1} \dots x _ {n} $ also has finite partial derivatives with respect to $ x _ {1} \dots x _ {n} $, and
$$ \begin{array}{c} \frac{\partial w }{\partial x _ {1} } = \frac{\partial f }{\partial u _ {1} } \frac{\partial u _ {1} }{\partial x _ {1} } + \dots + \frac{\partial f }{\partial u _ {n} } \frac{\partial u _ {n} }{\partial x _ {1} } , \\ {} \dots \dots \dots \dots \dots \dots \\ \frac{\partial w }{\partial x _ {n} } = \frac{\partial f }{\partial u _ {1} } \frac{\partial u _ {1} }{\partial x _ {n} } + \dots + \frac{\partial f }{\partial u _ {n} } \frac{\partial u _ {n} }{\partial x _ {n} } . \end{array} $$
B) If the functions $ \phi _ {1} \dots \phi _ {m} $ are differentiable with respect to all variables at a point $ ( x _ {1} \dots x _ {n} ) \in G $, then the composite function $ w = f ( u _ {1} \dots u _ {m} ) $ is also differentiable at that point, and
$$ dw = \frac{\partial f }{\partial u _ {1} } du _ {1} + \dots + \frac{\partial f }{\partial u _ {n} } du _ {n} , $$
where $ du _ {1} \dots du _ {m} $ are the differentials of the functions $ u _ {1} \dots u _ {m} $. Thus, the property of invariance of the first differential also applies to functions in several variables. It does not usually apply to differentials of the second or higher orders.
Differential calculus is also employed in the study of the properties of functions in several variables: finding extrema, the study of functions defined by one or more implicit equations, the theory of surfaces, etc. One of the principal tools for such purposes is the Taylor formula.
The concepts of derivative and differential and their simplest properties, connected with arithmetical operations over functions and superposition of functions, including the property of invariance of the first differential, are extended, practically unchanged, to complex-valued functions in one or more variables, to real-valued and complex-valued vector functions in one or several real variables, and to complex-valued functions and vector functions in one or several complex variables. In functional analysis the ideas of the derivative and the differential are extended to functions of the points in an abstract space.
For the history of differential and integral calculus, see [1]–[6]. For studies by the founders and creators of differential and integral calculus, see [7]–[13]. For handbooks and textbooks of differential and integral calculus, see [14]–[24].
References
| [1] | , The history of mathematics from Antiquity to the beginning of the XIX-th century , 1–3 , Moscow (1970–1972) (In Russian) |
| [2] | K.A. Rybnikov, "A history of mathematics" , 1–2 , Moscow (1960–1963) (In Russian) |
| [3] | H. Wieleitner, "Die Geschichte der Mathematik von Descartes bis zum Hälfte des 19. Jahrhunderts" , de Gruyter (1923) |
| [4] | D.J. Struik, "A concise history of mathematics" , 1–2 , Dover, reprint (1948) (Translated from Dutch) MR0026572 Zbl 0032.09701 |
| [5] | N. Bourbaki, "Eléments d'histoire de mathématique" , Hermann (1960) MR0113788 |
| [6] | M. Cantor, "Vorlesungen über die Geschichte der Mathematik" , 1–4 , Teubner (1900–1908) Zbl 38.0001.01 Zbl 39.0002.02 Zbl 26.0001.01 Zbl 25.0001.02 |
| [7] | I. Newton, "The mathematical papers of I. Newton" , 1–8 , Cambridge Univ. Press (1967–1981) |
| [8] | G. Leibniz, "Mathematische Schriften" , 1–7 , G. Olms (1971) MR2490564 MR2490563 MR0141581 MR0141580 MR0141579 MR0141578 MR0141577 MR0141576 MR0141575 Zbl 1202.01108 Zbl 1155.01006 Zbl 1038.01515 Zbl 0866.01008 Zbl 0728.01028 |
| [9] | G.F. l'Hospital, "Analyse des infiniment petits pour l'intellligence des lignes courbes" , Paris (1696) |
| [10] | L. Euler, "Einleitung in die Analysis des Unendlichen" , Springer (1983) (Translated from Latin) MR0715928 Zbl 0521.01031 |
| [11] | L. Euler, "Institutiones calculi differentialis" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 10 , Teubner (1980) MR2384378 |
| [12] | A.L. Cauchy, "Oeuvres II Série" , 4–5 , Gauthier-Villars (1894–1903) Zbl 44.0016.02 Zbl 39.0022.04 Zbl 34.0016.01 Zbl 19.0019.01 |
| [13] | A.L. Cauchy, "Algebraische Analyse" , Springer (1885) (Translated from French) |
| [14] | E. Goursat, "Cours d'analyse mathématique" , 1 , Gauthier-Villars (1910) MR1296666 MR1296665 MR1296664 MR1519291 |
| [15] | Ch.J. de la Valleé-Poussin, "Cours d'analyse infinitésimales" , 1 , Libraire Univ. Louvain (1923) |
| [16] | R. Courant, "Differential and integral calculus" , 1 , Blackie (1948) (Translated from German) MR1009559 MR1009558 MR0364564 MR0364563 MR1524132 MR1523353 Zbl 0635.26002 Zbl 0635.26001 Zbl 0224.26001 Zbl 0018.30001 Zbl 0011.05802 Zbl 63.0162.01 Zbl 62.1165.04 Zbl 60.0951.02 |
| [17] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) MR0385023 Zbl 0346.26002 |
| [18] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [19] | L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1973) (In Russian) MR1617334 MR1070567 MR1070566 MR1070565 MR0866891 MR0767983 MR0767982 MR0628614 MR0619214 Zbl 1080.00002 Zbl 1080.00001 Zbl 1060.26002 Zbl 0869.00003 Zbl 0696.26002 Zbl 0703.26001 Zbl 0609.00001 Zbl 0632.26001 Zbl 0485.26002 Zbl 0485.26001 |
| [20] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) Zbl 0397.00003 Zbl 0384.00004 |
| [21] | G.P. Tolstov, "Elements of mathematical analysis" , 1–2 , Moscow (1974) (In Russian) MR0357695 MR0354961 |
| [22] | V.I. Smirnov, "A course of higher mathematics" , 2 , Addison-Wesley (1964) (Translated from Russian) MR0182690 MR0182688 MR0182687 MR0177069 MR0168707 Zbl 0122.29703 Zbl 0121.25904 Zbl 0118.28402 Zbl 0117.03404 |
| [23] | G.M. Fichtenholz, "Differential und Integralrechnung" , 1 , Deutsch. Verlag Wissenschaft. (1964) MR1191905 MR1056870 MR1056869 MR0887101 MR0845556 MR0845555 MR0524565 MR0473117 MR0344040 MR0344039 MR0238635 MR0238637 MR0238636 Zbl 0143.27002 |
| [24] | A. Ya. Khinchin, "Eight lectures on mathematical analysis" , Moscow-Leningrad (1948) (In Russian) Zbl 0131.05005 |
Comments
See also Gâteaux derivative; Fréchet derivative; Schwarz differential for generalizations. There are many books treating the subject mentioned above. A few are given below.
References
| [a1] | T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1964) MR1908007 MR1182316 MR1182315 MR0595410 MR1536963 MR1535772 MR0271732 MR0248290 MR0247001 MR0261376 MR0250092 MR0236734 MR0236733 MR0214705 MR1532185 MR1531712 MR0087718 Zbl 0123.25902 |
| [a2] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) MR0344384 Zbl 0309.26002 |
| [a3] | C.F. Boyer, "A history of mathematics" , Wiley (1968) MR0234791 Zbl 0182.30401 |
| [a4] | B.D. Craven, "Functions of several variables" , Chapman & Hall (1981) MR0636505 Zbl 0485.26004 |
| [a5] | M. Spivak, "Calculus on manifolds" , Benjamin/Cummings (1965) MR0209411 Zbl 0141.05403 |
| [a6] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1960) (Translated from French) MR0120319 Zbl 0100.04201 |
Differential calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_calculus&oldid=53430