Curvature
A collective term for a series of quantitative characteristics (in terms of numbers, vectors, tensors) describing the degree to which some object (a curve, a surface, a Riemannian space, etc.) deviates in its properties from certain other objects (a straight line, a plane, a Euclidean space, etc.) which are considered to be flat. The concepts of curvature are usually defined locally, i.e. at each point. These concepts of curvature are connected with the examination of deviations which are small to the second order; hence the object in question is assumed to be specified by 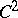 -smooth functions. In some cases the concepts are defined in terms of integrals, and they remain valid without the
-smooth functions. In some cases the concepts are defined in terms of integrals, and they remain valid without the 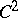 -smoothness condition. As a rule, if the curvature vanishes at all points, the object in question is identical (in small sections, not in the large) with the corresponding "flat" object.
-smoothness condition. As a rule, if the curvature vanishes at all points, the object in question is identical (in small sections, not in the large) with the corresponding "flat" object.
The curvature of a curve.
Let 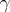 be a regular curve in the
be a regular curve in the  -dimensional Euclidean space, parametrized in terms of its natural parameter
-dimensional Euclidean space, parametrized in terms of its natural parameter 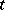 . Let
. Let  and
and 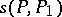 be the angle between the tangents to
be the angle between the tangents to 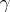 at the points
at the points 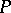 and
and 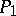 of
of 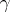 and the length of the arc of the curve between
and the length of the arc of the curve between 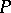 and
and 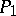 , respectively. Then the limit
, respectively. Then the limit
 |
is called the curvature of the curve 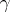 at
at 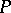 . The curvature of the curve is equal to the absolute value of the vector
. The curvature of the curve is equal to the absolute value of the vector  , and the direction of this vector is just the direction of the principal normal to the curve. For the curve
, and the direction of this vector is just the direction of the principal normal to the curve. For the curve 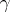 to coincide with some segment of a straight line or with an entire line it is necessary and sufficient that its curvature
to coincide with some segment of a straight line or with an entire line it is necessary and sufficient that its curvature 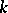 vanishes identically.
vanishes identically.
The curvature of a surface.
Let 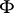 be a regular surface in the three-dimensional Euclidean space. Let
be a regular surface in the three-dimensional Euclidean space. Let 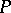 be a point of
be a point of 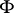 ,
, 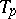 the tangent plane to
the tangent plane to 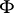 at
at 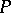 ,
, 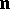 the normal to
the normal to 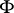 at
at  , and
, and 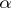 the plane through
the plane through 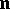 and some unit vector
and some unit vector  in
in 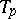 . The intersection
. The intersection  of the plane
of the plane  and the surface
and the surface 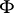 is a curve, called the normal section of the surface
is a curve, called the normal section of the surface 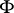 at the point
at the point 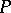 in the direction
in the direction  . The number
. The number
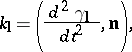 |
where 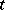 is the natural parameter on
is the natural parameter on 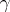 , is called the normal curvature of
, is called the normal curvature of 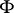 in the direction
in the direction  . The normal curvature is equal to the curvature of the curve
. The normal curvature is equal to the curvature of the curve 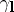 up to the sign.
up to the sign.
The tangent plane 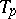 contains two perpendicular directions
contains two perpendicular directions 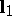 and
and  such that the normal curvature in any direction can be expressed by Euler's formula:
such that the normal curvature in any direction can be expressed by Euler's formula:
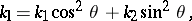 |
where 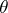 is the angle between
is the angle between  and
and  . The numbers
. The numbers 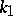 and
and 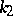 are called the principal curvatures, and the directions
are called the principal curvatures, and the directions 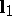 and
and 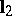 are known as the principal directions of the surface. The principal curvatures are extremal values of the normal curvature. The construction of the normal curvature at a given point of the surface may be represented graphically as follows. When
are known as the principal directions of the surface. The principal curvatures are extremal values of the normal curvature. The construction of the normal curvature at a given point of the surface may be represented graphically as follows. When 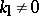 , the equation
, the equation
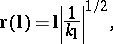 |
where 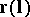 is the radius vector, defines a certain curve of the second order in the tangent plane
is the radius vector, defines a certain curve of the second order in the tangent plane 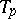 , known as the Dupin indicatrix. The Dupin indicatrix can only be one of the following three curves: an ellipse, a hyperbola or a pair of parallel lines. The points of the surface are accordingly classified as elliptic, hyperbolic or parabolic. At an elliptic point, the second fundamental form of the surface is of fixed sign; at a hyperbolic point the form is of variable sign; and at a parabolic point it is degenerate. If all normal curvatures at a point are zero, the point is said to be flat. If the Dupin indicatrix is a circle it is called an umbilical (or spherical) point.
, known as the Dupin indicatrix. The Dupin indicatrix can only be one of the following three curves: an ellipse, a hyperbola or a pair of parallel lines. The points of the surface are accordingly classified as elliptic, hyperbolic or parabolic. At an elliptic point, the second fundamental form of the surface is of fixed sign; at a hyperbolic point the form is of variable sign; and at a parabolic point it is degenerate. If all normal curvatures at a point are zero, the point is said to be flat. If the Dupin indicatrix is a circle it is called an umbilical (or spherical) point.
The principal directions are uniquely determined (up to the order), unless the point in question is an umbilical point or a flat point. In these cases every direction is principal. In this connection one has the following theorem of Rodrigues: A direction  is principal if and only if
is principal if and only if
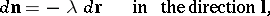 |
where  is the radius vector of the surface and
is the radius vector of the surface and 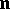 the unit normal vector.
the unit normal vector.
A curve on a surface is called a curvature line if its direction at every point is principal. In a neighbourhood of every point 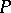 on a surface, other than an umbilical point or a flat point, the surface may be so parametrized that its coordinate curves are curvature lines.
on a surface, other than an umbilical point or a flat point, the surface may be so parametrized that its coordinate curves are curvature lines.
The quantity
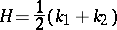 |
is called the mean curvature of the surface. The quantity
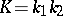 |
is called the Gaussian (or total) curvature of the surface. The Gaussian curvature is an object of the intrinsic geometry of the surface, i.e. it can be expressed in terms of the first fundamental form:
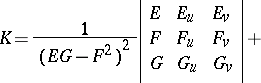 | (1) |
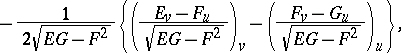 |
where 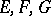 are the coefficients of the first fundamental form of the surface.
are the coefficients of the first fundamental form of the surface.
Using formula (1), one defines the Gaussian curvature for an abstract two-dimensional Riemannian manifold with line element 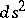 . A surface is locally isometric to a plane if and only if its Gaussian curvature vanishes identically.
. A surface is locally isometric to a plane if and only if its Gaussian curvature vanishes identically.
The curvature of a Riemannian space.
Let 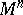 be a regular
be a regular  -dimensional Riemannian space and let
-dimensional Riemannian space and let 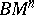 be the space of regular vector fields on
be the space of regular vector fields on 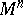 . The curvature of
. The curvature of 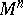 is usually characterized by the Riemann (curvature) tensor (cf. Riemann tensor), i.e. by the multilinear mapping
is usually characterized by the Riemann (curvature) tensor (cf. Riemann tensor), i.e. by the multilinear mapping
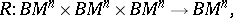 |
defined by
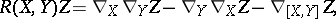 | (2) |
where  is the Levi-Civita connection on
is the Levi-Civita connection on 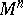 and
and 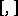 denotes the Lie bracket. If one puts
denotes the Lie bracket. If one puts 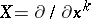 ,
, 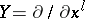 in some local coordinate system
in some local coordinate system 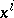 , one can rewrite (2) as follows:
, one can rewrite (2) as follows:
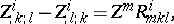 |
where; is the symbol for covariant differentiation.
Thus, the Riemann tensor is a quantitative characteristic of the non-commutativity of the second covariant derivatives in a Riemannian space. It also yields a quantitative description of certain other properties of Riemannian spaces — properties that distinguish them from Euclidean spaces.
The coefficients of the Riemann tensor in the local coordinate system 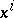 may be expressed in terms of the Christoffel symbols and the coefficients of the metric tensor, as follows:
may be expressed in terms of the Christoffel symbols and the coefficients of the metric tensor, as follows:
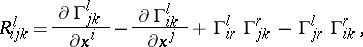 |
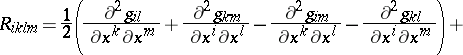 |
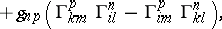 |
where 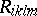 is the Riemann tensor with fourth covariant index, or — in a coordinate-free notation — the mapping
is the Riemann tensor with fourth covariant index, or — in a coordinate-free notation — the mapping 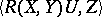 (where
(where 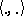 denotes the scalar product).
denotes the scalar product).
The Riemann tensor possesses the following symmetry properties:
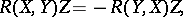 |
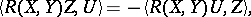 |
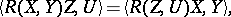 |
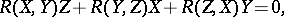 |
which may be written in local coordinates in the form:
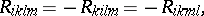 |
 |
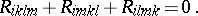 |
The Riemann tensor has 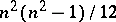 algebraically independent components. The covariant derivatives of the Riemann tensor satisfy the (second) Bianchi identity:
algebraically independent components. The covariant derivatives of the Riemann tensor satisfy the (second) Bianchi identity:
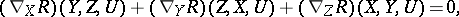 |
where 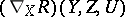 is the covariant derivative of
is the covariant derivative of 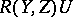 with respect to
with respect to 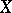 . In local coordinates, this identity is
. In local coordinates, this identity is
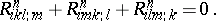 |
The Riemann tensor is sometimes defined with the opposite sign.
A Riemannian space is locally isometric to a Euclidean space if and only if its Riemann tensor vanishes identically.
Another, equivalent, approach is sometimes adopted with regard to describing the curvature of a Riemannian space 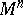 . Let
. Let 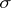 be a two-dimensional linear space in the tangent space
be a two-dimensional linear space in the tangent space 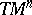 to
to 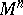 at a point
at a point 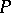 . Then the sectional curvature of
. Then the sectional curvature of 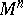 at
at 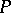 in the direction
in the direction 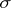 is defined as
is defined as
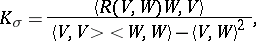 |
where  and
and 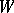 are vectors defining
are vectors defining 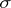 . The same area element
. The same area element 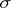 may be defined by different vectors
may be defined by different vectors 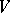 and
and  , but
, but 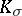 is independent of the specific vectors chosen. For a two-dimensional Riemannian space, the sectional curvature coincides with the Gaussian curvature. The Riemann tensor can be expressed in terms of the sectional curvatures:
is independent of the specific vectors chosen. For a two-dimensional Riemannian space, the sectional curvature coincides with the Gaussian curvature. The Riemann tensor can be expressed in terms of the sectional curvatures:
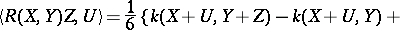 |
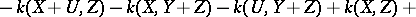 |
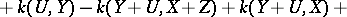 |
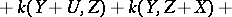 |
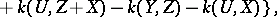 |
where
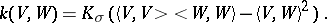 |
Weaker characteristics of the curvature of a Riemannian space are also used — the Ricci tensor, or Ricci curvature:
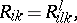 |
and the scalar curvature:
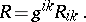 |
The Ricci tensor is symmetric: 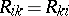 .
.
The curvature is sometimes characterized in terms of more complicated constructions — particularly quadratic ones — based on the Riemann tensor. One of the most common invariants of this type is
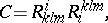 |
which is used in investigating the Schwarzschild gravity field.
For a two-dimensional space, the Riemann tensor is
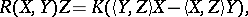 | (3) |
where 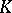 is the Gaussian curvature. In this case the scalar curvature is equal to
is the Gaussian curvature. In this case the scalar curvature is equal to 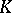 . For a three-dimensional space the Riemann tensor has the form
. For a three-dimensional space the Riemann tensor has the form
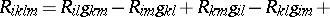 |
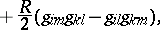 |
where 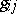 is the metric tensor,
is the metric tensor, 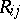 is the Ricci tensor and
is the Ricci tensor and 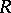 is the scalar curvature.
is the scalar curvature.
If the sectional curvatures are independent both of the point and of the two-dimensional direction, the space 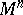 is known as a space of constant curvature; the Riemann tensor of such a space has the form (3) (the constant
is known as a space of constant curvature; the Riemann tensor of such a space has the form (3) (the constant 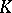 is then called the curvature of the space
is then called the curvature of the space 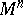 ). When
). When 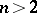 it turns out that, if in all points the curvature is independent of the direction, then
it turns out that, if in all points the curvature is independent of the direction, then 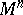 is a space of constant curvature (Schur's theorem).
is a space of constant curvature (Schur's theorem).
The curvature of submanifolds.
Let 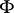 be a regular surface in
be a regular surface in 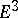 , let
, let 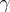 be a curve on
be a curve on 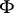 and let
and let 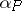 be the tangent plane to
be the tangent plane to 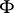 at a point
at a point 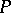 on
on 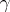 . Suppose that a small neighbourhood of
. Suppose that a small neighbourhood of 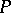 is projected onto the plane
is projected onto the plane 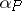 and let
and let 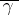 be the projection of the curve
be the projection of the curve  on
on 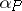 . The geodesic curvature
. The geodesic curvature 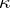 of the curve
of the curve 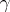 at
at 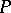 is defined as the number equal in absolute value to the curvature of the curve
is defined as the number equal in absolute value to the curvature of the curve 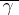 at
at 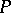 . The geodesic curvature is considered positive if the rotation of the tangent to
. The geodesic curvature is considered positive if the rotation of the tangent to 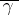 as one passes through
as one passes through 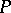 forms a right-handed screw with the direction of the normal to the surface. The geodesic curvature is an object of the intrinsic geometry of
forms a right-handed screw with the direction of the normal to the surface. The geodesic curvature is an object of the intrinsic geometry of 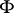 . It can be evaluated from the formula
. It can be evaluated from the formula
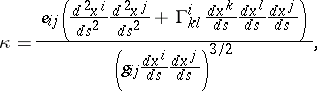 | (4) |
where 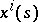 is the natural equation of the curve
is the natural equation of the curve 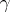 in local coordinates
in local coordinates 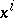 on
on 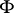 ,
, 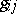 are the components of the metric tensor of
are the components of the metric tensor of 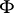 in these coordinates,
in these coordinates, 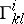 are the Christoffel symbols, and
are the Christoffel symbols, and 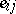 is the totally discriminant tensor. Using formula (4) one can define the geodesic curvature for curves on an abstract two-dimensional Riemannian space. A curve on a Riemannian manifold coincides with a geodesic or with part of a geodesic if and only if its geodesic curvature vanishes identically.
is the totally discriminant tensor. Using formula (4) one can define the geodesic curvature for curves on an abstract two-dimensional Riemannian space. A curve on a Riemannian manifold coincides with a geodesic or with part of a geodesic if and only if its geodesic curvature vanishes identically.
Let 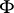 be a two-dimensional submanifold of a three-dimensional Riemannian space
be a two-dimensional submanifold of a three-dimensional Riemannian space 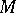 . There are two approaches to the definition of the curvature for
. There are two approaches to the definition of the curvature for 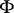 . On the one hand, one can consider
. On the one hand, one can consider 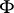 as a Riemannian space whose metric is induced by that of
as a Riemannian space whose metric is induced by that of 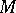 , and then use formula (1) to define its curvature. This yields what is called the internal curvature. On the other hand, one can carry out the same construction that gives the definition of the curvature for surfaces in a Euclidean space and apply it to submanifolds in a Riemannian space. The result is a different concept of the curvature, known as the external curvature. One has the following relationship:
, and then use formula (1) to define its curvature. This yields what is called the internal curvature. On the other hand, one can carry out the same construction that gives the definition of the curvature for surfaces in a Euclidean space and apply it to submanifolds in a Riemannian space. The result is a different concept of the curvature, known as the external curvature. One has the following relationship:
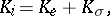 |
where 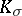 is the curvature of
is the curvature of 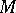 in the direction of the tangent plane to
in the direction of the tangent plane to  , and
, and 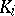 and
and 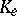 are the internal and external curvatures, respectively.
are the internal and external curvatures, respectively.
The concepts of normal, internal and external curvatures can be generalized with respect to the dimension and codimension of the submanifold in question.
The concept of the Riemann tensor may be generalized to various spaces with a weaker structure than Riemannian spaces. For example, the Riemann and Ricci tensors depend only on the affine structure of the space and may also be defined in spaces with an affine connection, although in that case they do not possess all the symmetry properties as above. For example, 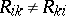 . Other examples of this type are the conformal curvature tensor and the projective curvature tensor. The conformal curvature tensor (Weyl tensor) is
. Other examples of this type are the conformal curvature tensor and the projective curvature tensor. The conformal curvature tensor (Weyl tensor) is
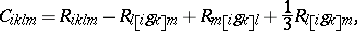 |
where the brackets denote alternation with respect to the relevant indices. Vanishing of the conformal curvature tensor is a necessary and sufficient condition for the space to coincide locally with a conformal Euclidean space. The projective curvature tensor is
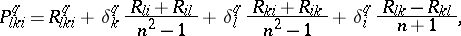 |
where 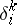 is the Kronecker symbol and
is the Kronecker symbol and  is the dimension of the space. Vanishing of the projective curvature tensor is a necessary and sufficient condition for the space to coincide locally with a projective Euclidean space.
is the dimension of the space. Vanishing of the projective curvature tensor is a necessary and sufficient condition for the space to coincide locally with a projective Euclidean space.
The concept of curvature generalizes to the case of non-regular objects, in particular, to the case of the theory of two-dimensional manifolds of bounded curvature. Here the curvature in a space is defined not at a point, but in a domain, and one is concerned with the total or integral curvature of a domain. In the regular case the total curvature is equal to the integral of the Gaussian curvature. The total curvature of a geodesic triangle may be expressed in terms of the angles 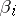 at its vertices:
at its vertices:
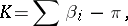 | (5) |
this relationship is a special case of the Gauss–Bonnet theorem. Formula (5) has been used as a basis for the definition of the total curvature in manifolds of bounded curvature.
The curvature is one of the fundamental concepts in modern differential geometry. Restrictions on the curvature usually yield meaningful information about an object. For example, in the theory of surfaces in  , the sign of the Gaussian curvature defines the type of a point (elliptic, hyperbolic or parabolic). Surfaces with an everywhere non-negative Gaussian curvature share a whole spectrum of properties, by virtue of which they can be grouped together in one natural class (see [4], [6]). Surfaces with zero mean curvature (see Minimal surface) have many specific properties. The theory of non-regular surfaces especially studies classes of surfaces of bounded integral absolute Gaussian or mean curvature.
, the sign of the Gaussian curvature defines the type of a point (elliptic, hyperbolic or parabolic). Surfaces with an everywhere non-negative Gaussian curvature share a whole spectrum of properties, by virtue of which they can be grouped together in one natural class (see [4], [6]). Surfaces with zero mean curvature (see Minimal surface) have many specific properties. The theory of non-regular surfaces especially studies classes of surfaces of bounded integral absolute Gaussian or mean curvature.
In Riemannian spaces, a uniform bound on the sectional curvatures 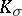 at any point and in any two-dimensional direction makes it possible to use comparison theorems. The latter enable one to compare the rate of deviation of the geodesics and the volumes of domains in a given space with the characteristics of the corresponding curves and domains in a space of constant curvature. Some of the restrictions on
at any point and in any two-dimensional direction makes it possible to use comparison theorems. The latter enable one to compare the rate of deviation of the geodesics and the volumes of domains in a given space with the characteristics of the corresponding curves and domains in a space of constant curvature. Some of the restrictions on 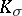 even predetermine the topological structure of the space as a whole. For example:
even predetermine the topological structure of the space as a whole. For example:
The sphere theorem. Let 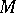 be a complete simply-connected Riemannian space of dimension
be a complete simply-connected Riemannian space of dimension 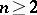 and let
and let 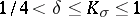 . Then
. Then 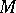 is homeomorphic to the sphere
is homeomorphic to the sphere 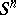 .
.
The Hadamard–Cartan and Gromoll–Meyer theorems. Let 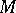 be a complete Riemannian space of dimension
be a complete Riemannian space of dimension 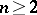 . If
. If 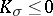 everywhere and
everywhere and 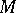 is simply connected, or if
is simply connected, or if 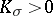 everywhere and
everywhere and 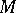 is not compact, then
is not compact, then 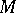 is homeomorphic to the Euclidean space
is homeomorphic to the Euclidean space 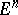 .
.
The concepts of curvature are utilized in various natural sciences. Thus, when a body is moving along a trajectory, there is a relationship between the curvature of the trajectory and the centrifugal force. The Gaussian curvature first appeared in Gauss' work on cartography. The mean curvature of the surface of a liquid is related to the capillary effect. In relativity theory there is a connection between the distribution of mass and energy (more precisely, between the energy-momentum tensor) and the curvature of space-time. The conformal curvature tensor is used in the theory of formation of particles in a gravitational field.
References
| [1] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [2] | A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian) |
| [3] | W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Elementare Differentialgeometrie" , 1 , Springer (1921) |
| [4] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
| [5] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [6] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
Formula (1) can be expressed in various ways, e.g., in [2] it reads:
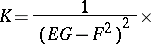 |
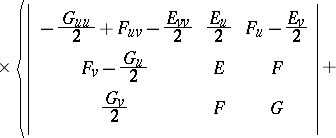 |
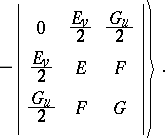 |
The first Bianchi identity is the usual name given to the fourth symmetry relation for the Riemann tensor, i.e. to 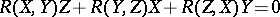 . The second Bianchi identity is the relation
. The second Bianchi identity is the relation
 |
called the Bianchi identity above.
Such concepts as mean curvature, conformal curvature tensors, geodesic curvature, and projective curvature tensor are also defined in higher dimensional settings (than surfaces), cf. e.g. [a2] (mean curvature), [a3], [1] (conformal and projective curvature tensors). (Cf. also Conformal Euclidean space.) The absolute value of the geodesic curvature of a curve on a surface is 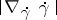 , where
, where 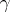 is assumed to be described by its arc length parameter (natural parameter) and
is assumed to be described by its arc length parameter (natural parameter) and  is the Levi-Civita connection on the surface. For the concepts of natural parameter and natural equation of a curve, cf. Natural equation. The various fundamental (quadratic) forms of a surface are discussed in Fundamental forms of a surface; Geometry of immersed manifolds and Second fundamental form.
is the Levi-Civita connection on the surface. For the concepts of natural parameter and natural equation of a curve, cf. Natural equation. The various fundamental (quadratic) forms of a surface are discussed in Fundamental forms of a surface; Geometry of immersed manifolds and Second fundamental form.
The sectional curvature of a Riemannian space 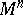 at
at 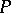 in the direction of the tangent plane
in the direction of the tangent plane 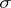 is also called the Riemannian curvature.
is also called the Riemannian curvature.
Let  denote the Ricci tensor and let
denote the Ricci tensor and let 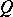 be the quadratic form on
be the quadratic form on 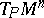 given by
given by 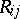 at
at 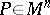 . Then the value
. Then the value 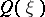 for a unit vector
for a unit vector 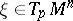 is the mean of
is the mean of 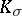 for all plane directions
for all plane directions 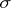 in
in 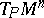 containing
containing 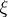 , and is called the Ricci curvature or mean curvature of the direction
, and is called the Ricci curvature or mean curvature of the direction  at
at 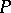 . The mean
. The mean 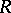 of all the
of all the 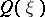 is the scalar curvature at
is the scalar curvature at 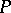 , cf. also Ricci tensor and Ricci curvature. If
, cf. also Ricci tensor and Ricci curvature. If 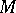 is a Kähler manifold and
is a Kähler manifold and 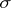 is restricted to a complex plane (i.e. a plane invariant under the almost-complex structure), then
is restricted to a complex plane (i.e. a plane invariant under the almost-complex structure), then 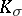 is called the holomorphic sectional curvature.
is called the holomorphic sectional curvature.
For a simply-closed space curve 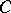 of length
of length 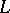 the integral
the integral 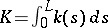 is called the total curvature of
is called the total curvature of 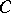 ; generally
; generally 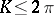 , and
, and 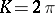 if and only if
if and only if 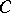 is a closed curve lying in a plane (W. Fenchel). Fix an origin 0 in
is a closed curve lying in a plane (W. Fenchel). Fix an origin 0 in 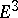 and consider the unit sphere
and consider the unit sphere 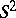 around 0. For each point
around 0. For each point  of
of 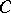 let
let 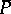 be the point on
be the point on 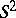 such that
such that 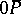 is the (displaced) unit tangent vector to
is the (displaced) unit tangent vector to 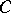 at
at  . As
. As 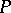 runs over
runs over  the
the 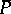 trace out a curve on
trace out a curve on  , the spherical indicatrix
, the spherical indicatrix 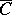 of
of 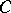 . The correspondence
. The correspondence 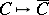 is called the spherical representation. The total curvature of
is called the spherical representation. The total curvature of 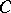 is equal to the length of
is equal to the length of 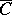 . Instead of the tangents to
. Instead of the tangents to 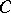 one can also use the principal normal and binormal vectors and perform a similar construction yielding other spherical indicatrices, cf. Spherical indicatrix.
one can also use the principal normal and binormal vectors and perform a similar construction yielding other spherical indicatrices, cf. Spherical indicatrix.
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
| [a2] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) pp. 33 |
| [a3] | J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) pp. Chapt. VI (Translated from German) |
Curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Curvature&oldid=12026