Cobordism
cobordism theory
A generalized cohomology theory determined by spectra of Thom spaces and related to various structures in the stable tangent or normal bundle to a manifold. Cobordism theory is dual (in the sense of  -duality) to the theory of bordism.
-duality) to the theory of bordism.
The simplest example of cobordism is orthogonal or non-oriented cobordism. Let 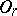 by the group of orthogonal transformations of the Euclidean space
by the group of orthogonal transformations of the Euclidean space 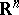 , and
, and 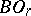 its classifying space. The standard imbedding
its classifying space. The standard imbedding 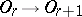 defines a mapping
defines a mapping 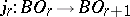 taking the universal fibre bundle
taking the universal fibre bundle  over
over  into the bundle
into the bundle 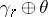 , where
, where 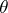 is the one-dimensional trivial bundle over
is the one-dimensional trivial bundle over  . If
. If 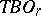 is the Thom space of
is the Thom space of 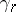 , then one obtains a mapping
, then one obtains a mapping 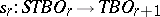 induced by
induced by  , where
, where 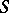 is suspension. The sequence
is suspension. The sequence 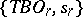 forms a spectrum of spaces and therefore defines a cohomology theory, called the theory of orthogonal cobordism or non-oriented cobordism or
forms a spectrum of spaces and therefore defines a cohomology theory, called the theory of orthogonal cobordism or non-oriented cobordism or 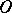 -cobordism; it is denoted by
-cobordism; it is denoted by 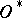 . The group
. The group 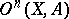 of
of  -dimensional
-dimensional 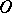 -cobordism of the pair
-cobordism of the pair 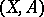 is defined as
is defined as
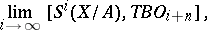 |
where 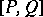 is the set of homotopy classes of mappings from
is the set of homotopy classes of mappings from  into
into 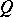 . Here
. Here 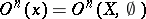 ,
, 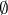 is the empty set, and by
is the empty set, and by  one means the disjoint union of
one means the disjoint union of  and a point. The group
and a point. The group  , where
, where 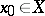 , is called the reduced group of
, is called the reduced group of  -dimensional
-dimensional 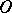 -cobordism
-cobordism 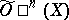 of
of  . The generalized homology theory dual to the
. The generalized homology theory dual to the 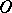 -cobordism theory is called
-cobordism theory is called 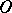 -bordism theory. The groups
-bordism theory. The groups 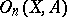 of
of  -dimensional bordism of the pair
-dimensional bordism of the pair 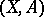 are defined as
are defined as
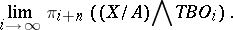 |
The groups of  -dimensional
-dimensional 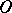 -bordism of a point are denoted by
-bordism of a point are denoted by 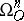 and the
and the  -dimensional
-dimensional 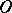 -bordism of a point by
-bordism of a point by 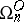 ; the latter can be described purely geometrically. Furthermore,
; the latter can be described purely geometrically. Furthermore, 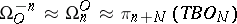 ,
, 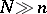 , so that it can be interpreted both as a cobordism group and a bordism group (see bordism, where it is denoted by
, so that it can be interpreted both as a cobordism group and a bordism group (see bordism, where it is denoted by 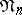 ). The total coefficient group of
). The total coefficient group of 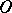 -cobordism theory, the graded group
-cobordism theory, the graded group 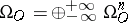 , is a ring: multiplication is induced by the Cartesian product of manifolds. Furthermore, for any finite
, is a ring: multiplication is induced by the Cartesian product of manifolds. Furthermore, for any finite 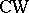 -complex
-complex 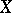 the group
the group 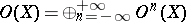 is a natural ring with respect to
is a natural ring with respect to  since the mapping
since the mapping 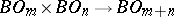 induced by the imbedding
induced by the imbedding 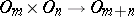 defines a mapping
defines a mapping 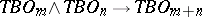 , so that
, so that 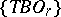 is a multiplicative spectrum of spaces.
is a multiplicative spectrum of spaces.
The general situation is described as follows. By a structural series 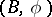 one means a sequence of bundles
one means a sequence of bundles  and mappings
and mappings 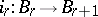 such that
such that 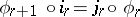 . The mapping
. The mapping 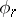 defines a vector bundle
defines a vector bundle 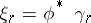 over
over 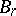 , where
, where  . Let
. Let 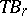 be the Thom space of the bundle
be the Thom space of the bundle 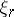 ; the above equality defines a mapping
; the above equality defines a mapping 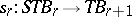 such that the sequence
such that the sequence 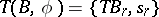 is a spectrum of spaces, hence defines a cohomology theory. It is called
is a spectrum of spaces, hence defines a cohomology theory. It is called  -cobordism theory and is denoted by
-cobordism theory and is denoted by  . Thus,
. Thus,
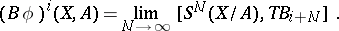 |
The coefficient group of the 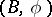 -cobordism theory is denoted by
-cobordism theory is denoted by 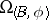 . Here,
. Here, 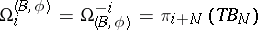 ,
, 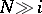 , where
, where 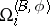 is the coefficient group of the dual
is the coefficient group of the dual  -bordism theory, which admits of a geometric definition using the concept of a so-called
-bordism theory, which admits of a geometric definition using the concept of a so-called  -structure:
-structure: 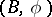 -bordancy is defined and the elements of
-bordancy is defined and the elements of 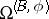 are interpreted as classes of
are interpreted as classes of 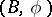 -bordant manifolds.
-bordant manifolds.
The first examples of cobordism theory arose from series of linear groups. For example, the series of orthogonal groups 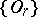 defines the structural series
defines the structural series  , where
, where 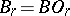 ,
, 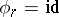 . The series
. The series 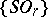 defines the structural series
defines the structural series 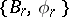 , where
, where 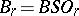 and
and 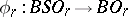 is the universal two-sheeted covering corresponding to the inclusion
is the universal two-sheeted covering corresponding to the inclusion 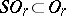 . The corresponding cobordism theory is called the theory of oriented cobordism; it is denoted by
. The corresponding cobordism theory is called the theory of oriented cobordism; it is denoted by 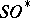 . The series of unitary groups
. The series of unitary groups 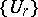 defines a theory of unitary or complex cobordism, quasi-complex cobordism, almost-complex cobordism; it is denoted by
defines a theory of unitary or complex cobordism, quasi-complex cobordism, almost-complex cobordism; it is denoted by  . Here the series
. Here the series 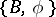 is constructed in the following way:
is constructed in the following way: 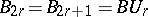 is classifying space of
is classifying space of 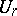 and the
and the 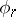 ,
, 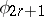 are the mappings of the classifying spaces
are the mappings of the classifying spaces 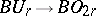 and
and 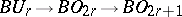 , respectively, induced by the natural imbeddings
, respectively, induced by the natural imbeddings 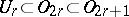 . The series of symplectic groups
. The series of symplectic groups 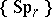 defines a theory of symplectic cobordism,
defines a theory of symplectic cobordism, 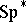 , where
, where 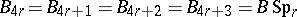 , and the
, and the 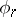 are constructed in the same way as for the unitary case. There are also cobordism theories corresponding to the series of groups
are constructed in the same way as for the unitary case. There are also cobordism theories corresponding to the series of groups 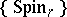 ,
, 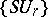 , etc. Finally, the series of identity groups
, etc. Finally, the series of identity groups 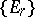 , where
, where 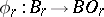 is a fibre bundle with contractible
is a fibre bundle with contractible 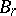 , defines a cobordism theory which is the same as the theory of stable cohomotopy groups, and therefore the dual bordism theory is isomorphic to the theory of stable homotopy groups,
, defines a cobordism theory which is the same as the theory of stable cohomotopy groups, and therefore the dual bordism theory is isomorphic to the theory of stable homotopy groups, 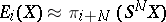 ,
, 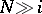 . An
. An 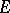 -manifold is said to be framed (trivialized) since the
-manifold is said to be framed (trivialized) since the  -structure is precisely a frame (trivialization) of the stable normal bundle.
-structure is precisely a frame (trivialization) of the stable normal bundle. 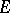 -cobordism theory is called trivialized or framed cobordism theory, its
-cobordism theory is called trivialized or framed cobordism theory, its 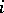 -dimensional coefficient group being denoted by
-dimensional coefficient group being denoted by  , so that
, so that 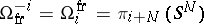 . This is the first example of a cobordism; it was due to L.S. Pontryagin, who interpreted the stable homotopy groups of the sphere as (geometrically defined) groups of framed cobordism of a point of
. This is the first example of a cobordism; it was due to L.S. Pontryagin, who interpreted the stable homotopy groups of the sphere as (geometrically defined) groups of framed cobordism of a point of 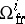 , with the aim of computing the group
, with the aim of computing the group 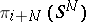 .
.
All these cobordism theories arising from series of linear groups are multiplicative, and therefore for any finite 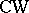 -complex
-complex 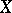 , the total (graded) cobordism group is a ring. For example, for the series of groups
, the total (graded) cobordism group is a ring. For example, for the series of groups 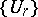 there is an imbedding
there is an imbedding 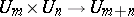 inducing a mapping
inducing a mapping
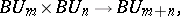 |
and therefore a mapping 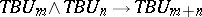 . The spectrum
. The spectrum 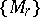 representing the theory
representing the theory 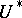 has the form
has the form 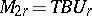 ,
, 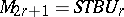 , hence there exist mappings
, hence there exist mappings 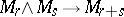 so that the spectrum of spaces
so that the spectrum of spaces 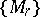 is multiplicative.
is multiplicative.
The development of cobordism theory started from the geometric definition and calculation of the groups 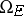 ,
, 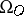 ,
, 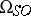 . An important role was played by Pontryagin's theorem stating that
. An important role was played by Pontryagin's theorem stating that 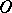 -bordant manifolds have the same Stiefel number. The study of cobordism theory was advanced by R. Thom. He introduced the spaces
-bordant manifolds have the same Stiefel number. The study of cobordism theory was advanced by R. Thom. He introduced the spaces 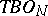 ,
, 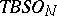 and proved the isomorphism
and proved the isomorphism  , enabling one to bring into the calculation of the cobordism rings some of the methods of homotopic topology. Thom's constructions stimulated the introduction of
, enabling one to bring into the calculation of the cobordism rings some of the methods of homotopic topology. Thom's constructions stimulated the introduction of 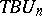 ,
, 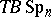 , etc., and the corresponding cobordisms. The fundamental problem of the first stage of the development of cobordism theory was the calculation of the cobordism rings of a point.
, etc., and the corresponding cobordisms. The fundamental problem of the first stage of the development of cobordism theory was the calculation of the cobordism rings of a point.
In the study of the cobordism of a point a big part is played by the characteristic classes: Chern classes for 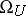 , Stiefel classes for
, Stiefel classes for 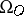 , Pontryagin and Stiefel classes for
, Pontryagin and Stiefel classes for 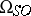 (cf. Characteristic class; Chern class; Pontryagin class). In general, given any structural series
(cf. Characteristic class; Chern class; Pontryagin class). In general, given any structural series 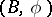 and any multiplicative cohomology theory
and any multiplicative cohomology theory 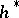 in which all bundles
in which all bundles 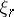 over
over 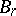 are orientable, one can define the characteristic classes as elements of the group
are orientable, one can define the characteristic classes as elements of the group 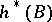 , where
, where 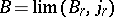 . Furthermore, the corresponding characteristic numbers, which are elements of the rings
. Furthermore, the corresponding characteristic numbers, which are elements of the rings 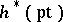 are invariant with respect to
are invariant with respect to 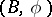 -bordancy. Let
-bordancy. Let 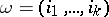 be a partition of
be a partition of  and let
and let 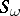 be the symmetric function of
be the symmetric function of  variables corresponding to
variables corresponding to 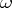 . The characteristic class
. The characteristic class 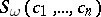 (see Chern class) is denoted by
(see Chern class) is denoted by 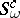 . The analogous constructions for the Pontryagin and Stiefel classes are denoted by
. The analogous constructions for the Pontryagin and Stiefel classes are denoted by 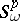 and
and 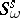 , respectively.
, respectively.
1) Unitary cobordism. The ring 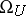 is the free graded polynomial algebra in a countable number of homogeneous generators
is the free graded polynomial algebra in a countable number of homogeneous generators
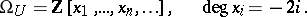 |
The set 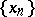 ,
, 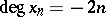 , is a system of polynomial generators if and only if
, is a system of polynomial generators if and only if
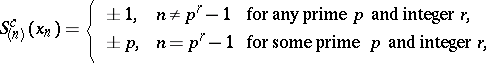 |
where 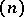 is the partition of
is the partition of  consisting of a single term. One of the systems of polynomial generators of
consisting of a single term. One of the systems of polynomial generators of 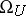 can be described as follows. Let
can be described as follows. Let 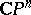 be
be  -dimensional complex projective space. The complex algebraic hypersurface of bidegree
-dimensional complex projective space. The complex algebraic hypersurface of bidegree 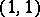 in
in 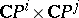 is a complex manifold. Its unitary cobordism class is denoted by
is a complex manifold. Its unitary cobordism class is denoted by 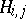 ,
, 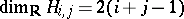 . It turns out that
. It turns out that
 |
so that an appropriate linear integer combination of elements of 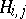 defines a generator of
defines a generator of 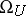 of degree
of degree 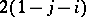 .
.
Since 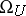 is torsion-free and
is torsion-free and 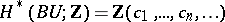 , where the
, where the 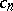 are the Chern classes,
are the Chern classes, 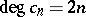 (cf. Chern class), it follows that the Chern numbers (cf. Chern number) completely determine the unitary cobordism class of an almost-complex manifold.
(cf. Chern class), it follows that the Chern numbers (cf. Chern number) completely determine the unitary cobordism class of an almost-complex manifold.
Let  be a positive integer and let
be a positive integer and let 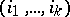 ,
, 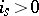 ,
, 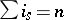 , be a partition of it. There corresponds to each
, be a partition of it. There corresponds to each 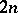 -dimensional (real dimension) almost-complex manifold
-dimensional (real dimension) almost-complex manifold 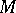 a set
a set 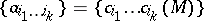 of integers, where the multi-index
of integers, where the multi-index  runs through all the partitions of
runs through all the partitions of  . A set of such integers
. A set of such integers 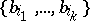 is realized as the set of Chern numbers of some almost-complex manifold in the following situation. Let
is realized as the set of Chern numbers of some almost-complex manifold in the following situation. Let 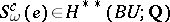 be the characteristic class given by replacing the Wu generators
be the characteristic class given by replacing the Wu generators  in the representation of
in the representation of 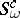 with the variables
with the variables 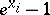 ,
, 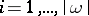 , and let
, and let 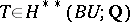 be the characteristic class given by the product of the functions
be the characteristic class given by the product of the functions 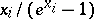 . Let
. Let 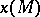 be the value of the characteristic class
be the value of the characteristic class 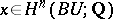 on the fundamental class
on the fundamental class 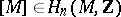 of the almost-complex manifold
of the almost-complex manifold 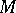 with tangent bundle
with tangent bundle 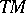 .
.
There exists for a homomorphism 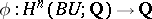 a closed almost-complex manifold
a closed almost-complex manifold 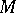 such that
such that  for all
for all  if and only if
if and only if 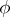 takes integer values on all the
takes integer values on all the  -dimensional components of each characteristic class
-dimensional components of each characteristic class  (Stong's theorem, see [1], Chapt. 7). Equivalently, the Hurewicz homomorphism
(Stong's theorem, see [1], Chapt. 7). Equivalently, the Hurewicz homomorphism
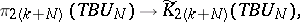 |
where 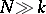 , is a monomorphism onto a direct summand (Hattori's theorem). Here
, is a monomorphism onto a direct summand (Hattori's theorem). Here 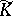 denotes reduced
denotes reduced  -theory.
-theory.
2) Non-oriented, or orthogonal, cobordism. Each element of the ring 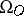 has order
has order  , and
, and
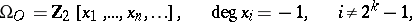 |
that is, 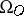 is a free polynomial
is a free polynomial 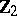 -algebra. One can choose as generator
-algebra. One can choose as generator  any element
any element 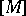 with
with 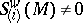 , for example,
, for example, 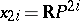 . In this theory there are analogues of the manifolds
. In this theory there are analogues of the manifolds  , obtained by replacing
, obtained by replacing 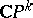 by
by 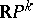 ; a suitable manifold
; a suitable manifold 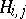 can serve as a generator of degree
can serve as a generator of degree 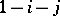 . The Stiefel numbers (cf. Stiefel number) completely define the non-orientable cobordism class of the manifold. The following theorem gives relations among the Stiefel numbers: Given a homomorphism
. The Stiefel numbers (cf. Stiefel number) completely define the non-orientable cobordism class of the manifold. The following theorem gives relations among the Stiefel numbers: Given a homomorphism 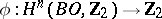 , there exists a closed
, there exists a closed  -dimensional manifold
-dimensional manifold 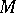 such that
such that  for all
for all 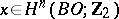 if and only if
if and only if 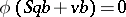 for all
for all 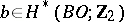 , where
, where 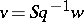 . Here
. Here 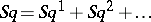 is the full Steenrod operation and
is the full Steenrod operation and 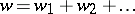 is the full Stiefel class. The ring
is the full Stiefel class. The ring 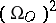 is the image of the homomorphism
is the image of the homomorphism  .
.
3) Oriented cobordism with ring  . All the elements of the torsion subgroup
. All the elements of the torsion subgroup  of this ring have order
of this ring have order  . The ring
. The ring 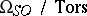 is the ring of polynomials over
is the ring of polynomials over 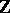 of classes
of classes 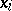 of degree
of degree 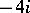 , the generators being chosen by the condition
, the generators being chosen by the condition
 |
The 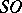 -cobordism class of a manifold is determined by the Pontryagin and Stiefel numbers (cf. Pontryagin number). The signature of the manifold is also an invariant of the cobordism class. The relations among the Stiefel numbers follow from the following fact: The image of the "forgetful" homomorphism
-cobordism class of a manifold is determined by the Pontryagin and Stiefel numbers (cf. Pontryagin number). The signature of the manifold is also an invariant of the cobordism class. The relations among the Stiefel numbers follow from the following fact: The image of the "forgetful" homomorphism 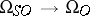 consists precisely of those cobordism classes for which all numbers containing the class
consists precisely of those cobordism classes for which all numbers containing the class 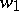 are zero. For any partition
are zero. For any partition 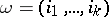 ,
,
 |
where 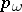 is the corresponding Pontryagin number. There do not exist any
is the corresponding Pontryagin number. There do not exist any  -prime relations among the Pontryagin numbers.
-prime relations among the Pontryagin numbers.
Similarly to the introduction of the classes 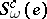 for the unitary cobordism, the classes
for the unitary cobordism, the classes 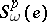 are introduced, which are symmetric functions in
are introduced, which are symmetric functions in 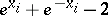 . Let
. Let 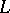 be the characteristic class defining the Hirzebruch
be the characteristic class defining the Hirzebruch  -genus. All relations among the Pontryagin numbers follow from the fact that the Pontryagin numbers are integers and
-genus. All relations among the Pontryagin numbers follow from the fact that the Pontryagin numbers are integers and 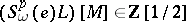 . The homomorphism
. The homomorphism 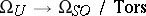 is epimorphic.
is epimorphic.
4) Special unitary cobordism with ring 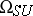 . A
. A 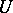 -manifold
-manifold  has an
has an  -structure if and only if
-structure if and only if 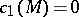 . All the elements of the torsion subgroup
. All the elements of the torsion subgroup 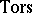 have order 2. The kernel of the homomorphism
have order 2. The kernel of the homomorphism 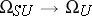 is precisely
is precisely 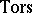 . The group
. The group 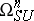 is finitely generated and
is finitely generated and 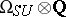 is the ring of polynomials over
is the ring of polynomials over 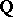 of classes
of classes  of degree
of degree  ,
,  . The torsion subgroup
. The torsion subgroup 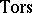 has the form
has the form 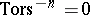 when
when 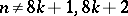 , while for
, while for 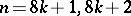 ,
, 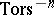 is a vector space over
is a vector space over 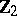 the dimension of which is the number of partitions of
the dimension of which is the number of partitions of 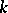 . Two
. Two 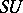 -manifolds are bordant if and only if they have the same characteristic number in integer cohomology and in
-manifolds are bordant if and only if they have the same characteristic number in integer cohomology and in 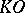 -theory.
-theory.
All relations among the Chern numbers for  -dimensional
-dimensional 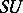 -manifolds follows from the following:
-manifolds follows from the following: 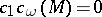 for all
for all  ;
; 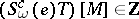 for all
for all 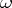 ; if
; if 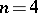
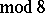 , then
, then 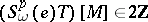 for all
for all 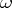 . The image of the homomorphism
. The image of the homomorphism 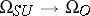 consists of the classes
consists of the classes 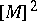 , where
, where  is an oriented manifold all Pontryagin numbers of which containing the class
is an oriented manifold all Pontryagin numbers of which containing the class 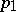 are even.
are even.
The rings  and
and 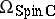 have also been completely computed. The rings
have also been completely computed. The rings 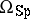 and
and 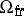 have to date (1986) not been computed. The ring
have to date (1986) not been computed. The ring 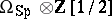 is the ring of polynomials on
is the ring of polynomials on 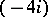 -dimensional generators. All known (1986) elements of
-dimensional generators. All known (1986) elements of 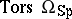 have order 2. (However there is an announcement of an element of order 4 in dimensions
have order 2. (However there is an announcement of an element of order 4 in dimensions 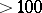 .) With regard to
.) With regard to 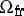 , the main result here is Serre's theorem on the finiteness of these groups. The ring
, the main result here is Serre's theorem on the finiteness of these groups. The ring 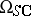 of self-adjoint cobordism has also been studied, where the objects are almost-complex manifolds with an operator given in the normal bundle which isomorphically maps the complex structure onto the adjoint. The spectrum of
of self-adjoint cobordism has also been studied, where the objects are almost-complex manifolds with an operator given in the normal bundle which isomorphically maps the complex structure onto the adjoint. The spectrum of 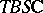 has been constructed; with regard to the groups
has been constructed; with regard to the groups 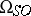 it is known that there is only
it is known that there is only  -prime torsion, but there are elements of order
-prime torsion, but there are elements of order 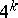 for any
for any 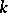 , namely
, namely 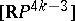 . The image
. The image 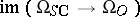 has also been calculated using the technique of formal groups (cf. Formal group).
has also been calculated using the technique of formal groups (cf. Formal group).
A mapping of one cobordism theory into another, for example,  , induces a mapping of the spectra
, induces a mapping of the spectra  . The cone of this mapping in the category of spectra gives a generalized cohomology theory. The ring of the point of the theory so obtained has the following geometric interpretation. Let
. The cone of this mapping in the category of spectra gives a generalized cohomology theory. The ring of the point of the theory so obtained has the following geometric interpretation. Let 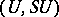 be a
be a 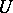 -manifold on the (possibly empty) boundary of which an
-manifold on the (possibly empty) boundary of which an 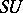 -structure is fixed. By introducing the appropriate bordism relation for
-structure is fixed. By introducing the appropriate bordism relation for  -manifolds one obtains the ring
-manifolds one obtains the ring 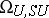 . The groups
. The groups 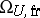 ,
,  etc., are introduced in the same way.
etc., are introduced in the same way.
So far, smooth manifolds have been considered or, equivalently, linear group representations (the structure series arising from the bundles over 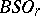 ). It is possible to consider various structures on topological manifolds, that is, to start from a group of homeomorphisms (and even proper homotopy equivalences) of
). It is possible to consider various structures on topological manifolds, that is, to start from a group of homeomorphisms (and even proper homotopy equivalences) of 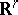 . Here the following examples are known. (Throughout, the letter
. Here the following examples are known. (Throughout, the letter  denotes passage to the oriented case.)
denotes passage to the oriented case.)
5) Piecewise-linear cobordism. The objects are piecewise-linear manifolds. The corresponding bordism relation leads to the groups 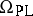 ,
, 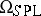 . By defining the group
. By defining the group 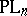 (or
(or 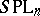 ) as the group of piecewise-linear homeomorphisms of
) as the group of piecewise-linear homeomorphisms of 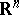 onto itself that preserve the origin (or the orientation as well), one can introduce the classifying spaces
onto itself that preserve the origin (or the orientation as well), one can introduce the classifying spaces 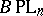 (or
(or 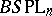 ) and the Thom spaces
) and the Thom spaces 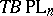 (or
(or 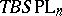 ) and construct a
) and construct a 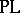 (or
(or 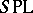 ) cobordism theory. In this connection,
) cobordism theory. In this connection,  and
and 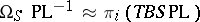 . The groups
. The groups 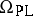 have been computed. The cobordism class of a piecewise-linear manifold is completely defined by the characteristic numbers, that is, by the elements of
have been computed. The cobordism class of a piecewise-linear manifold is completely defined by the characteristic numbers, that is, by the elements of 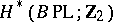 .
.
6) Topological cobordism. The objects are topological manifolds for which the groups 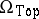 ,
, 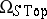 are defined. By considering the group
are defined. By considering the group  of homeomorphisms of
of homeomorphisms of 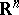 onto itself that preserve the origin, one can define the spaces
onto itself that preserve the origin, one can define the spaces 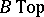 and
and 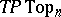 . The groups
. The groups 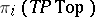 and
and 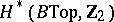 have been computed. However, the isomorphism
have been computed. However, the isomorphism 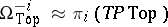 has been established for all
has been established for all 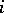 except
except 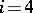 . The absence of a proof of this isomorphism is tied up with the fact that the transitivity theorem on which the isomorphism
. The absence of a proof of this isomorphism is tied up with the fact that the transitivity theorem on which the isomorphism 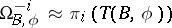 is based for topological manifolds, has not been proved in the general case (but it has not been refuted either (1986)).
is based for topological manifolds, has not been proved in the general case (but it has not been refuted either (1986)).
7) Cobordism of Poincaré complexes 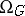 ,
, 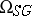 . The objects are complexes with Poincaré duality and the bordism is the corresponding equivalence relation. Such complexes have a normal spherical bundle induced from the universal bundle over
. The objects are complexes with Poincaré duality and the bordism is the corresponding equivalence relation. Such complexes have a normal spherical bundle induced from the universal bundle over 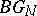 (or
(or 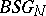 ). Here
). Here 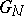 (or
(or 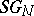 ) is an
) is an 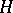 -space of homotopy equivalences (of degree 1) of the sphere
-space of homotopy equivalences (of degree 1) of the sphere 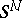 onto itself. The Thom spectra
onto itself. The Thom spectra 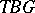 and
and 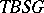 to which these give rise have finite homotopy groups, whereas the signature defines a non-trivial homomorphism
to which these give rise have finite homotopy groups, whereas the signature defines a non-trivial homomorphism 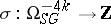 , so that, a fortiori, the mapping
, so that, a fortiori, the mapping 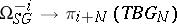 is not an isomorphism.
is not an isomorphism.
Yet another series of examples is given by cobordism of manifolds with singularities of a special type. (This is a very good technique for the construction of various cohomology theories with special properties.) One can construct along these lines a cobordism theory that is the same as ordinary singular cohomology theory and one that is the same as connected 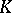 -theory.
-theory.
The second stage in the development of cobordism theory is the study of cobordisms as specific generalized cohomology theories. Let 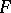 denote one of the fields
denote one of the fields 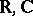 or the skew-field of quaternions
or the skew-field of quaternions  , let
, let  be the corresponding series of groups (
be the corresponding series of groups (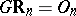 ,
, 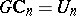 ,
, 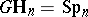 ) and let
) and let 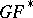 be the corresponding cobordism theory. A multiplicative generalized cohomology theory
be the corresponding cobordism theory. A multiplicative generalized cohomology theory 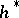 is called
is called 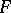 -orientable if any
-orientable if any 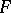 -vector bundle is
-vector bundle is 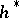 -orientable or, equivalently, if the canonical one-dimensional
-orientable or, equivalently, if the canonical one-dimensional 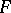 -vector bundle
-vector bundle 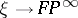 , where
, where 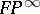 is a projective space, is
is a projective space, is 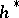 -orientable. By an
-orientable. By an 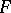 -orientation of the theory
-orientation of the theory 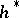 one means an
one means an  -orientation
-orientation 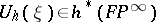 of the bundle
of the bundle 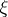 , and a theory with a chosen orientation is called oriented. The
, and a theory with a chosen orientation is called oriented. The 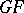 -cobordism theories have a canonical orientation because of the identification
-cobordism theories have a canonical orientation because of the identification 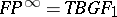 . The theory
. The theory 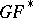 is universal in the class of
is universal in the class of 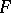 -oriented theories, that is, for any
-oriented theories, that is, for any 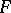 -oriented theory
-oriented theory  with
with 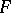 -orientation
-orientation 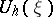 there exists a unique multiplicative homomorphism of theories
there exists a unique multiplicative homomorphism of theories 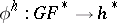 under which the canonical orientation of the theory
under which the canonical orientation of the theory 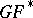 is taken to
is taken to 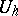 . Moreover, when
. Moreover, when 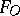 is one of the fields
is one of the fields 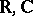 , there exist for any
, there exist for any 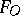 -oriented theory
-oriented theory 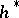 and any finite
and any finite 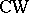 -complex
-complex 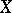 spectral sequences
spectral sequences  and
and 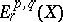 with
with
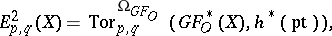 |
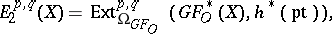 |
converging to 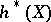 and natural in
and natural in  and
and 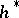 , where
, where 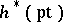 is made into an
is made into an 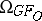 -module by means of the homomorphism
-module by means of the homomorphism 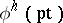 . If
. If 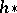 is the homology theory dual to the
is the homology theory dual to the 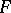 -oriented cohomology theory
-oriented cohomology theory 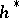 , then there is a homomorphism
, then there is a homomorphism 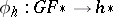 . In the case when
. In the case when 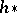 is the ordinary homology theory, it coincides with Steenrod–Thom realization of cycles (see Steenrod problem). The powerful methods of cobordism theory are connected with formal groups (cf. Formal group, [5]).
is the ordinary homology theory, it coincides with Steenrod–Thom realization of cycles (see Steenrod problem). The powerful methods of cobordism theory are connected with formal groups (cf. Formal group, [5]).
The most important and successful applications of cobordism theory are: the proof of the Atiyah–Singer index theorem for an elliptic operator and the general Riemann–Roch theorem; the study of fixed points of group actions; the classification of smooth (or piecewise-smooth) manifolds of given homotopy type; the proof of the theorem on the topological invariance of rational Pontryagin classes, and the solution of the problem of triangulability of topological manifolds.
See also the references in Bordism.
References
| [1] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [2] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) |
| [3] | S.P. Novikov, "Methods of algebraic topology from the point of view of cobordism theory" Izv. Akad. Nauk SSSR Ser. Mat. , 31 : 4 (1967) pp. 855–951 (In Russian) |
| [4] | T. Bröcker, T. Tom dieck, "Kobordismentheorie" , Springer (1970) |
| [5] | V.M. [V.M. Bukhshtaber] Buchstaber, "Cobordisms in problems of algebraic topology" J. Soviet Math. , 7 : 4 (1975) pp. 629–653 Itogi Nauk. i Tekh. Algebra. Geom. Topol. (1975) pp. 231–272 |
Comments
The letter 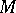 is often used to denote Thom spaces and Thom spectra. Thus, e.g.,
is often used to denote Thom spaces and Thom spectra. Thus, e.g., 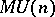 is used to denote the Thom space
is used to denote the Thom space 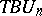 and
and  stands for the spectrum of all the
stands for the spectrum of all the 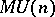 ; similarly one uses
; similarly one uses 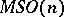 for
for  , etc. The corresponding generalized cohomology theories are then indicated by the same symbols as is customary for generalized cohomology theories defined by a spectrum; thus,
, etc. The corresponding generalized cohomology theories are then indicated by the same symbols as is customary for generalized cohomology theories defined by a spectrum; thus, 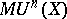 is the
is the  -th complex cobordism group of
-th complex cobordism group of 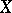 and
and 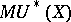 is its complex cobordism ring.
is its complex cobordism ring.
A structural series 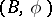 as defined above is often called a
as defined above is often called a 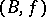 -structure (cf.
-structure (cf. 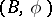 -structure, [1]).
-structure, [1]).
The general theorem that the (co)bordism group of  -dimensional
-dimensional 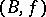 -manifolds
-manifolds 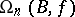 is isomorphic to
is isomorphic to 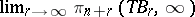 is known as the Pontryagin–Thom theorem.
is known as the Pontryagin–Thom theorem.
A complex structure on a real vector bundle 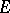 over a manifold
over a manifold  is a vector bundle morphism
is a vector bundle morphism  such that
such that 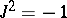 . If
. If 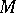 is a complex imbedded manifold without boundary
is a complex imbedded manifold without boundary 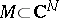 , then multiplication with
, then multiplication with  on its normal bundle defines a complex structure on that bundle (viewed as a real bundle). A weakly-complex manifold (also called a stably (almost) complex manifold) is a real manifold with a complex structure on its stable normal bundle; i.e. if
on its normal bundle defines a complex structure on that bundle (viewed as a real bundle). A weakly-complex manifold (also called a stably (almost) complex manifold) is a real manifold with a complex structure on its stable normal bundle; i.e. if  denotes the normal bundle of
denotes the normal bundle of 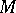 , then there is a complex structure defined on some
, then there is a complex structure defined on some 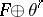 where
where 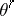 stands for the trivial
stands for the trivial  -dimensional bundle over
-dimensional bundle over 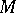 ,
, 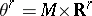 . The complex bordism groups of a space
. The complex bordism groups of a space 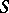 , often denoted by
, often denoted by 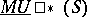 , can now also be interpreted as cobordism classes of mappings
, can now also be interpreted as cobordism classes of mappings 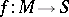 where
where 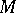 is a weakly-complex manifold without boundary. There is a similar interpretation of the complex cobordism groups
is a weakly-complex manifold without boundary. There is a similar interpretation of the complex cobordism groups 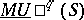 , cf. [a3], and for other bordism and cobordism group.
, cf. [a3], and for other bordism and cobordism group.
The relation between cobordism theory (and other (generalized) cohomology theories) and formal group theory comes about as follows. A generalized cohomology theory 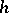 is complex oriented if it has first Chern classes (in a suitable sense; cf. above and [a1], p. 121; [a5], Part II, (2.1)). Let
is complex oriented if it has first Chern classes (in a suitable sense; cf. above and [a1], p. 121; [a5], Part II, (2.1)). Let 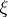 be the class of the canonical line bundle
be the class of the canonical line bundle 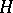 over
over 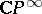 , the space of lines in
, the space of lines in 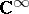 (the fibre of
(the fibre of 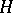 at
at 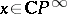 is the line
is the line  ). Then
). Then 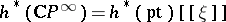 and
and  . Because
. Because 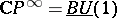 is classifying for complex line bundles, there is an
is classifying for complex line bundles, there is an 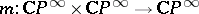 such that
such that 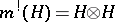 and this induces a ring homomorphism
and this induces a ring homomorphism  . The image of
. The image of  is a power series in two variables, here denoted by
is a power series in two variables, here denoted by 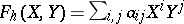 ,
, 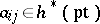 , where
, where 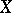 stands for
stands for 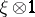 and
and 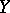 for
for 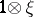 . Equivalently,
. Equivalently, 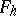 is the power series with coefficients in
is the power series with coefficients in 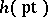 such that
such that 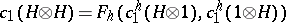 . The power series
. The power series 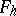 defines a formal group law.
defines a formal group law.
Conversely, the question arises whether every (one-dimensional commutative) formal group arises as the formal group of a generalized cohomology theory. Here the study of (co)bordism of manifolds with special singularities is important.
It turns out (D. Quillen [a4], cf. also [a12]) that for 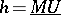 this formal group law
this formal group law 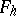 is a universal formal group law. This universality property shows up in topological terms in the form of the theorem that if
is a universal formal group law. This universality property shows up in topological terms in the form of the theorem that if  is any complex oriented generalized cohomology theory, then there is a unique transformation of cohomology theories
is any complex oriented generalized cohomology theory, then there is a unique transformation of cohomology theories  (linear, degree preserving and multiplicative) such that
(linear, degree preserving and multiplicative) such that 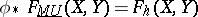 , where
, where 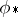 means: apply
means: apply 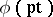 to the coefficients of
to the coefficients of 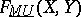 . The logarithm of the formal group law
. The logarithm of the formal group law 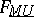 can be calculated (A.S. Mishchenko, cf. [a12]; cf. Formal group for the notion of logarithm of a formal group law). It is equal to
can be calculated (A.S. Mishchenko, cf. [a12]; cf. Formal group for the notion of logarithm of a formal group law). It is equal to
 |
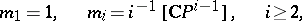 |
where 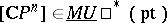 denotes the complex cobordism class of the complex projective space of (complex) dimension
denotes the complex cobordism class of the complex projective space of (complex) dimension  .
.
On the other hand it is possible to write down explicit formulas for the logarithm of a universal formal group law over 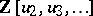 , cf. [a2], Chapt. 1. There result explicit formulas for the polynomial generators of
, cf. [a2], Chapt. 1. There result explicit formulas for the polynomial generators of 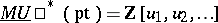 in terms of the
in terms of the 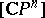 . These formulas take a particularly useful form for the "p-typical" version
. These formulas take a particularly useful form for the "p-typical" version 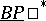 of the cohomology theory
of the cohomology theory 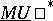 . The generalized cohomology theory
. The generalized cohomology theory 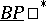 , Brown–Peterson cohomology for a prime number
, Brown–Peterson cohomology for a prime number 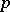 , cf. [a6], is defined by a spectrum
, cf. [a6], is defined by a spectrum 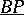 and is such that
and is such that 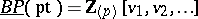 with
with 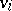 of degree
of degree 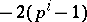 . It is such that
. It is such that 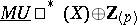 is a direct sum of (dimension shifted) copies of
is a direct sum of (dimension shifted) copies of 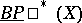 for each space
for each space 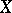 , functorially in
, functorially in 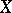 . Here
. Here 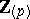 stands for the ring of integers localized at
stands for the ring of integers localized at 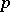 , i.e.
, i.e. 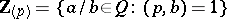 . The theory
. The theory 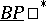 can also be defined as the image of an idempotent cohomology operator
can also be defined as the image of an idempotent cohomology operator 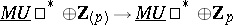 (cf., e.g., [a1], Chapt. 4). This operation corresponds to
(cf., e.g., [a1], Chapt. 4). This operation corresponds to 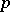 -typification in formal group theory. The Hazewinkel generators ([a1], pp. 137, 369-370)
-typification in formal group theory. The Hazewinkel generators ([a1], pp. 137, 369-370) 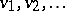 of
of 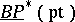 are defined recursively by
are defined recursively by
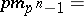 |
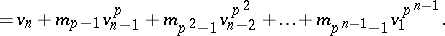 |
They arise from the explicit construction of a 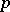 -typical universal formal group [a8]. A different set of generators
-typical universal formal group [a8]. A different set of generators 
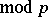 has been given by S. Araki [a7], the Araki generators.
has been given by S. Araki [a7], the Araki generators.
In a certain precise sense, 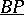 -theory is
-theory is 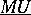 -theory for one prime at the time, and currently a great deal of complex cobordism theory is written in terms of
-theory for one prime at the time, and currently a great deal of complex cobordism theory is written in terms of 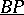 rather than
rather than 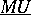 itself. Combined with the theory of cohomology operations, formal group theory (the rings of operations
itself. Combined with the theory of cohomology operations, formal group theory (the rings of operations 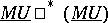 and
and 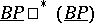 of
of 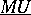 and
and 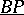 also have interpretations in terms of formal groups, cf. [a1], [a9], [a10]), and spectral sequences, notably the Adams–Novikov spectral sequence and the chromatic spectral sequence (cf. [a1], [a11]), complex cobordism and Brown–Peterson cohomology have become a strong calculation tool in algebraic topology, e.g. for the stable homotopy groups of the spheres.
also have interpretations in terms of formal groups, cf. [a1], [a9], [a10]), and spectral sequences, notably the Adams–Novikov spectral sequence and the chromatic spectral sequence (cf. [a1], [a11]), complex cobordism and Brown–Peterson cohomology have become a strong calculation tool in algebraic topology, e.g. for the stable homotopy groups of the spheres.
References
| [a1] | D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , Acad. Press (1986) |
| [a2] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) |
| [a3] | D. Quillen, "Elementary proofs of some results of cobordism theory using Steenrod operations" Adv. Math. , 7 (1971) pp. 29–56 |
| [a4] | D. Quillen, "On the formal group laws of unoriented and complex cobordism theory" Bull. Amer. Math. Soc , 75 (1969) pp. 1293–1298 |
| [a5] | J.F. Adams, "Stable homotopy and generalised homology" , Univ. Chicago Press (1974) pp. Part III, Chapt. 12 |
| [a6] | E.H. Brown, F.P. Peterson, "A spectrum whose 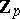 cohomology is the algebra of reduced cohomology is the algebra of reduced 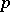 -th powers" Topology , 5 (1966) pp. 149–154 -th powers" Topology , 5 (1966) pp. 149–154 |
| [a7] | S. Araki, "Typical formal groups in complex cobordism and 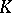 -theory" , Kinokuniya (1973) -theory" , Kinokuniya (1973) |
| [a8] | M. Hazewinkel, "Constructing formal groups III: applications to complex cobordism and Brown–Peterson cohomology" J. Pure Appl. Algebra , 10 (1977) pp. 1–18 |
| [a9] | P.S. Landweber, " and typical formal groups" Osaka J. Math. , 12 (1975) pp. 357–363 and typical formal groups" Osaka J. Math. , 12 (1975) pp. 357–363 |
| [a10] | P.S. Landweber, "Invariant regular ideals in Brown–Peterson cohomology" Duke Math. J. , 42 (1975) pp. 499–505 |
| [a11] | H.R. Miller, D.C. Ravenel, W.S. Wilson, "Periodic phenomena of the Adams–Novikov spectral sequence" Ann. of Math. , 106 (1977) pp. 469–516 |
| [a12] | V.M. Bukhshtaber, A.S. Mishchenko, S.P. Novikov, "Formal groups and their role in the apparatus of algebraic topology" Russ. Math. Surveys , 26 (1971) pp. 63–90 Uspekhi Mat. Nauk , 26 (1971) pp. 131–154 |
Cobordism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cobordism&oldid=16874