Chain geometry
An incidence system constructed by means of an algebra. Originally (1842), Ch. von Staudt defined, on the projective line/plane over  , a chain ( "Kette" ) in a synthetic way as a subline/plane over
, a chain ( "Kette" ) in a synthetic way as a subline/plane over  . Much later, in 1973, W. Benz [a1] gave a common frame for rather different phenomena (the geometries of Möbius, Laguerre and Lie, and Minkowsky; cf. Benz plane) using the concept of a geometry over an algebra. A recent survey of the development of this theory is [a3].
. Much later, in 1973, W. Benz [a1] gave a common frame for rather different phenomena (the geometries of Möbius, Laguerre and Lie, and Minkowsky; cf. Benz plane) using the concept of a geometry over an algebra. A recent survey of the development of this theory is [a3].
Fundamental concepts.
Let  be a ring (associative with one) and let
be a ring (associative with one) and let  be its group of units. To define the projective line
be its group of units. To define the projective line  over
over  , one introduces an equivalence relation
, one introduces an equivalence relation  on
on  , as for the projective straight line over a skew-field:
, as for the projective straight line over a skew-field:
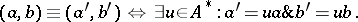 |
Let  denote the equivalence class of
denote the equivalence class of 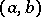 . Then
. Then
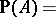 |
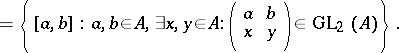 |
One says that 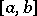 is distant to
is distant to 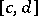 if
if
 |
Let 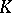 be a commutative ring and
be a commutative ring and  a
a  -algebra, where
-algebra, where  is imbedded in the centre of
is imbedded in the centre of 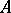 via the mapping
via the mapping  . Regard
. Regard 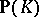 as a subset of
as a subset of 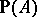 , and define
, and define 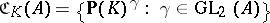 . Then the incidence system
. Then the incidence system 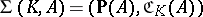 , with
, with  as incidence relation, is called a chain geometry. The elements of
as incidence relation, is called a chain geometry. The elements of 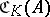 are called chains. Any three pairwise distant points belong to exactly one chain.
are called chains. Any three pairwise distant points belong to exactly one chain. 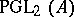 is a group of automorphisms of
is a group of automorphisms of 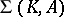 ; it is transitive on the set of triples of pairwise distant points, and hence transitive on the set of chains. Four pairwise distant points belong to a common chain, provided their cross ratio belongs to
; it is transitive on the set of triples of pairwise distant points, and hence transitive on the set of chains. Four pairwise distant points belong to a common chain, provided their cross ratio belongs to 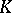 .
.
If 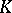 is a field,
is a field,  is said to be a proper chain geometry. A proper chain geometry is a chain space.
is said to be a proper chain geometry. A proper chain geometry is a chain space.
Below, 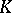 denotes a field.
denotes a field.
Affine case.
Let  . Then
. Then 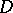 is the set of all points of
is the set of all points of 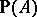 distant to
distant to 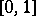 . Consider the traces of the chains in
. Consider the traces of the chains in  :
:
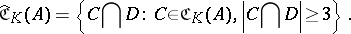 |
There is a natural bijection from  into the affine space
into the affine space  over
over 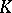 via the mapping
via the mapping 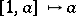 . Under this mapping,
. Under this mapping, 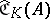 becomes the set
becomes the set
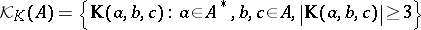 |
of affine chains, defined by
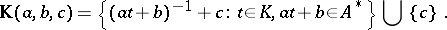 |
This trace geometry is called the affine chain geometry, denoted by 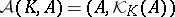 . For
. For  , the set
, the set 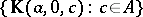 is a bundle of parallel straight lines in the affine space
is a bundle of parallel straight lines in the affine space 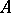 . For an algebraic (especially, finite-dimensional)
. For an algebraic (especially, finite-dimensional)  -algebra
-algebra 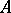 (cf. also Algebraic algebra), the affine chain geometry
(cf. also Algebraic algebra), the affine chain geometry 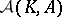 is an affine chain space (cf. Chain space).
is an affine chain space (cf. Chain space).
Structure of morphisms.
Let  ,
,  be
be  -algebras. A
-algebras. A  -Jordan homomorphism
-Jordan homomorphism 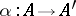 is a
is a  -semi-linear mapping satisfying: i)
-semi-linear mapping satisfying: i) 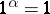 ; and ii) for all
; and ii) for all 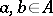 one has
one has  . For a "strong" algebra
. For a "strong" algebra 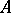 (strongness guarantees a great richness in units for
(strongness guarantees a great richness in units for 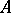 ), any point of
), any point of  can be written as
can be written as 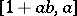 for suitable
for suitable 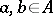 . Then a
. Then a 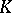 -Jordan homomorphism
-Jordan homomorphism 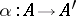 induces a well-defined mapping
induces a well-defined mapping 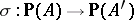 ,
, 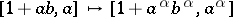 , which preserves pairs of distant points and maps chains to chains. Moreover, under
, which preserves pairs of distant points and maps chains to chains. Moreover, under  :
:  ,
,  ,
,  . Such a mapping is called a fundamental morphism from
. Such a mapping is called a fundamental morphism from 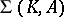 to
to 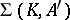 .
.
Conversely, any fundamental morphism 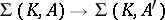 having more than one chain in its image can be obtained in this manner (see [a2] for a more general context).
having more than one chain in its image can be obtained in this manner (see [a2] for a more general context).
Let  be the group of
be the group of  -Jordan automorphisms of
-Jordan automorphisms of  , and let
, and let  be the group of fundamental automorphisms of
be the group of fundamental automorphisms of  . Then
. Then 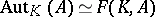 and
and  .
.
Rational representations.
As in the affine case one tries to find kinds of representations for chain geometries  on a part of a projective space where the chains become curves, at least when
on a part of a projective space where the chains become curves, at least when 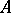 is finite dimensional. In this way one has discovered incidence systems
is finite dimensional. In this way one has discovered incidence systems  isomorphic to
isomorphic to 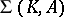 , where
, where 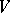 is a projective variety (cf. also Projective scheme),
is a projective variety (cf. also Projective scheme), 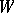 is a (Zariski-) closed subset of
is a (Zariski-) closed subset of  and
and 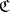 consists of rational curves on
consists of rational curves on  (cf. also Incidence system; Rational curve).
(cf. also Incidence system; Rational curve).
For a  -algebra of
-algebra of  -dimension
-dimension  , a representation of
, a representation of 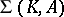 on a part of the Grassmann manifold
on a part of the Grassmann manifold 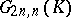 is obtained as follows. For
is obtained as follows. For 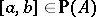 , the set
, the set  is an
is an  -dimensional subspace of the
-dimensional subspace of the 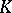 -vector space
-vector space  of dimension
of dimension 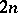 . Then
. Then 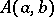 is mapped to a point of
is mapped to a point of 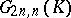 (see Exterior algebra). By this procedure, chains are mapped to normal rational curves of order
(see Exterior algebra). By this procedure, chains are mapped to normal rational curves of order  , i.e., to images of
, i.e., to images of 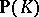 under the Veronese mapping
under the Veronese mapping 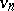 , and
, and 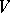 is the intersection of
is the intersection of 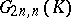 with a linear subspace. Other examples can be obtained from this by suitable projection.
with a linear subspace. Other examples can be obtained from this by suitable projection.
A quadratic algebra 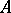 (i.e., any element of
(i.e., any element of 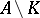 has a quadratic minimal polynomial; cf. also Extension of a field) has a representation as a quadric model (cf. Chain space). Here,
has a quadratic minimal polynomial; cf. also Extension of a field) has a representation as a quadric model (cf. Chain space). Here, 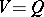 is the quadric and
is the quadric and 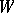 is its set of singular points; the chains are conics.
is its set of singular points; the chains are conics.
 -chain geometries.
-chain geometries.
These are generalizations of chain geometries (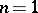 ) to higher dimensions. E.g., let
) to higher dimensions. E.g., let 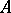 be a quadratic field extension of
be a quadratic field extension of 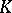 (cf. Extension of a field). Then, in the projective plane over
(cf. Extension of a field). Then, in the projective plane over 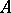 the
the  -chains are the subplanes over
-chains are the subplanes over 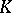 ; these are better known as Baer subplanes, especially in finite geometries (cf. also Geometry).
; these are better known as Baer subplanes, especially in finite geometries (cf. also Geometry).
A Burau geometry is a projective space over  (again a quadratic extension of
(again a quadratic extension of 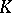 ) together with all projective sublines over
) together with all projective sublines over 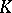 . It can be characterized by the property that the incidence system consisting of a projective line
. It can be characterized by the property that the incidence system consisting of a projective line 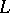 over
over 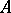 (as a point set) and all sublines over
(as a point set) and all sublines over 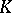 contained in
contained in 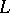 (considered as blocks) for a Möbius plane. A more general concept can be found in [a4].
(considered as blocks) for a Möbius plane. A more general concept can be found in [a4].
References
| [a1] | W. Benz, "Vorlesungen über Geometrie der Algebren" , Springer (1973) |
| [a2] | A. Blunk, "Chain spaces over Jordan systems" Abh. Math. Sem. Hamburg , 64 (1994) pp. 33–49 |
| [a3] | A. Herzer, "Chain geometries" F. Buekenhout (ed.) , Handbook of Incidence Geometry , North-Holland (1995) |
| [a4] | K. Pieconkowski, "Projektive Räume über Schiefkörperpaaren" , W und T, Wiss.- und Technik-Verl. (1994) |
Chain geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chain_geometry&oldid=18056