Caustic
The envelope of rays reflected or refracted by a given curve. The caustic of reflected rays is called a catacaustic, that of refracted rays — a diacaustic.
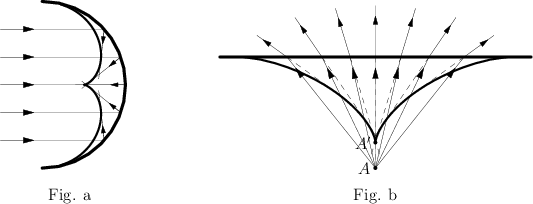
For example, the catacaustic of a parallel beam of rays reflected from a semi-circle is part of an epicycloid (see Fig. a); the diacaustic of a pencil of rays emanating from a point $A$ lying in a denser medium and refracted by a straight line is part of an astroid with cusp $A'$ the distance of which from the line is $1/n$ times that of the point $A$ (where $n$ is the refraction index) (see Fig. b).
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
In terms of purely geometric optics these are curves of light of infinite brightness consisting of points through which infinitely many reflected or refracted light rays pass. In reality they can often be observed as a pattern of pieces of very bright curves. E.g. on a sunny day at the seashore on the bottom beneath a bit of wavy water. Or at the bottom of a cup of tea into which light is shining. Suitably interpreted, caustics are bifurcation sets of elementary catastrophes with 3 control variables. To discuss not only the shape of caustics but also their brightness one needs wave optics and this leads to the study of asymptotic solutions of wave equations and oscillatory integrals [a2], [a3], [a4].
One way of describing the caustic resulting from rays from a point $Q$ reflected by a curve $\gamma$ is as follows. Take a point $T$ on $\gamma$ and draw the tangent $l$; from $Q$ draw the perpendicular to this tangent and let $R$ be the point on the perpendicular on the other side of $l$ at the same distance from $l$ as $Q$. Then the caustic by reflection is the evolute of the curve described by $R$ as $T$ runs over $\gamma$. This result is due to A. Quetelet. It follows readily that the caustic by reflection of the circle is the Pascal limaçon. There is a similar result for a caustic by refraction.
References
| [a1] | G. Salmon, "Higher plane curves" , Hodges, Foster & Figgis (1879) MR0115124 Zbl 05.0341.01 Zbl 05.0340.03 |
| [a2] | J. Chazarain, "Solutions asymptotiques et caustiques" F. Pham (ed.) , Rencontre de Congrès sur les singularités et leurs applications , Univ. Nice (1975) pp. 43–78 |
| [a3] | J.J. Duistermaat, "Oscillatory integrals, Lagrange immersions, and unfolding of singularities" Comm. Pure Appl. Math. , 27 (1974) pp. 207–281 MR0405513 |
| [a4] | T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) pp. Chapt. 12 MR0501079 Zbl 0382.58006 |
| [a5] | J.W. Bruce, P.J. Giblin, "Curves and singularities: a geometrical introduction to singularity theory" , Cambridge Univ. Press (1984) MR1541053 Zbl 0534.58008 |
Caustic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Caustic&oldid=35604