Astroid
A plane algebraic curve of order six, described by a point $M$ on a circle of radius $r$ rolling on the inside of a circle of radius $R=4r$; a hypocycloid with module $m=4$. Its equation in orthogonal Cartesian coordinates is
$$x^{2/3}+y^{2/3}=R^{2/3};$$
and a parametric representation is
$$x=R\cos^3\frac t4,\quad y=R\sin^3\frac t4.$$
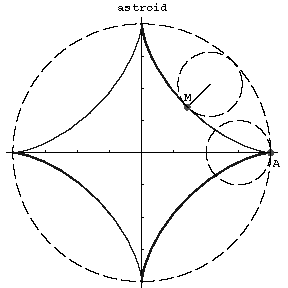
Figure: a013540a
There are four cusps (see Fig.). The length of the arc from the point $A$ is
$$l=\frac32R\sin^2\frac t4.$$
The length of the entire curve is $6R$. The radius of curvature is
$$r_k=\frac32R\sin\frac t2.$$
The area bounded by the curve is
$$S=\frac38\pi R^2.$$
The astroid is the envelope of a family of segments of constant length, the ends of which are located on two mutually perpendicular straight lines. This property of the astroid is connected with one of its generalizations — the so-called oblique astroid, which is the envelope of the segments of constant length with their ends located on two straight lines intersecting at an arbitrary angle.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | E.A. Lockwood, "A book of curves" , Cambridge Univ. Press (1961) |
Astroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Astroid&oldid=53278