Difference between revisions of "Burnside problem"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (bar corrected) |
||
| Line 98: | Line 98: | ||
This is the so-called restricted Burnside problem. It has been positively solved [[#References|[13]]] for all prime exponents $ n = p $. | This is the so-called restricted Burnside problem. It has been positively solved [[#References|[13]]] for all prime exponents $ n = p $. | ||
It has thus been proved that there exists a universal finite $ p $- | It has thus been proved that there exists a universal finite $ p $- | ||
| − | group $ {B(d, p) } | + | group $ \overline{ {B(d, p) }}\; $ |
of order $ b (d, p) $ | of order $ b (d, p) $ | ||
whose quotient groups are isomorphic to all other finite $ p $- | whose quotient groups are isomorphic to all other finite $ p $- | ||
| Line 104: | Line 104: | ||
generators and satisfying the relation $ x ^ {p} = 1 $. | generators and satisfying the relation $ x ^ {p} = 1 $. | ||
If $ B(d, p) $ | If $ B(d, p) $ | ||
| − | is finite, one has the identity $ {B(d, p) } | + | is finite, one has the identity $ \overline{ {B(d, p) }}\; = B(d, p) $. |
A comparison of the results in | A comparison of the results in | ||
| Line 114: | Line 114: | ||
there are only a few estimates from below for $ b(d, p) $, | there are only a few estimates from below for $ b(d, p) $, | ||
connected with corresponding estimates $ c (d, p) $ | connected with corresponding estimates $ c (d, p) $ | ||
| − | for the nilpotency class of the group $ {B(d, p) } | + | for the nilpotency class of the group $ \overline{ {B(d, p) }}\; $. |
It is known that $ c (2, p) $ | It is known that $ c (2, p) $ | ||
cannot be a linear function of $ p $. | cannot be a linear function of $ p $. | ||
More importantly, $ {c } (d, p) $ | More importantly, $ {c } (d, p) $ | ||
| − | increases without limit with $ d $[[#References|[14]]], [[#References|[15]]]. The question of the existence of $ {B (d, n) } | + | increases without limit with $ d $[[#References|[14]]], [[#References|[15]]]. The question of the existence of $ \overline{ {B (d, n) }}\; $ |
for $ n = p ^ {m} $, | for $ n = p ^ {m} $, | ||
$ m > 1 $, | $ m > 1 $, | ||
Revision as of 14:15, 30 May 2020
The Burnside problem for finite groups: Do unsolvable finite groups of odd order exist? Or, in another formulation: Are all finite simple non-Abelian groups of even order? This problem is connected with the name of W. Burnside, who noted in 1897 that all simple non-Abelian groups which were known at that time were of even order [1]. The problem was solved in 1962 by W. Feit and J.G. Thompson [2], who showed that all finite groups of odd order are solvable.
References
| [1] | W. Burnside, "Theory of groups of finite order" , Cambridge Univ. Press (1897) |
| [2] | W. Feit, J.G. Thompson, "Solvability of groups of odd order" Pacific J. Math. , 13 (1964) pp. 775–1029 |
Comments
In [1], Burnside also showed that all groups of order $ p ^ {a} q ^ {b} $, where $ p, q $ are prime numbers and $ a, b \geq 0 $, are solvable.
The Burnside problem for periodic groups: This problem was posed by W. Burnside in 1902 [1]: Is a finitely-generated group, each element of which is of finite order, always finite (the unbounded Burnside problem)? This problem may also be formulated as follows: Are all periodic groups locally finite (cf. Locally finite group)? Burnside himself stressed an important special case of this problem, when the orders of all elements of the groups are bounded uniformly (the bounded Burnside problem), i.e. for a certain natural number $ n $ the identity $ x ^ {n} = 1 $ is valid in the group. It is the bounded variant of the Burnside problem which has received the most attention. In other words, the object studied was the quotient group $ B(d, n) = F/ F ^ {n} $ of a free group $ F $ with $ d \geq 2 $ generators by the smallest normal subgroup $ F ^ {n} $ containing the $ n $- th powers $ f ^ {n} $ of all elements $ f \in F $. The following results are known: $ B(d, 2) $ is an elementary Abelian group of order $ 2 ^ {d} $; $ B(d, 3) $ is a finite group of order $ 3 ^ {m _ {d} } $, where
$$ m _ {d} = \left ( \begin{array}{c} d \\ 1 \end{array} \right ) + \left ( \begin{array}{c} d \\ 2 \end{array} \right ) + \left ( \begin{array}{c} d \\ 3 \end{array} \right ) $$
[1], [2]; $ B(d, 4) $ is a finite group (of order $ 2 ^ {12} $ if $ d = 2 $ and of order $ 2 ^ {69} $ if $ d = 3 $[1], [3], [4]); $ B(d, 6) $ is a finite group of order $ 2 ^ {s} 3 ^ {t} $, where $ s = 1 + (d - 1) 3 ^ {m _ {d} } $, $ t = m _ {r} $ and $ r = 1 + (d-1) 2 ^ {d} $[5], [6]. The negative solution to the bounded Burnside problem was announced in 1959 [7]. The negative solution to the unbounded Burnside problem was published in 1964 [8]. Another construction of a periodic group which is not locally finite was subsequently given [9]. P.S. Novikov and S.I. Adyan
proved in 1968 that the group $ B(d, n) $, $ d \geq 2, $ is infinite for all odd $ n \geq 4381 $( a negative solution of the bounded Burnside problem). It was subsequently shown that the word problem and the conjugation problem for these values of $ d, n $ are solvable in $ B(d, n) $; $ B(d, n) $ cannot be presented by means of a finite number of defining relationships; all finite subgroups in $ B(d, n) $ are Abelian, and all Abelian subgroups are cyclic; $ B(d, n) $, $ d \geq n $, do not meet the maximum or minimum conditions for normal subgroups; the $ B(d, n) $, $ d > 2 $, are isomorphically imbeddable in the group $ B(2, n) $. For a study of the properties of the infinite groups $ B(d, n) $, based on the advanced methods of , see the monograph [11] in which, in particular, the bound on the odd values of $ n $ indicated above is reduced to $ n \geq 665 $. To give a final bound for the indices $ n $ to which correspond finite or infinite groups $ B(d, n) $ is a difficult problem. The values $ n = 5, 12 $, and $ n = 2 ^ {m} $, $ m \geq 3 $, are especially interesting in this context.
In accordance with the idea which has been gradually evolving ever since the middle of the 1930s, the answer to the following question is of importance in the theory of finite groups: Is the order of any finite group with $ d $ generators, obeying the identity relation $ x ^ {n} = 1 $, be bounded from above by a certain natural number $ b(d, n) $, depending only on $ d $ and $ n $? This is the so-called restricted Burnside problem. It has been positively solved [13] for all prime exponents $ n = p $. It has thus been proved that there exists a universal finite $ p $- group $ \overline{ {B(d, p) }}\; $ of order $ b (d, p) $ whose quotient groups are isomorphic to all other finite $ p $- groups with $ d $ generators and satisfying the relation $ x ^ {p} = 1 $. If $ B(d, p) $ is finite, one has the identity $ \overline{ {B(d, p) }}\; = B(d, p) $. A comparison of the results in
and [13] leads to the conclusion that if $ p $ is sufficiently large, there exists a finitely-generated infinite simple $ p $- group of exponent $ p $. It has been shown that $ b(2, 5) = 5 ^ {34} $. For $ p \geq 7 $ there are only a few estimates from below for $ b(d, p) $, connected with corresponding estimates $ c (d, p) $ for the nilpotency class of the group $ \overline{ {B(d, p) }}\; $. It is known that $ c (2, p) $ cannot be a linear function of $ p $. More importantly, $ {c } (d, p) $ increases without limit with $ d $[14], [15]. The question of the existence of $ \overline{ {B (d, n) }}\; $ for $ n = p ^ {m} $, $ m > 1 $, beginning from $ n = 8 $ and 9 is still (1977) open. At the same time, the existence of $ B(d, n) $ for all square-free $ n $ is a consequence of the results reported in [6] and [13], and of the theorem of the solvability of groups of odd-order (cf. Burnside problem for finite groups), and of certain facts concerning the classification of simple groups.
The original solutions [8] of the unbounded Burnside problem and [13] of the restricted Burnside problem are partly based on the theory of algebras — in the former case on the criterion of infinite dimensionality of an algebra, in the latter on an identity of Lie algebras (cf. Lie algebra), which is an analogue of the identity $ x ^ {p} = 1 $ in groups [16], [17]. There are other Burnside-type problems than those mentioned above, and they receive considerable attention [8], [9].
References
| [1] | W. Burnside, "On an unsettled question in the theory of discontinuous groups" Quart. J. Pure Appl. Math. , 33 (1902) pp. 230–238 |
| [2] | F.V. Levi, B.L. van der Waerden, "Ueber eine besondere klasse von Gruppen" Abh. Math. Sem. Univ. Hamburg , 9 (1932) pp. 154–158 |
| [3] | I.N. Sanov, "Solution of the Burnside problem for exponent 4" Uchen. Zap. Leningrad. Gos. Univ. Ser. Mat. , 10 (1940) pp. 166–170 (In Russian) |
| [4] | A.J. Bayes, J. Kautsky, J.W. Wamsley, , Proc. 2-nd Internat. Conf. Theory of Groups , Canberra (1973) pp. 82–89 |
| [5] | M. Hall, "Solution of the Burnside problem for exponent 6" Proc. Nat. Acad. Sci. USA , 43 (1957) pp. 751–753 |
| [6] | P. Hall, G. Higman, "On the 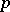 -length of -length of 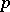 soluble groups and reduction theorems for Burnside's problem" Proc. London Math. Soc. (3) , 6 (1956) pp. 1–42 soluble groups and reduction theorems for Burnside's problem" Proc. London Math. Soc. (3) , 6 (1956) pp. 1–42 |
| [7] | P.S. Novikov, "On periodic groups" Amer. Math. Soc. Transl. , 45 (1965) pp. 19–22 (In Russian) Dokl. Akad. Nauk SSSR , 127 : 4 (1959) pp. 749–752 |
| [8] | E.S. Golod, "On nil algebras and residually-finite groups" Izv. Akad. Nauk SSSR Ser. Mat. , 28 (1964) pp. 273–276 (In Russian) |
| [9] | S.V. Aleshin, "Finite automata and Burnside's problem for periodic groups" Math. Notes , 11 : 3 (1972) pp. 199–203 Mat. Zametki , 11 : 3 (1972) pp. 319–328 |
| [10a] | P.S. Novikov, S.I. Adyan, Izv. Akad. Nauk SSSR Ser. Mat. , 32 : 1 (1968) pp. 212–244 |
| [10b] | P.S. Novikov, S.I. Adyan, Izv. Akad. Nauk SSSR Ser. Mat. , 32 : 3 (1968) pp. 709–731 |
| [11] | S.I. Adyan, "The Burnside problem and identities in groups" , Springer (1979) (Translated from Russian) |
| [12] | O.Yu. Shmidt, , Selected works on mathematics , Moscow (1959) pp. 298–300 (In Russian) |
| [13] | A.I. Kostrikin, "On Burnside's problem" Izv. Akad. Nauk SSSR Ser. Mat. , 23 (1959) pp. 3–34 (In Russian) |
| [14] | S.M. Bachmuth, H.Y. Motuzucki, D.W. Walkup, "A nonsolvable group of exponent 5" Bull. Amer. Math. Soc. , 76 : 3 (1970) pp. 638–640 |
| [15] | Yu.P. Razmyslov, "On Lie algebras satisfying the Engel condition" Algebra and Logic , 10 : 1 (1971) pp. 21–29 Algebra i Logika , 10 : 1 (1971) pp. 33–44 |
| [16] | W. Magnus, "Ueber Beziehungen zwischen höheren Kommutatoren" J. Reine Angew. Math. , 177 (1937) pp. 105–115 |
| [17] | G. Higman, "Lie ring methods in the theory of finite nilpotent groups" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 307–312 |
| [18] | A.G. Kurosh, "Ring-theoretical problems connected with Burnside's problem for periodic groups" Izv. Akad. Nauk SSSR Ser. Mat. , 5 (1941) pp. 233–240 (In Russian) (German abstract) |
A.I. Kostrikin
Comments
A positive solution of the restricted Burnside problem for the case of exponent five was first obtained in [a11]. In the period 1977–1986 a lot of additional results on the Burnside problem for periodic groups were obtained. R.I. Grigorchuk [a1] proposed a most-simple construction of finitely-generated infinite $ p $- groups. One of its versions leads, in particular (cf. [a2]), to the construction of groups of intermediate growth, i.e. neither polynomial, nor exponential growth; it leads, moreover, to the construction of both such periodic groups as well as of such torsion-free groups (solutions to Milnor's problem).
A simple and geometrically obvious version of the negative solution to the bounded Burnside problem for odd numbers $ n > 10 ^ {10} $ was given by A.Yu. Ol'shanskii [a3]. Later (cf. [a4]) he constructed for each sufficiently-large prime number $ p $ an infinite $ p $- group in which all proper subgroups have order $ p $( Tarski's monster). This is the strongest form of a negative solution to Burnside's problem. Everything that has been done on the restricted Burnside problem is summarized in [a5] and the book [a6]. In [a6] a complete list of references is given, as well as results of computer experiments of various scientists:
$ | B (4, 4) | = 2 ^ {422} $( cf. [a7]),
$ | B (3, 5) | \leq 5 ^ {2282} $( cf. [a8]),
$ | B (2, 7) | > 7 ^ {6366} $,
$ | B (2, 5) | = 5 ^ {34} $( cf. [a9]).
Further, [a10] may prove to be useful.
References
| [a1] | R.I. Grigorchuk, "On Burnside's problem for periodic groups" Funktsional. Anal. i Prilozhen. , 14 : 1 (1980) pp. 53–54 (In Russian) |
| [a2] | R.I. Grigorchuk, "Milnor's problem on the growth of groups" Dokl. Akad. Nauk SSSR , 271 : 1 (1983) pp. 30–33 (In Russian) |
| [a3] | A.Yu. Ol'shanskii, "On a theorem of Novikov–Adyan" Mat. Sb. , 118 : 2 (1982) pp. 202–235 (In Russian) |
| [a4] | A.Yu. Ol'shanskii, "Groups of bounded period in which all subgroups are of prime order" Algebra i Logika , 21 : 5 (1982) pp. 555–618 (In Russian) |
| [a5] | M.R. Vaughan-Lee, "The restricted Burnside problem" Bull. London Math. Soc. , 17 (1985) pp. 113–133 |
| [a6] | A.I. Kostrikin, "Around Burnside" , Springer (1989) (Translated from Russian) |
| [a7] | W.A. Alford, G. Havas, M.F. Newman, "Groups of exponent four" Notices Amer. Math. Soc. , 22 (1975) pp. A.301 |
| [a8] | G. Havas, M.F. Newman, M.R. Vaughan-Lee, "A nilpotent quotient algorithm for graded Lie rings" To appear |
| [a9] | G. Havas, G.E. Wall, J.W. Wamsley, "The two-generator restricted Burnside group of order five" Bull. Austral. Math. Soc. , 10 (1974) pp. 459–470 |
| [a10] | J.L. Mennicke (ed.) , Proc. Burnside workshop Bielefeld, 1977 , Lect. notes in math. , 806 , Springer (1980) |
| [a11] | G. Higman, "On finite groups of exponent five" Proc. Cambridge Phil. Soc , 52 (1956) pp. 381–390 |
Burnside problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Burnside_problem&oldid=46210