Difference between revisions of "Arbitration scheme"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing spaces) |
||
| Line 14: | Line 14: | ||
be the set of outcomes, let $ d = ( d _ {1} \dots d _ {n} ) $ | be the set of outcomes, let $ d = ( d _ {1} \dots d _ {n} ) $ | ||
be the status quo point, i.e. the point corresponding to the situation in which no cooperative outcome is realized, let $ [ R, d ] $ | be the status quo point, i.e. the point corresponding to the situation in which no cooperative outcome is realized, let $ [ R, d ] $ | ||
| − | be the corresponding arbitration game and let $ \overline{u} | + | be the corresponding arbitration game and let $ \overline{u} $ |
be an arbitration solution of it. An outcome $ u ^ {*} $ | be an arbitration solution of it. An outcome $ u ^ {*} $ | ||
is called a Nash solution if | is called a Nash solution if | ||
| Line 24: | Line 24: | ||
Only a Nash solution satisfies the following axioms: 1) if $ f $ | Only a Nash solution satisfies the following axioms: 1) if $ f $ | ||
| − | is a linear non-decreasing mapping then $ f \overline{u} | + | is a linear non-decreasing mapping then $ f \overline{u} $ |
| − | is an arbitration solution of the game $ [ fR, fd ] $( | + | is an arbitration solution of the game $ [ fR, fd ] $ (invariance with respect to utility transformations); 2) $ \overline{u} \geq d $, |
| − | invariance with respect to utility transformations); 2) $ \overline{u} | + | $ \overline{u} \in R $ |
| − | $ \overline{u} | ||
and there is no $ u \in R $ | and there is no $ u \in R $ | ||
| − | such that $ u \geq \overline{u} | + | such that $ u \geq \overline{u} $ (Pareto optimality); 3) if $ R ^ \prime \subset R $, |
| − | Pareto optimality); 3) if $ R ^ \prime \subset R $, | ||
$ d ^ \prime = d $, | $ d ^ \prime = d $, | ||
| − | $ \overline{u} | + | $ \overline{u} \in R ^ \prime $, |
| − | then $ \overline{u} | + | then $ \overline{u} ^ \prime = \overline{u} $ (independence of irrelevant alternatives); and 4) if $ d _ {i} = d _ {j} $, |
| − | independence of irrelevant alternatives); and 4) if $ d _ {i} = d _ {j} $, | ||
$ i, j = 1 \dots n $, | $ i, j = 1 \dots n $, | ||
and $ R $ | and $ R $ | ||
| − | is symmetric, then $ \overline{u} | + | is symmetric, then $ \overline{u} _ {i} = \overline{u} _ {j} $, |
| − | $ i, j = 1 \dots n $( | + | $ i, j = 1 \dots n $ (symmetry). |
| − | symmetry). | ||
| − | Another arbitration scheme for an $ n $- | + | Another arbitration scheme for an $ n $-person game with characteristic function $ v $ |
| − | person game with characteristic function $ v $ | ||
and player set $ N = \{ 1 \dots n \} $ | and player set $ N = \{ 1 \dots n \} $ | ||
was given by L.S. Shapley [[#References|[2]]]. The Shapley solution $ \phi (v) = ( \phi _ {1} (v) \dots \phi _ {n} (v) ) $, | was given by L.S. Shapley [[#References|[2]]]. The Shapley solution $ \phi (v) = ( \phi _ {1} (v) \dots \phi _ {n} (v) ) $, | ||
| Line 63: | Line 58: | ||
The arbitration schemes of Nash and Shapley were generalized by J.C. Harsanyi [[#References|[4]]]. A Harsanyi solution satisfies, apart from the four axioms of Nash, the two axioms: 1) the solution depends monotonically on the initial demands of the players; and 2) if $ u ^ {*} $ | The arbitration schemes of Nash and Shapley were generalized by J.C. Harsanyi [[#References|[4]]]. A Harsanyi solution satisfies, apart from the four axioms of Nash, the two axioms: 1) the solution depends monotonically on the initial demands of the players; and 2) if $ u ^ {*} $ | ||
and $ u ^ {**} $ | and $ u ^ {**} $ | ||
| − | are two solutions, then $ \overline{u} | + | are two solutions, then $ \overline{u} $, |
defined by | defined by | ||
$$ | $$ | ||
| − | \overline{u} | + | \overline{u} \geq \mathop{\rm min} _ {i \in N } |
( u _ {i} ^ {*} , u _ {i} ^ {**} ) , | ( u _ {i} ^ {*} , u _ {i} ^ {**} ) , | ||
$$ | $$ | ||
| − | is also a solution if and only if $ \overline{u} | + | is also a solution if and only if $ \overline{u} $ |
belongs to the boundary of the set $ R $. | belongs to the boundary of the set $ R $. | ||
Revision as of 07:10, 21 June 2022
A rule by which each arbitration game (cf. Cooperative game) is put into correspondence with a unique outcome of the game is called an arbitration solution. The first arbitration scheme was considered by J. Nash [1] for the case of a two-person game. Let $ R= \{ u = ( u _ {1} \dots u _ {n} ) \} $
be the set of outcomes, let $ d = ( d _ {1} \dots d _ {n} ) $
be the status quo point, i.e. the point corresponding to the situation in which no cooperative outcome is realized, let $ [ R, d ] $
be the corresponding arbitration game and let $ \overline{u} $
be an arbitration solution of it. An outcome $ u ^ {*} $
is called a Nash solution if
$$ \prod _ { i } ( u _ {i} ^ {*} - d _ {i} ) = \max _ {u \in R } \prod _ { i } ( u _ {i} - d _ {i} ) . $$
Only a Nash solution satisfies the following axioms: 1) if $ f $ is a linear non-decreasing mapping then $ f \overline{u} $ is an arbitration solution of the game $ [ fR, fd ] $ (invariance with respect to utility transformations); 2) $ \overline{u} \geq d $, $ \overline{u} \in R $ and there is no $ u \in R $ such that $ u \geq \overline{u} $ (Pareto optimality); 3) if $ R ^ \prime \subset R $, $ d ^ \prime = d $, $ \overline{u} \in R ^ \prime $, then $ \overline{u} ^ \prime = \overline{u} $ (independence of irrelevant alternatives); and 4) if $ d _ {i} = d _ {j} $, $ i, j = 1 \dots n $, and $ R $ is symmetric, then $ \overline{u} _ {i} = \overline{u} _ {j} $, $ i, j = 1 \dots n $ (symmetry).
Another arbitration scheme for an $ n $-person game with characteristic function $ v $ and player set $ N = \{ 1 \dots n \} $ was given by L.S. Shapley [2]. The Shapley solution $ \phi (v) = ( \phi _ {1} (v) \dots \phi _ {n} (v) ) $, where
$$ \phi _ {i} (v) = \sum _ {S \subset N } \gamma _ {n} (s) [ v (S) -v ( S \setminus \{ i \} ) ] , $$
$ \gamma _ {n} (s) = (s-1) ! (n-s) ! / n ! $ and $ s $ is the number of elements of the set $ S $, also satisfies the axiom of symmetry, but, moreover, $ \sum _ {i} \phi _ {i} (v) = v (N) $, and for any two games $ u $ and $ v $ the equality $ \phi (u+v) = \phi (u) + \phi (v) $ holds. Arbitration schemes with interpersonal utility comparisons have also been considered [3].
The arbitration schemes of Nash and Shapley were generalized by J.C. Harsanyi [4]. A Harsanyi solution satisfies, apart from the four axioms of Nash, the two axioms: 1) the solution depends monotonically on the initial demands of the players; and 2) if $ u ^ {*} $ and $ u ^ {**} $ are two solutions, then $ \overline{u} $, defined by
$$ \overline{u} \geq \mathop{\rm min} _ {i \in N } ( u _ {i} ^ {*} , u _ {i} ^ {**} ) , $$
is also a solution if and only if $ \overline{u} $ belongs to the boundary of the set $ R $.
Under suitable conditions an arbitration scheme depends continuously on the parameters of the game.
References
| [1] | J. Nash, "The bargaining problem" Econometrica , 18 : 2 (1950) pp. 155–162 |
| [2] | L.S. Shapley, "A value for  -person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 -person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 |
| [3] | H. Raiffa, "Arbitration schemes for generalized two-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 361–387 |
| [4] | J.C. Harsanyi, "A bargaining model for the cooperative  -person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 4 , Princeton Univ. Press (1959) pp. 325–355 -person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 4 , Princeton Univ. Press (1959) pp. 325–355 |
Comments
Arbitration schemes are also called bargaining schemes and a Nash solution is also called a bargaining solution. The Shapley solution vector $ \phi $ is also called the Shapley value. For other, more recent, bargaining schemes, such as the Kalai–Smorodinsky solution and Szidarovsky's generalization of the concept of a Nash solution, the reader is referred to [a1], [a2], respectively [a6]. For further developments concerning Harsanyi solutions, cf. [a3]. Some authors distinguish between bargaining schemes and arbitration schemes. Then the Nash scheme is a bargaining scheme and the Shapley one an arbitration scheme, [a5].
References
| [a1] | E. Kalai, M. Smorodinsky, "Other solutions to Nash's bargaining problems" Econometrica , 43 (1975) pp. 513–518 |
| [a2] | A.E. Roth, "Axiomatic models of bargaining" , Lect. notes econom. and math. systems , 170 , Springer (1979) |
| [a3] | J.C. Harsanyi, "Papers in game theory" , Reidel (1982) |
| [a4] | R.J. Aumann, L.S. Shapley, "Values of non-atomic games" , Princeton Univ. Press (1974) |
| [a5] | A. Rapoport, "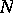 -person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168 -person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168 |
| [a6] | J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199 |
| [a7] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
Arbitration scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arbitration_scheme&oldid=52469