Approximation of functions of a complex variable
The branch of complex analysis studying problems regarding the approximate representation (approximation) of functions of a complex variable by means of analytic functions of a specific class. The fundamental problems in the theory of approximation of functions of a complex variable are: the possibility of approximating; the rate of approximation; and the approximation properties of various methods of representing functions (interpolation sequences and series, series in orthogonal polynomials or Faber polynomials, expansion in continued fractions and Padé approximation, sequences of polynomials in exponential functions, Dirichlet series, etc.). The theory of approximation of functions of a complex variable is intimately connected with other branches of complex analysis, and with mathematics in general. Methods and results on conformal mapping, integral representation, potential theory, the theory of function algebras, etc., play an important role in approximation theory.
The central problems in the theory of approximation of functions of a complex variable relate to approximation by polynomials or rational functions, in particular by polynomials and rational functions of best approximation (existence, characteristic properties, uniqueness), as well as to extremal problems and various estimates for polynomials and rational functions (growth estimates, inequalities for derivatives, polynomials and rational functions, least deviation from zero, etc.).
A.A. Gonchar
The approximation of functions of a complex variable by polynomials and rational functions.
In this branch of approximation theory one may distinguish several directions.
1) The study of the possibility of approximating a function 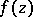 of a complex variable
of a complex variable  with given accuracy by polynomials or rational functions in
with given accuracy by polynomials or rational functions in  , in dependence on the properties of the set
, in dependence on the properties of the set 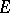 on which
on which 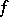 is given and on which
is given and on which 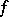 is to be approximated, on the properties of the metric
is to be approximated, on the properties of the metric 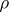 of deviation and on the properties of
of deviation and on the properties of 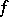 itself.
itself.
2) The study of the properties of polynomials and rational functions of best approximation, i.e. polynomials 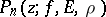 and rational functions
and rational functions 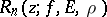 of degree not exceeding
of degree not exceeding  ,
, 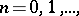 for which
for which
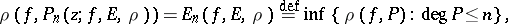 |
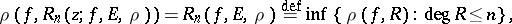 |
where the infima are over the set of polynomials 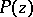 of degree
of degree 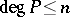 or rational functions
or rational functions 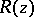 of degree
of degree 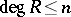 , respectively (or over parts of these sets, distinguished by addition requirements). In fact, one deals here with properties of solutions for a certain class of extremal problems. In this context one may also consider the study of other extremal problems on sets of polynomials, rational functions and on certain classes of analytic functions, as well as the study of analytic properties of polynomials and rational functions (in particular, obtaining inequalities between various norms of these functions and their derivatives).
, respectively (or over parts of these sets, distinguished by addition requirements). In fact, one deals here with properties of solutions for a certain class of extremal problems. In this context one may also consider the study of other extremal problems on sets of polynomials, rational functions and on certain classes of analytic functions, as well as the study of analytic properties of polynomials and rational functions (in particular, obtaining inequalities between various norms of these functions and their derivatives).
3) The study of the dependence of the rate of decrease (to zero) of  and
and 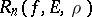 , as
, as 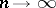 , on the properties of
, on the properties of 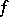 ,
, 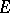 and
and 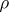 (the so-called direct theorems of approximation theory) and the dependence of the properties of
(the so-called direct theorems of approximation theory) and the dependence of the properties of 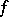 on the rate of decrease of
on the rate of decrease of 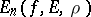 and
and 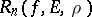 to zero as
to zero as 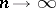 and on the properties of
and on the properties of 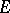 and
and 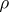 (inverse theorems). The study of approximation properties of well-known methods in approximation theory (e.g., series in Faber polynomials, various interpolation processes (cf. Interpolation process)), as well as the search for new effective approximation methods are related to this direction.
(inverse theorems). The study of approximation properties of well-known methods in approximation theory (e.g., series in Faber polynomials, various interpolation processes (cf. Interpolation process)), as well as the search for new effective approximation methods are related to this direction.
4) The approximation of functions of several complex variables. Here, basically, the same problems are solved as in the case of one complex variable, but the results and the methods for obtaining them differ, as a rule, sharply from those used in the case of one variable.
In the following some basic results have been listed.
1) The problem of the existence of a uniform approximation by polynomials that is as good as one pleases is solved by the Runge theorem (if 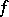 is analytic on
is analytic on 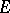 ), the Lavrent'ev theorem (if
), the Lavrent'ev theorem (if 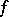 is continuous on
is continuous on 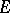 ), the Keldysh theorem (if
), the Keldysh theorem (if 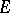 is a closed domain,
is a closed domain, 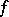 is continuous on
is continuous on 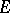 and analytic within
and analytic within 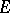 ) and the Mergelyan theorem (in the general case:
) and the Mergelyan theorem (in the general case: 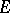 is a compact set,
is a compact set, 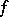 is continuous on
is continuous on 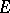 and analytic at interior points of
and analytic at interior points of 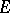 ).
).
2) The problem whether it is possible to approximate holomorphic functions on closed sets 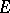 in the extended complex plane
in the extended complex plane 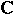 is solved by Runge's theorem. In the study of approximating a function
is solved by Runge's theorem. In the study of approximating a function 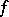 in various spaces, using the metric of these spaces, by rational functions, an important role is played by characteristics of the set
in various spaces, using the metric of these spaces, by rational functions, an important role is played by characteristics of the set 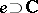 analogous to the analytic capacity
analogous to the analytic capacity 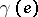 . In terms of
. In terms of 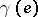 the problem of the description of all compact sets
the problem of the description of all compact sets 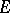 on which any continuous function can be approximated with arbitrary accuracy by rational functions is solved as follows: It is necessary and sufficient that either
on which any continuous function can be approximated with arbitrary accuracy by rational functions is solved as follows: It is necessary and sufficient that either
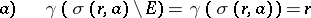 |
for any disc 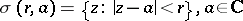 ,
, 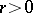 ; or that
; or that
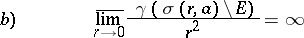 |
for any 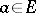 (the equivalence of a) and b) expresses the so-called "instability" of the analytic capacity).
(the equivalence of a) and b) expresses the so-called "instability" of the analytic capacity).
3) If 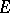 is bounded and Lebesgue-measurable and if
is bounded and Lebesgue-measurable and if 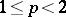 , then the set of all rational functions is dense in
, then the set of all rational functions is dense in 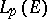 .
.
4) If 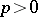 and if
and if 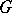 is a simply-connected domain with a rectifiable Jordan boundary, then the family of all polynomials in
is a simply-connected domain with a rectifiable Jordan boundary, then the family of all polynomials in  is dense in the Smirnov class
is dense in the Smirnov class 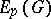 if and only if
if and only if 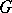 is a Smirnov domain.
is a Smirnov domain.
5) Let the complex-valued functions 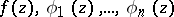 ,
, 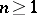 , be continuous on a compact set
, be continuous on a compact set 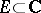 . Among all generalized polynomials
. Among all generalized polynomials
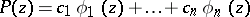 |
( are arbitrary complex numbers) a generalized polynomial
are arbitrary complex numbers) a generalized polynomial 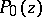 deviates least from
deviates least from 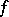 in the metric
in the metric
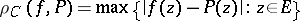 |
if and only if
 |
 |
for each 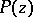 .
.
6) If 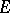 is a compact set with connected complement
is a compact set with connected complement 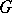 and if
and if 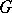 has a Green function (for the first boundary value problem for the Laplace equation)
has a Green function (for the first boundary value problem for the Laplace equation) 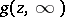 with a pole at
with a pole at 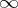 , then for each
, then for each 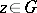 and each polynomial
and each polynomial 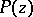 of degree
of degree  , the inequality
, the inequality
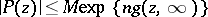 |
with 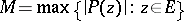 holds.
holds.
7) If 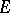 is a bounded non-degenerate continuum with connected complement
is a bounded non-degenerate continuum with connected complement 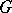 and if
and if 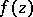 is analytic at interior points of
is analytic at interior points of 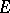 and continuous on
and continuous on 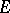 with modulus of continuity
with modulus of continuity 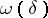 , then
, then
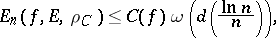 |
where
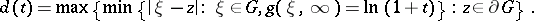 |
If the closed domain 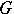 is bounded by an analytic curve
is bounded by an analytic curve 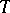 , then the condition
, then the condition
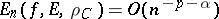 |
is equivalent to the condition that 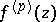 is Hölder continuous of order
is Hölder continuous of order 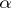 ,
, 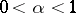 , in
, in 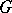 . The case when
. The case when 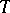 is a piecewise-smooth curve with corners has been studied.
is a piecewise-smooth curve with corners has been studied.
8) In a number of cases for the approximation of analytic functions various interpolation processes prove effective, including Padé approximation and its generalizations.
9) For 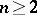 , in
, in 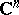 there exist both non-closed Jordan curves on which not every continuous function can be uniformly approximated by polynomials in
there exist both non-closed Jordan curves on which not every continuous function can be uniformly approximated by polynomials in 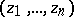 to any degree of accuracy, and closed Jordan curves on which polynomials uniformly approximate any continuous function. In
to any degree of accuracy, and closed Jordan curves on which polynomials uniformly approximate any continuous function. In 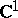 this is impossible.
this is impossible.
10) Up till now (1983) there are comparatively few direct theorems on the approximation by rational functions with free poles (i.e. without any condition on the position of the poles of the approximating functions) and a considerable amount of inverse theorems.
References
| [1] | V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian) |
| [2] | J.L. Walsh, "Interpolation and approximation by rational functions in the complex domain" , Amer. Math. Soc. (1969) |
| [3] | V.I. Smirnov, A.N. Lebedev, "Functions of a complex variable: constructive theory" , M.I.T. (1968) (Translated from Russian) |
| [4] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
| [5] | V.N. Rusak, "Rational functions as approximating tool" , Minsk (1979) (In Russian) |
| [6] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
| [7] | A.F. Leont'ev, "Exponential series" , Moscow (1976) (In Russian) |
| [8] | , Some questions in approximation theory , Moscow (1963) (In Russian; translated from English) |
| [9] | M.V. Keldysh, Dokl. Akad. Nauk SSSR , 4 (1936) pp. 163–166 |
| [10] | M. [M.A. Lavrent'ev] Lafrientieff, "Zur Theorie der konformen Abbildung" Trudy Mat. Inst. Steklov. , 5 (1934) pp. 159–245 |
| [11] | A.N. Kolmogorov, "Remark on the polynomials of P.L. Chebyshev deviating least from a given function" Uspekhi Mat. Nauk , 3 : 1 (1948) pp. 216–221 (In Russian) |
| [12] | S.N. Mergelyan, "Uniform approximation to functions of a complex variable" Series and approximation , 3 , Amer. Math. Soc. (1962) pp. 294–391 Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 31–122 |
| [13] | A.G. Vitushkin, "The analytic capacity of sets in problems of approximation theory" Russian Math. Surveys , 22 (1967) pp. 167–200 Uspekhi Mat. Nauk , 22 : 6 (1967) pp. 141–199 |
| [14] | M.M. Dzhrbasyan, "Some questions of the theory of weighted polynomials in a complex domain" Mat. Sb. , 36 (1955) pp. 353–440 (In Russian) |
| [15] | A.A. Gonchar, "The rate of approximation of functions by rational numbers and properties of numbers" , Proc. Internat. Congress Mathematicians (Moscow, 1966) , Mir (1968) pp. 329–356 (In Russian) |
| [16] | E.P. Dolzhenko, P.L. Ul'yanov, Vestn. Moskov. Univ. Ser. Mat. Mekh. , 1 (1980) pp. 3–13 |
| [17] | S.N. Mergelyan, "On the approximation of functions of a complex variable" , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) pp. 383–398 (In Russian) |
| [18] | A.A. Gonchar, S.N. Mergelyan, , History of paternal mathematics , 1 , Kiev (1970) pp. 112–193 (In Russian) |
| [19] | P.M. Tamrazov, "Smoothness and polynomial approximation" , Kiev (1975) (In Russian) |
| [20] | M.S. Mel'nikov, S.O. Sinanyan, , Contemporary problems in mathematics , 4 , Moscow (1975) pp. 143–250 (In Russian) |
E.P. Dolzhenko
Comments
Let 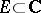 be a compact set. Let
be a compact set. Let 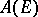 denote the set of functions
denote the set of functions  that are continuous on
that are continuous on 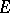 and analytic at interior points (if any) of
and analytic at interior points (if any) of 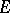 . Denote by
. Denote by 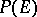 (respectively,
(respectively,  ) the set of functions
) the set of functions 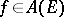 that can be uniformly approximated on
that can be uniformly approximated on 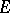 by polynomials (respectively, rational functions). Mergelyan's theorem states: 1)
by polynomials (respectively, rational functions). Mergelyan's theorem states: 1) 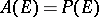 if and only if
if and only if  , the complement of
, the complement of 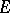 , is connected; 2)
, is connected; 2) 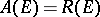 if
if  is finitely-connected. Examples of compact sets
is finitely-connected. Examples of compact sets 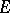 for which
for which 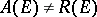 are known (e.g. the Schweizer Käse of A. Roth, cf. [a1]). The problem arises of characterizing those
are known (e.g. the Schweizer Käse of A. Roth, cf. [a1]). The problem arises of characterizing those 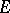 for which
for which 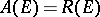 . The solution was given by E. Bishop and A.G. Vitushkin (independently) for compact sets without interior points, and by Vitushkin for general compact
. The solution was given by E. Bishop and A.G. Vitushkin (independently) for compact sets without interior points, and by Vitushkin for general compact 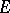 . Vitushkin's theorem can be found in [a1].
. Vitushkin's theorem can be found in [a1].
The sets 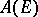 ,
, 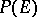 and
and 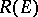 are uniform algebras, e.g. function algebras endowed with the sup-norm (cf. Algebra of functions; Uniform algebra). For studies stressing this aspect see [6] and [a4].
are uniform algebras, e.g. function algebras endowed with the sup-norm (cf. Algebra of functions; Uniform algebra). For studies stressing this aspect see [6] and [a4].
Another direction of research is to study not approximation by linear combinations of 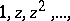 or
or 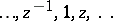 (polynomials or rational functions) but by linear combinations of powers
(polynomials or rational functions) but by linear combinations of powers 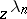 , or of exponentials
, or of exponentials 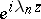 , where
, where 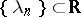 , on sets
, on sets 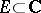 , mostly on curves satisfying some "oscillation condition" . Results of this type related to the Müntz theorem; Lacunary power series; the Paley–Wiener theorem, zero sets of analytic functions, etc. (cf. [a5]).
, mostly on curves satisfying some "oscillation condition" . Results of this type related to the Müntz theorem; Lacunary power series; the Paley–Wiener theorem, zero sets of analytic functions, etc. (cf. [a5]).
In 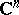 approximation problems depend essentially on the geometry of the domain under consideration (this is related to the so-called Levi problem of characterizing domains of holomorphy). One way to approach approximation problems is via Hörmander's
approximation problems depend essentially on the geometry of the domain under consideration (this is related to the so-called Levi problem of characterizing domains of holomorphy). One way to approach approximation problems is via Hörmander's 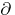 mechanism (cf. [a6]). An example of an approximation theorem is Kerzman's theorem: Let
mechanism (cf. [a6]). An example of an approximation theorem is Kerzman's theorem: Let 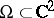 be a strongly pseudo-convex domain with sufficiently smooth boundary (
be a strongly pseudo-convex domain with sufficiently smooth boundary ( suffices). Then every function
suffices). Then every function 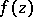 holomorphic on
holomorphic on  and continuous on
and continuous on 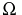 can be uniformly approximated on
can be uniformly approximated on 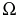 by functions
by functions 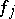 that are holomorphic on some (strongly pseudo-convex) domain
that are holomorphic on some (strongly pseudo-convex) domain 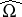 containing
containing 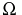 , [a7].
, [a7].
References
| [a1] | D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980) |
| [a2] | R.C. Buck, "Survey of recent Russian literature on approximation" R.E. Langer (ed.) , On numerical approximation , Univ. of Wisconsin Press (1959) pp. 341–359 |
| [a3] | J. Korevaar, "Polynomial and rational approximation in the complex domain" J.G. Clunie (ed.) , Aspects of contemporary complex analysis , Acad. Press (1980) pp. 251–292 |
| [a4] | E.L. Stout, "The theory of uniform algebras" , Bogden & Quigley (1971) |
| [a5] | R.M. Redheffer, "Completeness of sets of complex exponentials" Adv. in Math. , 24 (1977) pp. 1–62 |
| [a6] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Sect. 4.5 |
| [a7] | N. Kerzman, "Hölder and 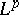 estimates for solutions of estimates for solutions of 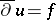 on strongly pseudo-convex domains" Commun. Pure Appl. Math. , 24 (1971) pp. 301–380 on strongly pseudo-convex domains" Commun. Pure Appl. Math. , 24 (1971) pp. 301–380 |
Approximation of functions of a complex variable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_of_functions_of_a_complex_variable&oldid=16822