Analytic group
A set 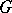 which possesses at the same time the structure of a topological group and that of a finite-dimensional analytic manifold (over a field
which possesses at the same time the structure of a topological group and that of a finite-dimensional analytic manifold (over a field 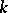 that is complete in some non-trivial norm, cf. Norm on a field) so that the mapping
that is complete in some non-trivial norm, cf. Norm on a field) so that the mapping 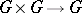 defined by the rule
defined by the rule 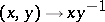 is analytic. An analytic group is always Hausdorff; if
is analytic. An analytic group is always Hausdorff; if 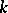 is locally compact, then
is locally compact, then 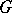 is locally compact. If
is locally compact. If  is, respectively, the field of real, complex or
is, respectively, the field of real, complex or 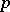 -adic numbers, then
-adic numbers, then 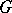 is called a real, complex or
is called a real, complex or 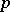 -adic analytic group, respectively. An example of an analytic group is the general linear group
-adic analytic group, respectively. An example of an analytic group is the general linear group 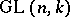 of the vector space
of the vector space 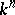 over
over 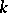 (cf. Linear classical group) or, more generally, the group of invertible elements of an arbitrary finite-dimensional associative algebra with a unit over
(cf. Linear classical group) or, more generally, the group of invertible elements of an arbitrary finite-dimensional associative algebra with a unit over 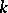 . In general, the group of
. In general, the group of 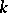 -rational points of an algebraic group, defined over
-rational points of an algebraic group, defined over 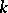 , is an analytic group. A subgroup of an analytic group
, is an analytic group. A subgroup of an analytic group 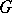 which is a submanifold in
which is a submanifold in 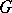 is called an analytic subgroup; such a subgroup must be closed in
is called an analytic subgroup; such a subgroup must be closed in 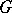 . For example, the orthogonal group
. For example, the orthogonal group 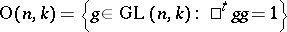 is an analytic subgroup in
is an analytic subgroup in 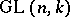 . All closed subgroups of a real or
. All closed subgroups of a real or 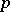 -adic analytic group are analytic, and each continuous homomorphism of such groups is analytic (Cartan's theorems, [1]).
-adic analytic group are analytic, and each continuous homomorphism of such groups is analytic (Cartan's theorems, [1]).
An analytic group is sometimes referred to as a Lie group [1], but a Lie group is usually understood in the narrower sense of a real analytic group [2], [3] (cf. Lie group). Complex and 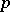 -adic analytic groups are called, respectively, complex and
-adic analytic groups are called, respectively, complex and 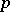 -adic Lie groups.
-adic Lie groups.
The Cartan theorems formulated above signify that the category of real or 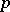 -adic analytic groups is a complete subcategory in the category of locally compact topological groups. The question of the extent to which these categories differ, i.e. as to when a locally compact group
-adic analytic groups is a complete subcategory in the category of locally compact topological groups. The question of the extent to which these categories differ, i.e. as to when a locally compact group 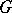 is a real analytic or a
is a real analytic or a 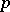 -adic analytic group, can be exhaustively answered: If
-adic analytic group, can be exhaustively answered: If 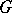 is real analytic, it must contain a neighbourhood of the unit without non-trivial subgroups [5]–[9]; if it is
is real analytic, it must contain a neighbourhood of the unit without non-trivial subgroups [5]–[9]; if it is 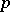 -adic, it must contain a finitely generated open subgroup
-adic, it must contain a finitely generated open subgroup  which is a pro-
which is a pro-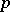 -group and whose commutator subgroup is contained in the set
-group and whose commutator subgroup is contained in the set 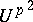 of
of 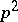 -th powers of elements in
-th powers of elements in 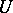 [10]. In particular, any topological group with a neighbourhood of the unit that is homeomorphic to a Euclidean space (a so-called locally Euclidean topological group, [4]) is a real analytic group. In other words, if continuous local coordinates exist in a topological group, it follows that analytic local coordinates exist; this result is the positive solution of Hilbert's fifth problem [5], [11].
[10]. In particular, any topological group with a neighbourhood of the unit that is homeomorphic to a Euclidean space (a so-called locally Euclidean topological group, [4]) is a real analytic group. In other words, if continuous local coordinates exist in a topological group, it follows that analytic local coordinates exist; this result is the positive solution of Hilbert's fifth problem [5], [11].
If the characteristic of the field 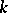 is zero, the most important method in the study of analytic groups is the study of their Lie algebras (cf. Lie algebra of an analytic group).
is zero, the most important method in the study of analytic groups is the study of their Lie algebras (cf. Lie algebra of an analytic group).
For infinite-dimensional analytic groups cf. Lie group, Banach.
References
| [1] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [2] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [3] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
| [4] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
| [5] | "Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 101–115 (Translated from German) |
| [6] | A.M. Gleason, "Groups without small subgroups" Ann. of Math. (2) , 56 : 2 (1952) pp. 193–212 |
| [7] | D. Montgomery, L. Zippin, "Small subgroups for finite dimensional groups" Ann. of Math. (2) , 56 : 2 (1952) pp. 213–241 |
| [8] | H. Yamabe, "On the conjecture of Iwasawa and Gleason" Ann. of Math. (2) , 58 : 1 (1953) pp. 48–54 |
| [9] | H. Yamabe, "A generalization of a theorem of Gleason" Ann. of Math. (2) , 58 : 2 (1953) pp. 351–365 |
| [10] | M. Lazard, "Groupes analytiques 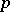 -adiques" Publ. Math. IHES , 26 (1965) -adiques" Publ. Math. IHES , 26 (1965) |
| [11] | I. Kaplansky, "Lie algebras and locally compact groups" , Chicago Univ. Press (1971) |
Comments
In Western literature a connected Lie group is often called an analytic group.
Cartan's theorems usually go back to J. von Neumann (cf. [a1], [a2]).
References
| [a1] | J. von Neumann, , Collected works , 1 , Pergamon (1961) pp. 134–148 |
| [a2] | J. von Neumann, , Collected works , 1 , Pergamon (1961) pp. 509–548 |
Analytic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_group&oldid=12232