Adjunction theory
In its basic form, the study of the interplay between an embedding of a projective manifold (cf. Projective algebraic set)  into projective space and its canonical bundle,
into projective space and its canonical bundle, 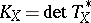 , where
, where  is the cotangent bundle of
is the cotangent bundle of  . For simplicity, below the objects are considered over the complex numbers. The book [a1] is a general reference with full coverage of the literature for the whole theory with its history. The book [a4] is a fine reference on related material.
. For simplicity, below the objects are considered over the complex numbers. The book [a1] is a general reference with full coverage of the literature for the whole theory with its history. The book [a4] is a fine reference on related material.
Classical adjunction theory.
To study a smooth projective algebraic curve  , i.e., a compact Riemann surface, a major approach in the 19th century was to relate properties of the curve to properties of the canonical mapping of the curve, i.e., the mapping of the curve into projective space given by sections of
, i.e., a compact Riemann surface, a major approach in the 19th century was to relate properties of the curve to properties of the canonical mapping of the curve, i.e., the mapping of the curve into projective space given by sections of  . To study a two-dimensional algebraic submanifold of projective space
. To study a two-dimensional algebraic submanifold of projective space  , it was natural to try to reduce questions about the surface
, it was natural to try to reduce questions about the surface 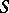 to the hyperplane sections of
to the hyperplane sections of  , i.e., to the curves obtained by slicing
, i.e., to the curves obtained by slicing 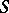 with linear hyperplanes
with linear hyperplanes  . This led to the study of the adjoint bundle
. This led to the study of the adjoint bundle 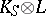 , where
, where 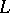 is the restriction to
is the restriction to 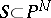 of the hyperplane section bundle of
of the hyperplane section bundle of 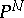 , i.e., the line bundle on
, i.e., the line bundle on 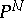 whose sections vanish on hyperplanes of
whose sections vanish on hyperplanes of 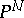 . The restriction of the adjoint bundle to a hyperplane section
. The restriction of the adjoint bundle to a hyperplane section 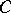 of
of 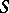 is the canonical bundle of
is the canonical bundle of 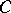 , and, except in a few trivial cases,
, and, except in a few trivial cases, 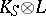 is the only line bundle that has this property. Therefore, if the mapping associated to
is the only line bundle that has this property. Therefore, if the mapping associated to 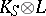 exists, it would tie together the canonical mappings of the smooth hyperplane sections of
exists, it would tie together the canonical mappings of the smooth hyperplane sections of 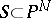 . In the 19th century geometers, especially G. Castelnuovo and F. Enriques, used this rational mapping to study the embedding of
. In the 19th century geometers, especially G. Castelnuovo and F. Enriques, used this rational mapping to study the embedding of 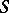 into
into 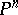 . The general procedure was to consider the sequence
. The general procedure was to consider the sequence 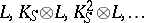 . A classical result was that adjunction terminates, i.e., there is a positive
. A classical result was that adjunction terminates, i.e., there is a positive 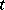 such that
such that 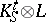 has no sections, if and only if
has no sections, if and only if 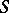 is birational (cf. Birational morphism) to the product of an algebraic curve and
is birational (cf. Birational morphism) to the product of an algebraic curve and 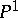 . A key point was that if the above
. A key point was that if the above 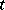 was the first positive
was the first positive  such that
such that 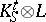 has no sections, then
has no sections, then 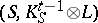 is one of only a "very short list of pairs" . Classically, it was not known if
is one of only a "very short list of pairs" . Classically, it was not known if 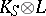 was spanned and, therefore, this procedure did not usually lead to a biregular classification. (A line bundle
was spanned and, therefore, this procedure did not usually lead to a biregular classification. (A line bundle 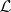 on an algebraic set is said to be spanned if global sections of
on an algebraic set is said to be spanned if global sections of 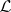 surject onto the fibre of
surject onto the fibre of 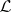 at any point of the algebraic set.) There were also analogous classical procedures on threefolds due to G. Fano and U. Morin (see [a5], [a1]).
at any point of the algebraic set.) There were also analogous classical procedures on threefolds due to G. Fano and U. Morin (see [a5], [a1]).
A.J. Sommese [a6] started the modern study of the mapping (which he called the adjunction mapping) associated to 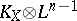 , where
, where 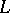 is a very ample line bundle (cf. Ample vector bundle) on an
is a very ample line bundle (cf. Ample vector bundle) on an  -dimensional projective manifold. The complete story with history of the adjunction mapping can be found in [a1], Chapts. 8–11. The fundamental results of this theory are that except for a few special varieties, the pair
-dimensional projective manifold. The complete story with history of the adjunction mapping can be found in [a1], Chapts. 8–11. The fundamental results of this theory are that except for a few special varieties, the pair 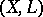 can be replaced by a closely related pair
can be replaced by a closely related pair 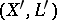 with
with 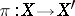 the blow-up of an
the blow-up of an  -dimensional projective manifold
-dimensional projective manifold 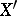 at a finite set,
at a finite set, 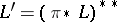 an ample line bundle,
an ample line bundle, 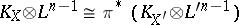 , and
, and 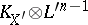 very ample. Moreover, if
very ample. Moreover, if 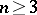 then, except for a few more examples,
then, except for a few more examples, 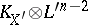 is numerically effective, or nef, i.e.,
is numerically effective, or nef, i.e., 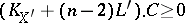 for any effective curve
for any effective curve 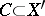 . These results allow the classical birational results alluded to above to be both considerably extended and redone biregularly.
. These results allow the classical birational results alluded to above to be both considerably extended and redone biregularly.
The major open question for this part of adjunction theory is to what extent the mapping associated to 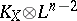 is well-behaved when
is well-behaved when 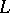 is very ample,
is very ample, 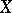 is smooth, and
is smooth, and 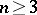 . For example, it is known when
. For example, it is known when  that, except for obvious counterexamples,
that, except for obvious counterexamples, 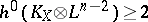 , and if the Kodaira dimension of
, and if the Kodaira dimension of 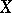 is non-negative, then
is non-negative, then 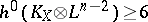 unless
unless 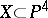 is a quintic threefold with
is a quintic threefold with 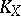 trivial. See [a2], [a1] for this and some further discussion of this problem.
trivial. See [a2], [a1] for this and some further discussion of this problem.
General adjunction theory.
A more abstract approach to adjunction theory is to start with a pair 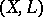 with
with 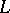 an ample line bundle on a projective variety
an ample line bundle on a projective variety 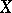 having at worst mild singularities, e.g., terminal singularities. Then, assuming
having at worst mild singularities, e.g., terminal singularities. Then, assuming 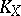 is not nef, Kawamata's theorem asserts that there is a rational number
is not nef, Kawamata's theorem asserts that there is a rational number 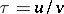 with
with 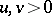 , called the nefvalue of the pair such that
, called the nefvalue of the pair such that  is nef but not ample. By the Kawamata–Shokurov theorem,
is nef but not ample. By the Kawamata–Shokurov theorem, 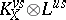 is spanned for all sufficiently large positive integers
is spanned for all sufficiently large positive integers  . The morphism
. The morphism 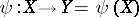 , from
, from 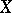 to a normal projective variety
to a normal projective variety 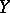 , associated to
, associated to 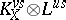 , is independent of
, is independent of  for all sufficiently large
for all sufficiently large  . This mapping
. This mapping 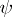 , called the nefvalue morphism of the pair, has connected fibres, and at least one positive-dimensional fibre. If
, called the nefvalue morphism of the pair, has connected fibres, and at least one positive-dimensional fibre. If 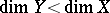 , one can express
, one can express 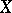 as a very special fibration of Fano varieties, e.g., if
as a very special fibration of Fano varieties, e.g., if 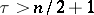 , then
, then 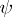 is a contraction of an extremal ray (see [a3] and [a1], Chapt. 6). If
is a contraction of an extremal ray (see [a3] and [a1], Chapt. 6). If 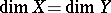 , then one can replace
, then one can replace 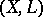 with
with 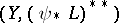 and repeat the procedure. This works well for
and repeat the procedure. This works well for 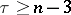 (see [a1], Chapts. 6, 7).
(see [a1], Chapts. 6, 7).
Define the spectral value 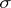 of the pair
of the pair 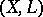 as the infimum of the positive rational numbers
as the infimum of the positive rational numbers  with
with 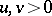 such that there is some positive integer
such that there is some positive integer 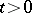 with
with 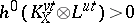 . A major conjecture in this part of the theory is that if
. A major conjecture in this part of the theory is that if 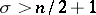 , then
, then 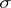 is the nefvalue of the pair
is the nefvalue of the pair 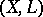 and the nefvalue morphism has a lower-dimensional image.
and the nefvalue morphism has a lower-dimensional image.
References
| [a1] | M.C. Beltrametti, A.J. Sommese, "The adjunction theory of complex projective varieties" , Expositions in Mathematics , 16 , De Gruyter (1995) |
| [a2] | M.C. Beltrametti, A.J. Sommese, "On the dimension of the adjoint linear system for threefolds" Ann. Scuola Norm. Sup. Pisa Cl. Sci. Ser. (4) , XXII (1995) pp. 1–24 |
| [a3] | M.C. Beltrametti, A.J. Sommese, J.A. Wiśniewski, "Results on varieties with many lines and their applications to adjunction theory (with an appendix by M.C. Beltrametti and A.J. Sommese)" K. Hulek (ed.) T. Peternell (ed.) M. Schneider (ed.) F.-O. Schreyer (ed.) , Complex Algebraic Varieties, Bayreuth 1990 , Lecture Notes in Mathematics , 1507 , Springer (1992) pp. 16–38 |
| [a4] | T. Fujita, "Classification theories of polarized varieties" , London Math. Soc. Lecture Notes , 155 , Cambridge Univ. Press (1990) |
| [a5] | L. Roth, "Algebraic threefolds with special regard to problems of rationality" , Springer (1955) |
| [a6] | A.J. Sommese, "Hyperplane sections of projective surfaces, I: The adjunction mapping" Duke Math. J. , 46 (1979) pp. 377–401 |
Adjunction theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjunction_theory&oldid=11576