Lindelöf construction

A geometrical construction to find conjugate points in the problem of finding a minimal surface of revolution (see Fig.).

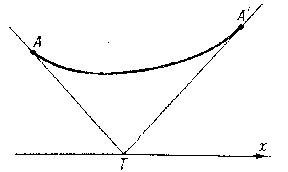
Figure: l058950a

Lindelöf's construction remains suitable for any variational problem of the simplest type on the $(x,y)$-plane for which the general integral of the Euler equation can be represented in the form

$$\frac{y}{c_1}=f\left(\frac{x-c_2}{c_1}\right).$$

The tangents to the extremals at conjugate points $A$ and $A'$ intersect at some point $T$ on the $x$-axis, and the value of the variable integral along the arc $AA'$ is equal to its value on the polygonal line $ATA'$ (see [2]). An example is the catenoid with generating curve

$$\frac{y}{c_1}=\cosh\frac{x-c_2}{c_1}.$$

References

[1]	E. Lindelöf, "Leçons de calcul des variations" , Paris (1861)
[2]	O. Bolza, Bull. Math. Soc. , 18 : 3 (1911) pp. 107–110
[3]	C. Carathéodory, "Variationsrechnung und partielle Differentialgleichungen erster Ordnung" , Teubner (1956)
[a1]	A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Blaisdell (1969)

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️