Lindelöf construction
A geometrical construction to find conjugate points in the problem of finding a minimal surface of revolution (see Fig.).
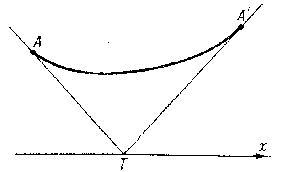
Figure: l058950a
Lindelöf's construction remains suitable for any variational problem of the simplest type on the $(x,y)$-plane for which the general integral of the Euler equation can be represented in the form
$$\frac{y}{c_1}=f\left(\frac{x-c_2}{c_1}\right).$$
The tangents to the extremals at conjugate points $A$ and $A'$ intersect at some point $T$ on the $x$-axis, and the value of the variable integral along the arc $AA'$ is equal to its value on the polygonal line $ATA'$ (see [2]). An example is the catenoid with generating curve
$$\frac{y}{c_1}=\cosh\frac{x-c_2}{c_1}.$$
References
| [1] | E. Lindelöf, "Leçons de calcul des variations" , Paris (1861) |
| [2] | O. Bolza, Bull. Math. Soc. , 18 : 3 (1911) pp. 107–110 |
| [3] | C. Carathéodory, "Variationsrechnung und partielle Differentialgleichungen erster Ordnung" , Teubner (1956) |
| [a1] | A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Blaisdell (1969) |
Lindelöf construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_construction&oldid=53492