Recurrent point

of a dynamical system

A point $ x $ of a dynamical system $ f ^ { t } $( also denoted by $ f( t, \cdot ) $, see [2]) in a metric space $ S $ that satisfies the following condition: For any $ \epsilon > 0 $ there exists a $ T > 0 $ such that all points of the trajectory $ f ^ { t } x $ are contained in an $ \epsilon $- neighbourhood of any arc of time length $ T $ of this trajectory (in other words, with any $ \tau \in \mathbf R $, the $ \epsilon $- neighbourhood of the set

$$ \{ {f ^ { t } x } : {t \in [ \tau , \tau + T ] } \} $$

contains all of the trajectory $ f ^ { t } x $). In this case $ f ^ { t } x $ is called a recurrent trajectory.

Birkhoff's theorem: If the space $ S $ is complete (e.g. $ S = \mathbf R ^ {n} $), then: 1) for a point to be recurrent it is necessary and sufficient that the closure of its trajectory be a compact minimal set; and 2) for the existence of a recurrent point it is sufficient that there be a point that is stable according to Lagrange (see Lagrange stability).

A recurrent point is stable according to Poisson (see Poisson stability), and if the space $ S $ is complete, also stable according to Lagrange (see Lagrange stability). An almost-periodic (in particular, a fixed or periodic) point of a dynamical system is recurrent. In general, any point of a strictly ergodic dynamical system (in a complete space) is recurrent, but the restriction of a dynamical system to the closure of a recurrent trajectory (a minimal set) need not be a strictly ergodic dynamical system (Markov's example, see [2]).

References

[1]	G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927)
[2]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)

Comments

An almost-periodic point of a dynamical system $ f ^ { t } $ on a metric space $ ( S , \rho ) $ is a point $ x \in G $ with the following property: For every $ \epsilon > 0 $ the set

$$ AP ( x, \epsilon ) = \{ {t \in \mathbf R } : { \rho ( f ^ { s+ t } ( x), f ^ { s } ( x) ) < \epsilon \ \textrm{ for all } s \in \mathbf R } \} $$

is relatively dense in $ \mathbf R $, i.e., there exists a length $ l ( \epsilon ) $ such that every interval in $ \mathbf R $ with length $ h \geq l ( \epsilon ) $ contains a point of $ AP( x, \epsilon ) $. (Thus, one might say that the function $ t \mapsto f ^ { t } ( x) : \mathbf R \rightarrow S $ is almost-periodic; cf. Almost-period.)

Another important notion is that of an almost-recurrent point: A point $ x \in S $ such that for every $ \epsilon > 0 $ the set

$$ R( x , U _ \epsilon ) = \ \{ {t \in \mathbf R } : {f ^ { t } ( x) \in U _ \epsilon } \} $$

is relatively dense in $ \mathbf R $, where $ U _ \epsilon $ is the open $ \epsilon $- ball around $ x $. (This definition can easily be generalized to the case of a flow or a cascade on an arbitrary topological space.) The relationship of these notions with that of a recurrent point, Birkhoff's theorem and a number of other implications can be visualized as follows:

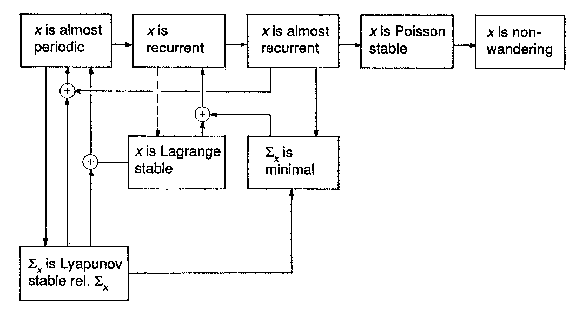
Figure: r080190a

Here the implication indicated by the dotted arrow holds only in a complete space, and $ \Sigma _ {x} $ denotes the closure of the trajectory of $ x $. The property "Sx is Lyapunov stable rel(ative) Sx" means that the family $ \{ f ^ { t } \mid _ {\Sigma _ {x} } \} _ {t \in \mathbf R } $ of functions from $ \Sigma _ {x} $ into $ \Sigma _ {x} $ is equicontinuous on $ \Sigma _ {x} $( see Lyapunov stability). For a refinement of this diagram (including the notions of a pseudo-recurrent point and a uniformly Poisson-stable trajectory) see [a3].

In the literature on topological dynamics (in particular, in the literature directly or indirectly influenced by [a2]) another terminology is in use:

<tbody> </tbody> Above, [2], [a3] [a2] [a1] almost periodic — — recurrent — — almost recurrent almost periodic uniformly recurrent Poisson-stable recurrent recurrent (non-) wandering (not) regionally recurrent —

(To be precise, in [a1] "recurrent" means positive Poisson stable, i.e., $ x $ belongs only to the $ \omega $- limit set of its own trajectory.)

References

[a1]	H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981) Zbl 0459.28023
[a2]	W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955)
[a3]	K.S. [K.S. Sibirskii] Sibirsky, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian)