Vertex operator algebra

Vertex (operator) algebras are a fundamental class of algebraic structures that arose in mathematics and physics in the 1980s. These algebras and their representations are deeply related to many directions in mathematics and physics, in particular, the representation theory of the Fischer–Griess Monster simple finite group and the connection with the phenomena of "Monstrous Moonshine" (cf. also Moonshine conjectures), the representation theory of the Virasoro algebra and affine Kac–Moody Lie algebras (cf. also Kac–Moody algebra), modular functions (cf. also Modular function), the theory of Riemann surfaces (cf. also Riemann surface), knot invariants and invariants of three-manifolds (cf. also Knot theory; Three-dimensional manifold), quantum groups, monodromy associated with differential equations, and conformal and topological field theory and string theory in physics. In fact, the theory of vertex operator algebras and their representations can be thought of as an algebraic foundation of a great number of constructions in these theories. Various equivalent definitions of the notion of vertex algebra and of the variant notion of vertex operator algebra are given below.

The notion of vertex algebra was defined by R. Borcherds [a1] and is a mathematically precise algebraic counterpart of the concept of "chiral algebra" in two-dimensional conformal quantum field theory (a physical theory foundational in string theory [a9] and in two-dimensional statistical mechanics), as formalized by A. Belavin, A.M. Polyakov and A. Zamolodchikov [a3]. This fundamental notion reflects deep features of the traditional notions of commutative associative algebra and at the same time of Lie algebra. The theory of vertex operator algebras has a distinctly non-classical flavour, which can be thought of as analogous to the non-classical flavour of string theory. The elements of a vertex operator algebra correspond to (abstract) "vertex operators" , which in special cases include many of the "vertex operators" introduced by physicists in the early days of string theory to describe hypothesized interactions of certain elementary particles at a "vertex" (cf. also Vertex operator).

One of the main original motivations for the introduction of the notion of vertex (operator) algebra arose from the problem of realizing the Monster $\bf M$ as a symmetry group of a certain infinite-dimensional graded vector space with natural additional structure. The additional structure can be expressed in terms of the axioms defining these new algebraic objects (which are not algebras, not even non-associative algebras, in the usual sense). This problem arose in the study of the remarkable subject of Monstrous Moonshine. In 1978–1979, J. McKay, J.G. Thompson, J.H. Conway and S.P. Norton [a4] conjectured the existence of a natural infinite-dimensional $\bf Z$-graded representation (call it $V ^ { \natural } = \oplus _ { n \geq - 1} V _ { n } ^ { \natural }$) of the then-conjectured Monster group such that the formal series $\sum _ { n \geq - 1 } ( \operatorname { dim } V _ { n } ^ { \natural } ) q ^ { n }$ would be the modular function $J ( q ) = q ^ { - 1 } + 196884 q + \dots$ and such that the action of every element of the Monster on $V ^ { \natural }$ would give rise to a certain modular function with special properties. After R. Griess [a11] proved the existence of $\bf M$ by constructing it as an automorphism group of a remarkable new algebra of dimension 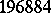, I. Frenkel, J. Lepowsky and A. Meurman [a7] gave a construction, incorporating a vertex operator realization of the Griess algebra, of what they called a "moonshine module" $V ^ { \natural }$ for $\bf M$ having the desired relation with $J ( q )$, and they showed that the action on $V ^ { \natural }$ of certain elements of $\bf M$ gave rise to modular functions. This structure $V ^ { \natural }$ was interpreted by physicists as a "toy model" physical theory of a $26$-dimensional string compactified on a $24$-dimensional "orbifold" associated with the Leech lattice, so that $\bf M$ turned out to be the symmetry group of an idealized physical theory.

Then Borcherds introduced the axiomatic notion of vertex algebra [a1] and perceived that $V ^ { \natural }$ could be endowed with an $\bf M$-invariant vertex algebra structure. An $\bf M$-invariant vertex operator algebra structure on $V ^ { \natural }$ was indeed constructed in [a8]. The Monster is in fact the full symmetry group of this special vertex operator algebra $V ^ { \natural }$, just as the Mathieu finite group $M _ { 24 }$ (cf. also Mathieu group) is the symmetry group of a special error-correcting code, the Golay code, and the Conway finite group $.0$ is the symmetry group of a special positive definite even lattice, the Leech lattice. All three of these special objects possess and can be characterized by the following properties (the uniqueness being conjectural in the case of $V ^ { \natural }$):

a) "self-dual" ,

b) "rank 24" ,

c) "having no small elements" . These properties have appropriate definitions for each of the three types of mathematical structures. In fact, these structures and analogies enter into the construction of $V ^ { \natural }$ ([a7], [a8]). Using the vertex operator algebra structure on $V ^ { \natural }$ and other ideas and results, Borcherds completed in [a2] the proof of the Conway–Norton Monstrous Moonshine conjecture (cf. also Moonshine conjectures) concerning the modular functions associated to elements of $\bf M$, acting on $V ^ { \natural }$.

The notion of vertex operator algebra ([a8], [a6]) is a modification of the notion of vertex algebra. There are several equivalent formulations of these notions, including formulations in terms of "minimal" and "maximal" axioms. The canonical "maximal" axiom is a formal-variable identity called the "Jacobi identity" or the "Jacobi–Cauchy identity" ([a8], [a6]), on which the fundamental principles are heavily based. This identity contains the "full" necessary information in compact form; it is analogous to the classical Jacobi identity in the definition of the notion of Lie algebra; and it is invariant in a natural sense under the symmetric group on three letters. The Jacobi identity and the underlying formal-variable calculus are discussed in detail in [a8] and [a6]. The definition of vertex algebra in [a1] involved certain special cases of the Jacobi identity (see below).

There are also "minimal" axioms, stemming from the fact that the (suitably formulated) "commutativity" of vertex operators implies "associativity" (again suitably formulated) and hence the Jacobi identity, as explained in [a8], [a6] (cf. [a3], [a10]). The simplest "minimal" axiom in the definition of the notion of vertex algebra (see v) below) was found in [a5]. A general and systematic approach and solution to the problem of efficiently constructing examples of vertex operator algebras and their modules, and related problems, was first carried out in [a15].

A program to construct (geometric) conformal field theory using vertex operator algebras and the "sewing" of Riemann spheres with punctures was initiated by Frenkel. A precise geometric formulation of the notion of vertex operator algebra in terms of partial operads of complex powers of the determinant line bundle over the moduli space of Riemann spheres with punctures and local coordinates was given in [a12], [a14], [a13].

Complete definitions of the notions of vertex algebra and vertex operator algebra, using commuting formal variables $x,x_0$, $x_{1} $ and $x _ { 2 }$ are given below. The definition of vertex algebra with either "minimal" or "maximal" axioms is equivalent to Borcherds' definition in [a1]; see below.

Vertex algebras.

A vertex algebra is a vector space $V$ (over $\mathbf{C}$, say) equipped with a linear mapping $V \rightarrow ( \text { End } V ) [ [ x , x ^ { - 1 } ] ]$ (the vector space of formal Laurent series in the formal variable $x$ with coefficients in $\operatorname{End} V$), written as $v \mapsto Y ( v , x )$ (the vertex operator corresponding to the element $v$), and a distinguished vector $\mathbf{1} \in V$, satisfying the following conditions for $u , v \in V$:

i) the formal series $Y ( u , x ) v$ involves only finitely many negative powers of $x$;

ii) $Y ( \mathbf{1} , x ) = 1$ (the identity operator on $V$);

iii) $Y ( v , x ) \bf 1$ involves only non-negative powers of $x$ and its constant term is $v$;

iv) $Y ( v , x ) ] = ( d / d x ) Y ( v , x )$, where $D : V \rightarrow V$ is the mapping such that $D v$ is the constant term of $( d / d x ) Y ( v , x ) \bf 1$ for $v \in V$;

v) there exists a non-negative integer $k$ (depending on $u$ and $v$) such that

\begin{equation*} ( x _ { 1 } - x _ { 2 } ) ^ { k } [ Y ( u , x _ { 1 } ) , Y ( v , x _ { 2 } ) ] = 0. \end{equation*}

In this definition, conditions i–v) are often called the truncation condition, the vacuum property, the creation property, the $D$-bracket-derivative formula, and weak commutativity, respectively. The last condition was formulated and exploited in [a5].

The "main property" of a vertex algebra, the Jacobi identity, states:

vi) For $u , v \in V$,

\begin{equation*} x _ { 0 } ^ { - 1 } \delta \left( \frac { x _ { 1 } - x _ { 2 } } { x _ { 0 } } \right) Y ( u , x _ { 1 } ) Y ( v , x _ { 2 } ) + \end{equation*}

\begin{equation*} - x _ { 0 } ^ { - 1 } \delta ( \frac { x _ { 2 } - x _ { 1 } } { - x _ { 0 } } ) Y ( v , x _ { 2 } ) Y ( u , x _ { 1 } ) = \end{equation*}

\begin{equation*} = x _ { 2 } ^ { - 1 } \delta \left( \frac { x _ { 1 } - x _ { 0 } } { x _ { 2 } } \right) Y ( Y ( u , x _ { 0 } ) v , x _ { 2 } ), \end{equation*}

where $\delta ( x )$ is the formal Laurent series $\sum _ { n \in \bf Z } x ^ { n }$ and, more precisely,

\begin{equation*} x _ { 0 } ^ { - 1 } \delta \left( \frac { x _ { 1 } - x _ { 2 } } { x _ { 0 } } \right) = \sum _ { n \in \mathbf Z } \frac { ( x _ { 1 } - x _ { 2 } ) ^ { n } } { x _ { 0 } ^ { n + 1 } } = \end{equation*}

\begin{equation*} = \sum _ { n \in \mathbf{Z} } \sum _ { k \geq 0 } \left( \begin{array} { c } { n } \\ { k } \end{array} \right) ( - 1 ) ^ { k } x _ { 1 } ^ { n - k } x _ { 2 } ^ { k } x _ { 0 } ^ { - n - 1 }, \end{equation*}

and similarly for the other two $\delta$-function expressions. (All the expressions are well defined.) It can be proved that the axioms ii), iv) and v) can be replaced by the Jacobi identity in the definition. This definition in terms of the Jacobi identity is the definition with "maximal" axioms.

The Jacobi identity is actually the generating function of an infinite family of identities. The use of the three formal variables, rather than complex variables (which can also be used, but with changes in the formulas), allows the full symmetry of the Jacobi identity to reveal itself, as explained in [a8] and [a6].

Vertex algebras also satisfy a "commutativity" condition, which asserts, roughly speaking, that for $u , v \in V$,

\begin{equation*} Y ( u , x _ { 1 } ) Y ( v , x _ { 2 } ) \sim Y ( v , x _ { 2 } ) Y ( u , x _ { 1 } ), \end{equation*}

where "~" denotes equality up to a suitable kind of generalized analytic continuation, and also an "associativity" condition,

\begin{equation*} Y ( u , x _ { 1 } ) Y ( v , x _ { 2 } ) \sim Y ( Y ( u , x _ { 1 } - x _ { 2 } ) v , x _ { 2 } ), \end{equation*}

where the right-hand side and the generalized analytic continuation have to be understood suitably, as explained in [a8] and [a6] (cf. [a3], [a10]). The associativity condition corresponds to the "operator product expansion" for holomorphic fields in conformal field theory, together with its "associativity" . As mentioned above, these two conditions, and even the commutativity condition alone, essentially imply the Jacobi identity. Commutativity and associativity are intimately related to the geometric interpretation of the notion of vertex operator algebra.

Vertex operator algebras.

A vertex operator algebra is a vertex algebra $V$ equipped with a $\bf Z$-grading $V = \oplus _ { n \in \mathbf{Z} } V _ { ( n ) }$ and a distinguished vector $\omega \in V$ satisfying the following additional conditions:

vii) $\operatorname {dim} V _ { ( n ) } < \infty$ for $n \in \mathbf{Z}$ and $V_{( n )} = 0$ for $n$ sufficiently small;

viii) for $m , n \in \mathbf{Z}$,

\begin{equation*} [ L ( m ) , L ( n ) ] = \end{equation*}

\begin{equation*} = ( m - n ) L ( m + n ) + \frac { 1 } { 12 } ( m ^ { 3 } - m ) \delta _ { n + m , 0 } c, \end{equation*}

where $L ( n )$, $n \in \mathbf{Z}$, are the operators on $V$ defined by $Y ( \omega , x ) = \sum _ { n \in \mathbf{Z} } L ( n ) x ^ { - n - 2 }$ and where $c \in \mathbf{C}$;

ix) $L ( 0 ) v = n v$ for $n \in \mathbf{Z}$ and $v \in V_{( n )}$;

x) $Y ( L ( - 1 ) v , x ) = ( d / d x ) Y ( v , x )$.

Conditions vii–x) are often called the grading-restriction conditions, the Virasoro algebra relations, the $L ( 0 )$-grading property and the $L ( - 1 )$-derivative property, respectively.

In [a1], Borcherds gave the following definition: A vertex algebra is a vector space $V$ (actually, this definition works over $\bf Z$ or any other commutative ring) equipped with an element $\mathbf{1}$, linear operators $D^{( i )}$ on $V$ for $i \in \mathbf{Z}$ and bilinear operations $( u , v ) \mapsto u _ { n } ( v )$ from $V \times V$ to $V$, for $n \in \mathbf{Z}$, satisfying the following relations a)–e) for $u , v , w \in V$ and $m , n \in \mathbf{Z}$:

a) $u _ { n } ( w ) = 0$ for $n$ sufficiently large (depending on $u$ and $w$);

b) ${\bf 1} _ { n } ( w ) = 0$ if $n \neq - 1$, $w$ if $n = - 1$;

c) $u _ { n } ( \mathbf{1} ) = D ^ { ( - n - 1 ) } ( u )$;

d) $u_n( v ) = \sum _ { i \geq 0 } ( - 1 ) ^ { i + n + 1 } D ^ { ( i ) } ( v _ { n + i } ( u ) )$;

e) $( u _ { m } ( v ) ) _ { n } ( w ) = \sum _ { i \geq 0 } ( - 1 ) ^ { i } \left( \begin{array} { c } { m } \\ { i } \end{array} \right) ( u _ { m - i }( v _ { n + i} ( w ) ) - ( - 1 ) ^ { m } v _ { m + n - i }( u _ { i } ( w ) ) )$.

It can be proved that the other definitions above of the notion of vertex algebra are equivalent to this one, over a field of characteristic $0$. The relation between the vertex operator mapping and the bilinear operations is given by

\begin{equation*} Y ( u , x ) v = \sum _ { n \in \bf Z } ( u _ { n } v ) x ^ { - n - 1 } \end{equation*}

for $u , v \in V$. Equating the coefficient of the formal variable $x _ { 2 } ^ { - 1 }$ on the two sides of the Jacobi identity above recovers e), in generating-function form.

Among the sources of examples of vertex (operator) algebras are conformal field theory and string theory and related mathematical structures: suitable representations of the Virasoro algebra, of Heisenberg Lie algebras (cf. also Commutation and anti-commutation relationships, representation of) and of Kac–Moody algebras, including affine Lie algebras, and analogues, generalizations and modifications of such structures. Vertex algebras are typically infinite-dimensional, although any commutative associative algebra with derivation carries the structure of a vertex algebra [a1].

References

[a1]	R.E. Borcherds, "Vertex algebras, Kac–Moody algebras, and the Monster" Proc. Nat. Acad. Sci. USA , 83 (1986) pp. 3068–3071
[a2]	R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" Invent. Math. , 109 (1992) pp. 405–444
[a3]	A.A. Belavin, A.M. Polyakov, A.B. Zamolodchikov, "Infinite conformal symmetries in two-dimensional quantum field theory" Nucl. Phys. , B241 (1984) pp. 333–380
[a4]	J.H. Conway, S.P. Norton, "Monstrous moonshine" Bull. London Math. Soc. , 11 (1979) pp. 308–339
[a5]	C. Dong, J. Lepowsky, "Generalized vertex algebras and relative vertex operators" , Progress in Math. , 112 , Birkhäuser (1993)
[a6]	I.B. Frenkel, Y.-Z. Huang, J. Lepowsky, "On axiomatic approaches to vertex operator algebras and modules" , Memoirs , 104 , Amer. Math. Soc. (1993) (preprint: 1989)
[a7]	I.B. Frenkel, J. Lepowsky, A. Meurman, "A natural representation of the Fischer–Griess monster with the modular function $J$ as character" Proc. Nat. Acad. Sci. USA , 81 (1984) pp. 3256–3260
[a8]	I.B. Frenkel, J. Lepowsky, A. Meurman, "Vertex operator algebras and the monster" , Pure Appl. Math. , 134 , Acad. Press (1988)
[a9]	M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , Cambridge Univ. Press (1987)
[a10]	P. Goddard, "Meromorphic conformal field theory" V. Kac (ed.) , Infinite Dimensional Lie Algebras and Groups , Adv. Ser. in Math. Phys. , 7 , World Sci. (1989) pp. 556–587
[a11]	R. Griess, "The friendly giant" Invent. Math. , 69 (1982) pp. 1–102
[a12]	Y.-Z. Huang, "Geometric interpretation of vertex operator algebras" Proc. Nat. Acad. Sci. USA , 88 (1991) pp. 9964–9968
[a13]	Y.-Z. Huang, "Two-dimensional conformal geometry and vertex operator algebras" , Progress in Math. , 148 , Birkhäuser (1997)
[a14]	Y.-Z. Huang, J. Lepowsky, "Vertex operator algebras and operads" L. Corwin (ed.) I. Gel'fand (ed.) J. Lepowsky (ed.) , The Gelfand Mathematical Seminar, 1990-1992 , Birkhäuser (1993) pp. 145–161
[a15]	H. Li, "Local systems of vertex operators, vertex superalgebras and modules" J. Pure Appl. Algebra , 109 (1996) pp. 143–195 (preprint: 1993)