Hopf invariant
An invariant of a homotopy class of mappings of topological spaces. It was first defined by H. Hopf ([1], [2]) for mappings of spheres $ f: S ^ {2n - 1 } \rightarrow S ^ {n} $.
Let $ f: S ^ {2n - 1 } \rightarrow S ^ {n} $ be a continuous mapping. By transition, if necessary, to a homotopic mapping, one may assume that this mapping is simplicial with respect to certain triangulations of the spheres $ S ^ {n} $ and $ S ^ {2n - 1 } $. Then the Hopf invariant is defined as the linking coefficient of the $ ( n - 1) $- dimensional disjoint submanifolds $ f ^ { * } ( a) $ and $ f ^ { * } ( b) $ in $ S ^ {2n - 1 } $ for any distinct $ a, b \in S ^ {n} $.
The mapping $ f: S ^ {2n - 1 } \rightarrow S ^ {n} $ determines an element $ [ f] \in \pi _ {2n - 1 } ( S ^ {n} ) $, and the image of the element $ [ f] $ under the homomorphism
$$ \pi _ {2n - 1 } ( S ^ {n} ) = \ \pi _ {2n - 2 } ( \Omega S ^ {n} ) \rightarrow ^ { h } \ H _ {2n - 2 } ( \Omega S ^ {n} ) = \mathbf Z $$
coincides with the Hopf invariant $ H ( f ) $( here $ h $ is the Hurewicz homomorphism) [3].
Suppose now that $ f: S ^ {2n - 1 } \rightarrow S ^ {n} $ is a mapping of class $ C ^ {2} $ and that a form $ \Omega \in \Lambda ^ {n} S ^ {n} $ is a generator of the integral cohomology group $ H ^ {n} ( S ^ {n} , \mathbf Z ) $. For such a form one may take, for example, $ \Omega = ( dV)/( \mathop{\rm vol} S ^ {n} ) $, where $ dV $ is the volume element on $ S ^ {n} $ in some metric (for example, in the metric given by the imbedding $ S ^ {n} \subset \mathbf R ^ {n + 1 } $), and $ \mathop{\rm vol} S ^ {n} $ is the volume of the sphere $ S ^ {n} $. Then the form $ f ^ { * } ( \Omega ) \in \Lambda ^ {n} S ^ {2n - 1 } $ is closed and it is exact because the group $ H ^ {n} ( S ^ {2n - 1 } , \mathbf Z ) $ is trivial. Thus, $ f ^ { * } ( \Omega ) = d \theta $ for some form $ \theta \in \Lambda ^ {n - 1 } S ^ {2n - 1 } $. A formula for the computation of the Hopf invariant is (see [4]):
$$ H ( f ) = \ \int\limits _ {S ^ {2n - 1 } } \theta \wedge d \theta . $$
The definition of the Hopf invariant can be generalized (see [5], [6]) to the case of mappings $ f: S ^ {m} \rightarrow S ^ {n} $ for $ m \leq 4n - 4 $. In this case there is a decomposition
$$ \tag{* } \pi _ {m} ( S ^ {n} \lor S ^ {n} ) = \ \pi _ {m} ( S ^ {n} ) \oplus \pi _ {m} ( S ^ {n} ) \oplus \pi _ {m} ( S ^ {2n - 1 } ) \oplus \mathop{\rm ker} k _ {*} , $$
where
$$ k _ {*} : \pi _ {m + 1 } ( S ^ {n} \times S ^ {n} ,\ S ^ {n} \lor S ^ {n} ) \rightarrow \ \pi _ {m + 1 } ( S ^ {2n} ) $$
is the homomorphism induced by the projection $ k: ( S ^ {n} \times S ^ {n} , S ^ {n} \lor S ^ {n} ) \rightarrow ( S ^ {n} , \mathop{\rm pt} ) $. Let $ g: S ^ {n} \rightarrow S ^ {n} \lor S ^ {n} $ be the mapping given by contracting the equator of the sphere $ S ^ {n} $ to a point. Then the Hopf invariant is defined as the homomorphism
$$ H: \pi _ {m} ( S ^ {n} ) \rightarrow \pi _ {m} ( S ^ {2n - 1 } ) $$
under which $ [ f] \in \pi _ {m} ( S ^ {n} ) $ is transformed to the projection of the element $ [ g \circ f] \in \pi _ {m} ( S ^ {n} \lor S ^ {n} ) $ onto the direct summand $ \pi _ {m} ( S ^ {2n - 1 } ) $ in the decomposition (*). Since $ \pi _ {2n - 1 } ( S ^ {2n - 1 } ) = \mathbf Z $, for $ m = 2n - 1 $ one obtains the usual Hopf invariant. The generalized Hopf invariant is defined as the composite $ H ^ {*} $ of the homomorphisms
$$ \pi _ {m} ( S ^ {n} ) \rightarrow ^ { {g _ *} } \ \pi _ {m} ( S ^ {n} \lor S ^ {n} ) \rightarrow ^ { p } \ $$
$$ \rightarrow ^ { p } \pi _ { m + 1 } ( S ^ {n} \times S ^ {n} , S ^ {n} \lor S ^ {n} ) \rightarrow ^ { {k _ * } } \pi _ {m + 1 } ( S ^ {2n} ), $$
where $ p $ is the projection of the group $ \pi _ {m} ( S ^ {n} \lor S ^ {n} ) $ onto the direct summand $ \pi _ {m + 1 } ( S ^ {n} \times S ^ {n} , S ^ {n} \lor S ^ {n} ) $, and the homomorphisms $ g _ {*} $ and $ k _ {*} $ are described above. For $ m \leq 4n - 4 $ the Hopf–Whitehead invariant $ H $ and the Hopf–Hilton invariant $ H ^ {*} $ are connected by the relation $ H ^ {*} = S \circ H $, where $ S: \pi _ {m} ( S ^ {2n - 1 } ) \rightarrow \pi _ {m + 1 } ( S ^ {2n} ) $ is the suspension homomorphism (see [6]).
Let $ f: S ^ {2n - 1 } \rightarrow S ^ {n} $ be a mapping and let $ C _ {f} $ be its cylinder (cf. Mapping cylinder). Then the cohomology space $ H ^ {*} ( C _ {f} , S ^ {2n - 1 } ) $ has as homogeneous $ \mathbf Z $- basis a pair $ \{ a, b \} $ with $ \mathop{\rm dim} a = n $ and $ \mathop{\rm dim} b = 2n $. Here the relation $ a ^ {2} = H ( f ) b $ holds (see [7]). If $ n $ is odd, then $ H ( f ) = 0 $( because multiplication in cohomology is skew-commutative).
There is (see [8]) a generalization of the Hopf–Steenrod invariant in terms of a generalized cohomology theory (cf. Generalized cohomology theories). Let $ k $ be the semi-exact homotopy functor in the sense of Dold (see [9]), given on the category of finite CW-complexes and taking values in a certain Abelian category $ A $. Then the mapping of complexes $ f: X \rightarrow Y $ determines an element $ f ^ { * } = d ( f ) \in \mathop{\rm Hom} ( k ( Y), k ( X)) $, where $ \mathop{\rm Hom} $ is the set of morphisms in $ A $. The Hopf–Adams invariant $ e ( f ) $ is defined when $ f ^ { * } = 0 $ and $ d ( Sf ) = 0 $, where $ Sf: SX \rightarrow SY $ is the corresponding suspension mapping. In this case the sequence of cofibrations
$$ X \rightarrow ^ { f } \ Y \rightarrow ^ { f } \ Y \cup _ {f} CX \rightarrow ^ { j } \ SX \mathop \rightarrow \limits ^ {-} Sf \ SY $$
corresponds to an exact sequence in $ A $:
$$ 0 \leftarrow k ( X) \leftarrow ^ { {i _ *} } \ k ( Y \cup _ {f} CX) \leftarrow ^ { {j _ *} } \ k ( SX) \leftarrow 0, $$
which determines the Hopf–Adams–Steenrod invariant $ e ( f ) = \mathop{\rm Ext} ^ {1} ( k ( Y), k ( X)) $.
In the case of the functor $ k = H ^ {*} ( - ; \mathbf Z _ {2} ) $ taking values in the category of modules over the Steenrod algebra modulo 2, one obtains the Hopf–Steenrod invariant $ H _ {2} ( f ) \in \mathbf Z $ of a mapping $ f: S ^ {m} \rightarrow S ^ {n} $ for $ m > n $( see [7]). The cohomology space $ H ^ {*} ( C _ {f} , S ^ {m} ; \mathbf Z _ {2} ) $ has as $ \mathbf Z _ {2} $- basis a pair $ \{ a, b \} $ with $ \mathop{\rm dim} a = n $ and $ \mathop{\rm dim} b = m + 1 $, and then
$$ Sq ^ {m - n + 1 } a = \ H _ {2} ( f ) b. $$
The Hopf invariant $ H _ {p} $ modulo $ p $( where $ p $ is a prime number) is defined as the composite of the mappings
$$ \pi _ {2pn} ( S ^ {2n + 1 } ) _ {(} p) \mathop \rightarrow \limits ^ \approx \ \pi _ {2pn - 2 } ( \Omega ^ {2} S ^ {2n + 1 } ) _ {(} p) \rightarrow $$
$$ \rightarrow \ \pi _ {2pn - 2 } ( \Omega ^ {2} S ^ {2n + 1 } , S ^ {2n - 1 } ) _ {(} p) \rightarrow $$
$$ \rightarrow \ H _ {2pn - 2 } ( \Omega ^ {2} S ^ {2n + 1 } , S ^ {2n - 1 } ) _ {(} p) = \mathbf Z /p, $$
where $ ( X, Y) _ {p} $ is the localization by $ p $ of the pair of spaces (see [10]). Let
$$ S: \pi _ {4n - 1 } ( S ^ {2n} ) \rightarrow \ \pi _ {4n} ( S ^ {2n + 1 } ) $$
be the suspension homomorphism. Then $ H _ {2} ( Sf ) = H _ {2} ( f ) $( see [10]). The Hopf invariant $ H ( f ) $ can also be defined in terms of the Stiefel numbers (cf. Stiefel number) (see [11]): If $ M ^ {n - 1 } $ is a closed equipped manifold and if $ M ^ {n - 1 } = \partial V $, then the characteristic Stiefel–Whitney number $ w _ {n} ( \nu ) [ V, M] $ of the normal bundle $ \nu $ is the same as the Hopf invariant $ H _ {2} ( f ) $ of the mapping $ f: S ^ {n + r - 1 } \rightarrow S ^ {r} $ that is a representative of the class of equipped cobordisms of $ M ^ {n - 1 } $.
The Adams–Novikov spectral sequence makes it possible to construct higher Hopf invariants. Namely, one defines inductively the invariants $ q _ {i} : \mathop{\rm ker} q _ {i - 1 } \rightarrow E _ \infty ^ {i,*} $ and $ q _ {0} : \pi _ {*} ^ {S} \rightarrow E _ \infty ^ {0,*} $( see [12]). From the form of the differentials of this spectral sequence it follows that
$$ \mathop{\rm Ext} _ {AU} ^ {i, * } ( \Omega _ {U} , \Omega _ {U} ) \supset \ E _ \infty ^ {i, * } ,\ \ i = 0, 1, 2, 3 $$
(where $ \Omega _ {U} $ is the ring of complex point cobordisms); therefore, for $ i = 0, 1, 2, 3 $, the invariants $ q _ {i} $ lie in $ \mathop{\rm Ext} _ {AU} ^ {i,*} ( \Omega _ {U} , \Omega _ {U} ) $ and are called the Hopf–Novikov invariants. For $ i = 1 $ one obtains the Adams invariant.
The values that a Hopf invariant can take are not arbitrary. For example, for a mapping $ f: S ^ {4n + 1 } \rightarrow S ^ {2n + 1 } $ the Hopf invariant is always 0. The Hopf invariant modulo $ p $, $ H _ {(} p) : \pi _ {2mp} ( S ^ {2m + 1 } ) \rightarrow \mathbf Z _ {p} $, is trivial, except when $ p = 2 $, $ m = 1, 2, 4 $ and $ p > 2 $, $ m = 1 $. On the other hand, for any even number $ k $ there exists a mapping $ f: S ^ {4n - 1 } \rightarrow S ^ {2n} $ with Hopf invariant $ k $( $ n $ is arbitrary). For $ n = 1, 2, 4 $ there exists mappings $ f: S ^ {4n - 1 } \rightarrow S ^ {2n} $ with Hopf invariant 1.
References
| [1] | H. Hopf, "Ueber die Abbildungen der dreidimensionalen Sphäre auf die Kügelfläche" Math. Ann. , 104 (1931) pp. 639–665 |
| [2] | H. Hopf, "Ueber die Abbildungen von Sphären niedriger Dimension" Fund. Math. , 25 (1935) pp. 427–440 |
| [3] | J.-.P. Serre, "Groupes d'homotopie et classes de groupes abéliens" Ann. of Math. , 58 : 2 (1953) pp. 258–294 |
| [4] | J.H.C. Whitehead, "An expression of the Hopf invariant as an integral" Proc. Nat. Acad. Sci. USA , 33 (1937) pp. 117–123 |
| [5] | J.H.C. Whitehead, "A generation of the Hopf invariant" Ann. of Math. (2) , 51 (1950) pp. 192–237 |
| [6] | P. Hilton, "Suspension theorem and generalized Hopf invariant" Proc. London. Math. Soc. (3) , 1 : 3 (1951) pp. 462–493 |
| [7] | N. Steenrod, "Cohomologies invariants of mappings" Ann. of Math. (2) , 50 (1949) pp. 954–988 |
| [8] | J. Adams, "On the groups 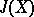 " Topology , 5 (1966) pp. 21–71 " Topology , 5 (1966) pp. 21–71 |
| [9] | A. Dold, "Halbexakte Homotopiefunktoren" , Springer (1966) |
| [10] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [11] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [12] | S.P. Novikov, "The methods of algebraic topology from the view point of cobordism theories" Math. USSR-Izv. , 4 : 1 (1967) pp. 827–913 Izv. AKad. Nauk SSSR Ser. Mat. , 31 : 4 (1967) pp. 855–951 |
| [13] | J.F. Adams, "On the non-existence of elements of Hopf invariant one" Ann. of Math. , 72 (1960) pp. 20–104 |
Hopf invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_invariant&oldid=47270