Martindale ring of quotients
This ring of quotients was introduced in [a6] as a tool to study prime rings satisfying a generalized polynomial identity. Specifically, let 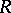 be a prime ring (with
be a prime ring (with 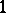 ) and consider all pairs
) and consider all pairs 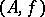 , where
, where 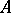 is a non-zero ideal of
is a non-zero ideal of 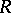 and where
and where 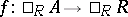 is a left
is a left 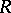 -module mapping. One says that
-module mapping. One says that 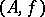 and
and 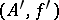 are equivalent if
are equivalent if  and
and 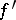 agree on their common domain
agree on their common domain 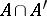 . This is easily seen to yield an equivalence relation, and the set
. This is easily seen to yield an equivalence relation, and the set  of all equivalence classes
of all equivalence classes 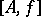 is a ring extension of
is a ring extension of 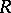 with arithmetic defined by
with arithmetic defined by
 |
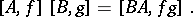 |
Here, 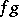 indicates the mapping
indicates the mapping 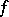 followed by the mapping
followed by the mapping 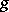 .
.
One can show (see [a12]) that the left Martindale ring of quotients 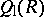 is characterized as the unique (up to isomorphism) ring extension
is characterized as the unique (up to isomorphism) ring extension 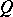 of
of 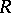 satisfying:
satisfying:
1) if 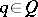 , then there exists a
, then there exists a  with
with 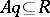 ;
;
2) if 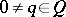 and
and 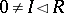 , then
, then 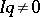 ; and
; and
3) if 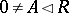 and
and 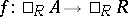 , then there exists a
, then there exists a 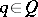 with
with 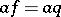 for all
for all 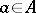 . As a consequence, if
. As a consequence, if 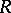 is simple, then
is simple, then 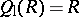 . In any case,
. In any case, 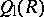 is certainly a prime ring. The right Martindale ring of quotients
is certainly a prime ring. The right Martindale ring of quotients 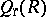 is defined in an analogous manner and enjoys similar properties.
is defined in an analogous manner and enjoys similar properties.
Again, let 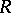 be a prime ring and write
be a prime ring and write 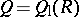 . Then
. Then 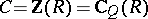 is a field known as the extended centroid of
is a field known as the extended centroid of 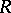 , and the subring
, and the subring 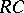 of
of 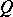 is called the central closure of
is called the central closure of 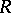 . One can show that
. One can show that 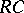 is a prime ring which is centrally closed, namely it contains its extended centroid. This central closure controls the linear identities of
is a prime ring which is centrally closed, namely it contains its extended centroid. This central closure controls the linear identities of 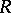 in the sense that if
in the sense that if 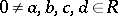 with
with 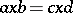 for all
for all 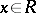 , then there exists an element
, then there exists an element 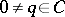 with
with 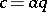 and
and 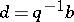 . Martindale's theorem [a6] asserts that a prime ring
. Martindale's theorem [a6] asserts that a prime ring 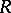 satisfies a non-trivial generalized polynomial identity if and only if
satisfies a non-trivial generalized polynomial identity if and only if 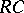 has an idempotent
has an idempotent  such that
such that 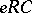 is a minimal right ideal and
is a minimal right ideal and 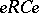 is a division algebra that is finite dimensional over
is a division algebra that is finite dimensional over 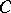 .
.
If 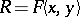 is a non-commutative free algebra in two variables, then
is a non-commutative free algebra in two variables, then 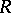 is a domain but
is a domain but 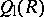 is not. Thus
is not. Thus 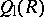 is in some sense too large an extension of
is in some sense too large an extension of 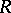 . In [a3], it was suggested that for any prime ring
. In [a3], it was suggested that for any prime ring 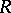 , the set
, the set 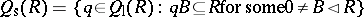 would define a symmetric version of the Martindale ring of quotients. This was shown to be the case in [a12], where
would define a symmetric version of the Martindale ring of quotients. This was shown to be the case in [a12], where 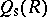 was characterized as the unique (up to isomorphism) ring extension
was characterized as the unique (up to isomorphism) ring extension 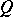 of
of 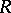 satisfying:
satisfying:
a) if 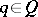 , then there exist
, then there exist 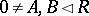 with
with 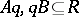 ;
;
b) if 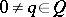 and
and 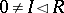 , then
, then 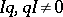 ; and
; and
c) if 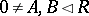 ,
, 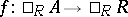 ,
, 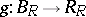 and
and 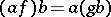 for all
for all 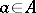 ,
, 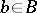 , then there exists a
, then there exists a 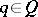 with
with 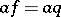 and
and 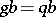 for all
for all  ,
, 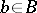 .
.
When 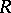 is a domain, then so is its symmetric Martindale ring of quotients
is a domain, then so is its symmetric Martindale ring of quotients 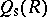 . Furthermore, any non-commutative free algebra is symmetrically closed.
. Furthermore, any non-commutative free algebra is symmetrically closed.
An interesting example here is as follows. Let 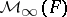 denote the
denote the  -vector space of all square matrices of some infinite size, and let
-vector space of all square matrices of some infinite size, and let 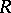 be the subspace which is the direct sum of the scalar matrices and the matrices with only finitely many non-zero entries. Then
be the subspace which is the direct sum of the scalar matrices and the matrices with only finitely many non-zero entries. Then 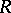 is a prime ring,
is a prime ring, 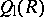 is the ring of row-finite matrices in
is the ring of row-finite matrices in 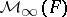 ,
, 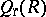 is the ring of column-finite matrices, and
is the ring of column-finite matrices, and 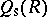 is the ring consisting of matrices which are both row and column finite. Thus, in some rough sense,
is the ring consisting of matrices which are both row and column finite. Thus, in some rough sense, 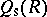 is the intersection of the left and right Martindale rings of quotients. Other examples of interest can be found in [a2], [a4], [a5], [a8], [a13].
is the intersection of the left and right Martindale rings of quotients. Other examples of interest can be found in [a2], [a4], [a5], [a8], [a13].
Another important intermediate ring is the normal closure of 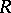 , defined in [a10] as the product
, defined in [a10] as the product  , where
, where 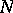 is the multiplicatively closed set of all units
is the multiplicatively closed set of all units 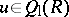 with
with 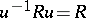 . Then
. Then 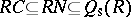 , and
, and 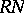 is the smallest ring extension of
is the smallest ring extension of 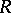 needed to study all group actions on
needed to study all group actions on  . Despite its name, the normal closure is not necessarily normally closed. Again, numerous examples of these normal closures have been computed. See, for example, [a7], [a9], [a11].
. Despite its name, the normal closure is not necessarily normally closed. Again, numerous examples of these normal closures have been computed. See, for example, [a7], [a9], [a11].
Finally, as was pointed out in [a1], there is a more general construction which yields analogues of the Martindale ring of quotients for rings which are not necessarily prime. To this end, let 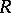 be an arbitrary ring (with
be an arbitrary ring (with 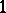 ) and let
) and let 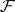 be a non-empty filter of ideals of
be a non-empty filter of ideals of 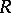 . Specifically, it is assumed that:
. Specifically, it is assumed that:
every ideal 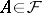 is regular, that is, has trivial right and left annihilator in
is regular, that is, has trivial right and left annihilator in 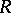 ;
;
if 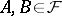 , then
, then 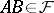 ; and
; and
if 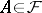 and if
and if 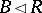 with
with 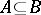 , then
, then 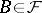 . Given such a filter, one can again consider all pairs
. Given such a filter, one can again consider all pairs 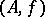 with
with 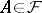 and with
and with 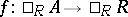 , and use these to construct a ring extension of
, and use these to construct a ring extension of 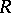 which might be denoted by
which might be denoted by 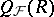 . For example, if
. For example, if 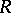 is a semi-prime ring, then the set
is a semi-prime ring, then the set 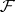 of all regular ideals is such a filter. Here, if
of all regular ideals is such a filter. Here, if 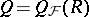 , then the centre
, then the centre 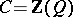 is no longer a field, in general, but it is at least a commutative regular ring (in the sense of von Neumann). Another example of interest occurs when
is no longer a field, in general, but it is at least a commutative regular ring (in the sense of von Neumann). Another example of interest occurs when 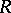 is a
is a 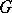 -prime ring, where
-prime ring, where 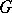 is a fixed group of automorphisms of
is a fixed group of automorphisms of 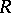 . In this case, one can take
. In this case, one can take 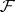 to be the set of non-zero
to be the set of non-zero 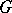 -stable ideals of
-stable ideals of 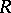 , and then the action of
, and then the action of 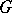 on
on 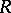 extends to an action on
extends to an action on  .
.
References
| [a1] | S.A. Amitsur, "On rings of quotients" , Symposia Math. , VIII , Acad. Press (1972) pp. 149–164 |
| [a2] | P. Ara, A. del Rio, "A question of Passman on the symmetric ring of quotients" Israel J. Math. , 68 (1989) pp. 348–352 |
| [a3] | V.K. Kharchenko, "Generalized identities with automorphisms" Algebra and Logic , 14 (1976) pp. 132–148 Algebra i Logika , 14 (1975) pp. 215–237 |
| [a4] | V.K. Kharchenko, "Algebras of invariants of free algebras" Algebra and Logic , 17 (1979) pp. 316–321 Algebra i Logika , 17 (1978) pp. 478–487 |
| [a5] | J. Lewin, "The symmetric ring of quotients of a  -fir" Commun. Algebra , 16 (1988) pp. 1727–1732 -fir" Commun. Algebra , 16 (1988) pp. 1727–1732 |
| [a6] | W.S. Martindale III, "Prime rings satisfying a generalized polynomial identity" J. Algebra , 12 (1969) pp. 576–584 |
| [a7] | W.S. Martindale III, "The normal closure of the coproduct of rings over a division ring" Trans. Amer. Math. Soc. , 293 (1986) pp. 303–317 |
| [a8] | W.S. Martindale III, "The symmetric ring of quotients of the coproduct of rings" J. Algebra , 143 (1991) pp. 295–306 |
| [a9] | W.S. Martindale III, S. Montgomery, "The normal closure of coproducts of domains" J. Algebra , 82 (1983) pp. 1–17 |
| [a10] | S. Montgomery, "Automorphism groups of rings with no nilpotent elements" J. Algebra , 60 (1979) pp. 238–248 |
| [a11] | S. Montgomery, "X-inner automorphisms of filtered algebras" Proc. Amer. Math. Soc. , 83 (1981) pp. 263–268 |
| [a12] | D.S. Passman, "Computing the symmetric ring of quotients" J. Algebra , 105 (1987) pp. 207–235 |
| [a13] | J.D. Rosen, M.P. Rosen, "The Martindale ring of quotients of a skew polynomial ring of automorphism type" Commun. Algebra , 21 (1993) pp. 4051–4063 |
Martindale ring of quotients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Martindale_ring_of_quotients&oldid=39309