D0L-sequence

$L$-systems were introduced by A. Lindenmayer in the late 1960s to model (in discrete time) the development of filamentous organisms. A fundamental feature of these systems is that in each step each cell (represented by a symbol from a finite alphabet) has to be rewritten according to the developmental rules of the organism. This parallelism is the main difference between $L$-systems and the classical Chomsky grammars (cf. also Grammar, generative). In fact, soon after their introduction, $L$-systems constituted a significant part of formal language theory, allowing one to compare parallel rewriting to a more classical sequential one, see [a13].

The simplest $L$-system is a so-called D$0$L-system, where the development starts from a single word and continues deterministically step by step in a context independent way, that is, the development of a symbol depends only on that symbol. (Here, "D" stands for determinism, $0$ for zero-sided interaction and "L" for Lindenmayer.) Formally, a D$0$L-system is a triple $\mathcal{G} = (\Sigma,h,w)$, where $\Sigma$ is a finite alphabet, $h$ is an endomorphism of the free monoid generated by $\Sigma$, in symbols $\Sigma^*$, and $w$ is a starting word. The system $\mathcal{G}$ defines the D$0$L-sequence $$S(\mathcal{G})\ : \ w,\,h(w),\,h^2(w),\,\ldots$$ the D$0$L-growth sequence $$GS(\mathcal{G})\ : \ |w|,\,|h(w)|,\,|h^2(w)|,\,\ldots$$ where $| \cdot |$ denotes the length of a word, and the D$0$L-language $$L(\mathcal{G}) = \{ h^i(w) : i \ge 0 \} \ .$$

It is not only the mathematical simplicity of the definitions, but rather the challenging mathematical problems connected with these notions, in particular with D$0$L-sequences, which made D$0$L-systems mathematically very fruitful. The most famous problem is the D$0$L-sequence equivalence problem, which asks for an algorithm to decide whether or not two D$0$L-sequences coincide. The impact of this nice problem is discussed in [a11].

D$0$L-languages emphasize a static nature of the systems and are more related to classical formal language theory. D$0$L-growth sequences, in turn, are closely connected to the theory of $\mathbf{N}$-rational formal power series, and in fact allow one to reformulate certain classical problems, such as the algorithmic problem on the existence of a zero in a sequence defined by a linear recurrence, see [a15]. Finally, D$0$L-sequences represent a dynamical feature of the systems. Moreover, such sequences are defined in a very simple and natural way: by iterating a morphism.

The D$0$L-sequence equivalence problem was first shown to be algorithmically decidable in [a4] (cf. also Proof theory). A simpler solution was found in [a7], and finally a third completely different solution can be based on the validity of the Ehrenfeucht conjecture and Makanin's algorithm for the solvability of word equations over free monoids, as shown in [a6]. It is interesting to note that only the third solution extends to a multi-dimensional variant of the D$0$L-problem, the so-called DT$0$L-sequence equivalence problem. In the latter problem, the word sequences of (a1) are replaced by $k$-ary trees obtained by iterating $k$ different morphisms in all possible ways.

Despite the above solutions, an intriguing feature of the D$0$L-sequence equivalence problem remains. Indeed, none of the above solutions is practical. However, it has been conjectured that only the $2.\mathrm{card}(\Sigma)$ first elements of the sequences have to be compared in order to decide the equivalence. This $2n$-conjecture is known to hold when $\Sigma$ is binary, see [a10], but no reasonable (even exponential) bound is known (1998) in the general case.

As already hinted at, the major mathematical importance of D$0$L-systems lies in the fact that they (in particular, the research on the D$0$L-sequence equivalence problem) motivated a large amount of fundamental research on morphisms of free monoids. Below a few such examples are given.

Consider a morphism $h : \Sigma^* \rightarrow \Sigma^*$ satisfying $h(a) = au$ for some $a \in \Sigma$ and $u \in \Sigma^{+}$. If $h$ is non-erasing, i.e. $h(b) \neq 1$ for all $b \in \Sigma$, then there exists a unique infinite word $$w_h = \lim_{i \rightarrow \infty} h^i(a) \ .$$

Consequently, D$0$L-sequences can be used in a very natural way to define infinite words. Implicitly, A. Thue used this approach at the beginning of the 20th century in his seminal work on square- and cube-free infinite words over a finite alphabet, see [a16]. Since the early 1980s, such a research on non-repetitive words, revitalized by [a2], has been a central topic in the combinatorics of words. Almost exclusively non-repetitive words are constructed by the above method of iterating a morphism.

The D$0$L-sequence equivalence problem asks whether or not two morphisms $f$ and $g$ agree on a D$0$L-language defined by one of the morphisms, that is, whether or not $f(x) = g(x)$ for all $x$ in $\{ h^i(a) : i \ge 0 \}$. This has motivated the consideration of so-called equality languages of two morphisms $f,g : \Sigma^* \rightarrow \Delta^*$: $$E(f,g) = \{ x \in \Sigma^* : f(x) = g(x) \} \ .$$

Research on equality languages revealed amazing morphic characterizations of recursively enumerable languages, see [a3], [a8] and [a14]. For example, each recursively enumerable language (cf. also Formal languages and automata) can be expressed in the form $L = \pi(E(f,g) \cap R)$, where $\pi$, $f$ and $g$ are morphisms and $R$ is a regular language (cf. also Grammar, regular). Furthermore, the fundamental Post correspondence problem can be formulated as a problem of deciding whether or not $E(f,g) = \{1\}$, where $1$ denotes the unit of the free monoid $\Sigma^*$.

A third, and apparently the most fundamental, consequence of research on D$0$L-systems was a discovery of a compactness property of free semi-groups: Each system of equations over a free monoid containing a finite number of variables is equivalent to some of its finite subsystems (cf. also Free semi-group). This property (often referred to as the Ehrenfeucht conjecture) was conjectured by A. Ehrenfeucht in the early 1970s (in a slightly different form) and later established in [a1] and [a9].

Finally, it is worth mentioning that besides their mathematical inspiration, D$0$L-sequences have turned out to be useful in areas such as computer graphics and simulation of biological developments, see [a5] and [a12].

References

[a1]	M. Albert, J. Lawrence, "A proof of Ehrenfeucht's conjecture" Theoret. Comput. Sci. , 41 (1985) pp. 121–123
[a2]	J. Bertel, "Mots sans carré et morphismes itérés" Discrete Math. , 29 (1979) pp. 235–244
[a3]	K. Culik II, "A purely homomorphic characterization of recursively enumerable sets" J. Assoc. Comput. Mach. , 26 (1979) pp. 345–350
[a4]	K. Culik II, I. Fris, "The decidability of the equivalence problem for D0L-systems" Inform. Control , 35 (1977) pp. 20–39
[a5]	K. Culik II, J. Kari, "On the power of 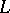-systems in image generation" G. Rozenberg (ed.) A. Salomaa (ed.) , Developments in Language Theory , World Sci. (1994) pp. 225–236
[a6]	K. Culik II, J. Karhumäki, "Systems of equations over a free monoid and Ehrenfeucht's Conjecture" Discrete Math. , 43 (1983) pp. 139–153
[a7]	A. Ehrenfeucht, G. Rozenberg, "Elementary homomorphisms and a solution to D$0$L-sequence equivalence problem" Theoret. Comput. Sci. , 7 (1978) pp. 169–183
[a8]	J. Engelfriet, G. Rozenberg, "Fixed point languages, equality languages, and representation of recursively enumerable languages" J. Assoc. Comput. Mach. , 27 (1980) pp. 499–518
[a9]	V.S. Guba, "The equivalence of infinite systems of equations in free groups and semigroups with finite subsystems" Mat. Zametki , 40 (1986) pp. 321–324 (In Russian)
[a10]	J. Karhumäki, "On the equivalence problem for binary D0L systems" Inform. Control , 50 (1981) pp. 276–284
[a11]	J. Karhumäki, "The impact of the D$0$L-problem" G. Rozenberg (ed.) A. Salomaa (ed.) , Current Trends in Theoretical Computer Science. Essays and Tutorials , World Sci. (1993) pp. 586–594
[a12]	P. Prusinkiewicz, M. Hammel, J. Hanan, R. Měch, "Visual models of plant development" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , III , Springer (1997) pp. 535–597
[a13]	G. Rozenberg, A. Salomaa, "The mathematical theory of $L$-systems" , Acad. Press (1980)
[a14]	A. Salomaa, "Equality sets for homomorphisms of free monoids" Acta Cybernetica , 4 (1978) pp. 127–139
[a15]	A. Salomaa, M. Soittola, "Automata-theoretic aspects of formal power series" , Springer (1978)
[a16]	A. Thue, "Über unendliche Zeichereichen" Kra. Vidensk. Selsk. Skr. I. Mat.-Nat. Kl. , 7 (1906)