D0L-sequence

$L$-systems were introduced by A. Lindenmayer in the late 1960s to model (in discrete time) the development of filamentous organisms. A fundamental feature of these systems is that in each step each cell (represented by a symbol from a finite alphabet) has to be rewritten according to the developmental rules of the organism. This parallelism is the main difference between $L$-systems and the classical Chomsky grammars (cf. also Grammar, generative). In fact, soon after their introduction, $L$-systems constituted a significant part of formal language theory, allowing one to compare parallel rewriting to a more classical sequential one, see [a13].

The simplest $L$-system is a so-called D$0$L-system, where the development starts from a single word and continues deterministically step by step in a context independent way, that is, the development of a symbol depends only on that symbol. (Here, "D" stands for determinism, $0$ for zero-sided interaction and "L" for Lindenmayer.) Formally, a D$0$L-system is a triple $\mathcal{G} = (\Sigma,h,w)$, where $\Sigma$ is a finite alphabet, $h$ is an endomorphism of the free monoid generated by $\Sigma$, in symbols $\Sigma^*$, and $w$ is a starting word. The system $\mathcal{G}$ defines the D$0$L-sequence $$ S(\mathcal{G})\ : \ w,\,h(w),\,h^2(w),\,\ldots $$ the D$0$L-growth sequence $$ GS(\mathcal{G})\ : \ |w|,\,|h(w)|,\,|h^2(w)|,\,\ldots $$ where $| \cdot |$ denotes the length of a word, and the D$0$L-language $$ L(\mathcal{G}) = \{ h^i(w) : i \ge 0 \} \ . $$

It is not only the mathematical simplicity of the definitions, but rather the challenging mathematical problems connected with these notions, in particular with D$0$L-sequences, which made D$0$L-systems mathematically very fruitful. The most famous problem is the D$0$L-sequence equivalence problem, which asks for an algorithm to decide whether or not two D$0$L-sequences coincide. The impact of this nice problem is discussed in [a11].

D$0$L-languages emphasize a static nature of the systems and are more related to classical formal language theory. D$0$L-growth sequences, in turn, are closely connected to the theory of $\mathbf{N}$-rational formal power series, and in fact allow one to reformulate certain classical problems, such as the algorithmic problem on the existence of a zero in a sequence defined by a linear recurrence, see [a15]. Finally, D$0$L-sequences represent a dynamical feature of the systems. Moreover, such sequences are defined in a very simple and natural way: by iterating a morphism.

The D$0$L-sequence equivalence problem was first shown to be algorithmically decidable in [a4] (cf. also Proof theory). A simpler solution was found in [a7], and finally a third completely different solution can be based on the validity of the Ehrenfeucht conjecture and Makanin's algorithm for the solvability of word equations over free monoids, as shown in [a6]. It is interesting to note that only the third solution extends to a multi-dimensional variant of the D$0$L-problem, the so-called DT$0$L-sequence equivalence problem. In the latter problem, the word sequences of (a1) are replaced by $k$-ary trees obtained by iterating $k$ different morphisms in all possible ways.

Despite the above solutions, an intriguing feature of the D$0$L-sequence equivalence problem remains. Indeed, none of the above solutions is practical. However, it has been conjectured that only the 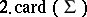first elements of the sequences have to be compared in order to decide the equivalence. This 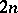-conjecture is known to hold when 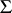is binary, see [a10], but no reasonable (even exponential) bound is known (1998) in the general case.

As already hinted at, the major mathematical importance of D$0$L-systems lies in the fact that they (in particular, the research on the D$0$L-sequence equivalence problem) motivated a large amount of fundamental research on morphisms of free monoids. Below a few such examples are given.

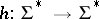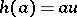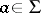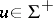Consider a morphism satisfying for some and . If 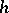is non-erasing, i.e. 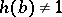for all 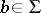, then there exists a unique infinite word

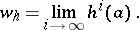Consequently, D$0$L-sequences can be used in a very natural way to define infinite words. Implicitly, A. Thue used this approach at the beginning of the 20th century in his seminal work on square- and cube-free infinite words over a finite alphabet, see [a16]. Since the early 1980s, such a research on non-repetitive words, revitalized by [a2], has been a central topic in the combinatorics of words. Almost exclusively non-repetitive words are constructed by the above method of iterating a morphism.

The D$0$L-sequence equivalence problem asks whether or not two morphism 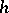and 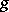agree on a D$0$L-language defined by one of the morphisms, that is, whether or not 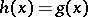for all in 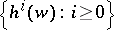. This has motivated the consideration of so-called equality languages of two morphisms :

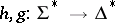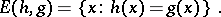Research on equality languages revealed amazing morphic characterizations of recursively enumerable languages, see [a3], [a8] and [a14]. For example, each recursively enumerable language (cf. also Formal languages and automata) can be expressed in the form 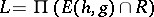, where 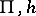and 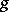are morphisms and 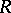is a regular language (cf. also Grammar, regular). Furthermore, the fundamental Post correspondence problem can be formulated as a problem of deciding whether or not 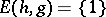, where 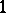denotes the unit of the free monoid .

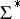A third, and apparently the most fundamental, consequence of research on D$0$L-systems was a discovery of a compactness property of free semi-groups: Each system of equations over a free monoid containing a finite number of variables is equivalent to some of its finite subsystems (cf. also Free semi-group). This property (often referred to as the Ehrenfeucht conjecture) was conjectured by A. Ehrenfeucht in the early 1970s (in a slightly different form) and later established in [a1] and [a9].

Finally, it is worth mentioning that besides their mathematical inspiration, D$0$L-sequences have turned out to be useful in areas such as computer graphics and simulation of biological developments, see [a5] and [a12].

References

[a1]	M. Albert, J. Lawrence, "A proof of Ehrenfeucht's conjecture" Theoret. Comput. Sci. , 41 (1985) pp. 121–123
[a2]	J. Bertel, "Mots sans carré et morphismes itérés" Discrete Math. , 29 (1979) pp. 235–244
[a3]	K. Culik II, "A purely homomorphic characterization of recursively enumerable sets" J. Assoc. Comput. Mach. , 26 (1979) pp. 345–350
[a4]	K. Culik II, I. Fris, "The decidability of the equivalence problem for D0L-systems" Inform. Control , 35 (1977) pp. 20–39
[a5]	K. Culik II, J. Kari, "On the power of 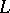-systems in image generation" G. Rozenberg (ed.) A. Salomaa (ed.) , Developments in Language Theory , World Sci. (1994) pp. 225–236
[a6]	K. Culik II, J. Karhumäki, "Systems of equations over a free monoid and Ehrenfeucht's Conjecture" Discrete Math. , 43 (1983) pp. 139–153
[a7]	A. Ehrenfeucht, G. Rozenberg, "Elementary homomorphisms and a solution to D$0$L-sequence equivalence problem" Theoret. Comput. Sci. , 7 (1978) pp. 169–183
[a8]	J. Engelfriet, G. Rozenberg, "Fixed point languages, equality languages, and representation of recursively enumerable languages" J. Assoc. Comput. Mach. , 27 (1980) pp. 499–518
[a9]	V.S. Guba, "The equivalence of infinite systems of equations in free groups and semigroups with finite subsystems" Mat. Zametki , 40 (1986) pp. 321–324 (In Russian)
[a10]	J. Karhumäki, "On the equivalence problem for binary D0L systems" Inform. Control , 50 (1981) pp. 276–284
[a11]	J. Karhumäki, "The impact of the D$0$L-problem" G. Rozenberg (ed.) A. Salomaa (ed.) , Current Trends in Theoretical Computer Science. Essays and Tutorials , World Sci. (1993) pp. 586–594
[a12]	P. Prusinkiewicz, M. Hammel, J. Hanan, R. Měch, "Visual models of plant development" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , III , Springer (1997) pp. 535–597
[a13]	G. Rozenberg, A. Salomaa, "The mathematical theory of $L$-systems" , Acad. Press (1980)
[a14]	A. Salomaa, "Equality sets for homomorphisms of free monoids" Acta Cybernetica , 4 (1978) pp. 127–139
[a15]	A. Salomaa, M. Soittola, "Automata-theoretic aspects of formal power series" , Springer (1978)
[a16]	A. Thue, "Über unendliche Zeichereichen" Kra. Vidensk. Selsk. Skr. I. Mat.-Nat. Kl. , 7 (1906)