Howell design
A Howell design of side  and order
and order  , or more briefly an
, or more briefly an 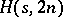 , is an
, is an 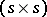 -array in which each cell is either empty or contains an unordered pair of distinct elements from some
-array in which each cell is either empty or contains an unordered pair of distinct elements from some 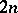 -set
-set 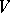 such that:
such that:
1) every element of 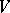 occurs in precisely one cell of each row and each column;
occurs in precisely one cell of each row and each column;
2) every unordered pair of elements from 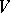 is in at most one cell of the array. It follows immediately from the definition of an
is in at most one cell of the array. It follows immediately from the definition of an 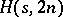 that
that 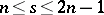 . An example of a Howell design is the following
. An example of a Howell design is the following 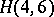 :
:
<tbody> </tbody>
|
An 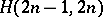 is also called a Room square of side
is also called a Room square of side 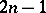 . At the other extreme, the existence of a pair of mutually orthogonal Latin squares implies the existence of an
. At the other extreme, the existence of a pair of mutually orthogonal Latin squares implies the existence of an  . The existence of Howell designs has been completely determined [a1], [a5]: Let
. The existence of Howell designs has been completely determined [a1], [a5]: Let  and
and  be positive integers such that
be positive integers such that 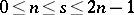 . There exists an
. There exists an 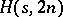 if and only if
if and only if 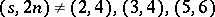 or
or  . The proof uses a variety of direct and recursive constructions.
. The proof uses a variety of direct and recursive constructions.
An 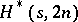 is an
is an 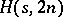 in which there is a subset
in which there is a subset 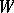 of
of 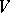 ,
, 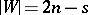 , such that no pair of elements from
, such that no pair of elements from  appears in the design.
appears in the design.  -designs are quite useful in recursive constructions. There exist
-designs are quite useful in recursive constructions. There exist 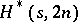 for
for  even,
even, 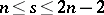 , with two exceptions: there is no
, with two exceptions: there is no 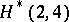 and there is no
and there is no 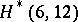 [a1]. The existence of
[a1]. The existence of 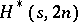 for
for  odd remains open, see [a5]. The only known case where an
odd remains open, see [a5]. The only known case where an 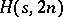 exists but an
exists but an 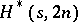 does not is for
does not is for 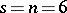 .
.
The pairs of elements in the cells of an 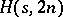 can be thought of as the edges of an
can be thought of as the edges of an  -regular graph on the
-regular graph on the 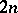 -set
-set 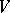 , the underlying graph of the Howell design. The existence of an
, the underlying graph of the Howell design. The existence of an 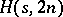 is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the
is equivalent to the existence of a pair of orthogonal one-factorizations of the underlying graph of the 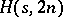 (cf. One-factorization). The underlying graph of an
(cf. One-factorization). The underlying graph of an 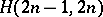 is the complete graph
is the complete graph 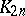 , and the underlying graph of an
, and the underlying graph of an 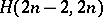 is the cocktail party graph
is the cocktail party graph 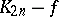 , where
, where 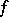 is a one-factor. An
is a one-factor. An 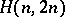 with underlying graph
with underlying graph 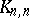 is equivalent to a pair of mutually orthogonal Latin squares of order
is equivalent to a pair of mutually orthogonal Latin squares of order  . The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [a3].
. The general problem of determining which graphs are the underlying graphs of a Howell design remains open (1996), see [a3].
Several special types of Howell designs have been studied, including  -designs, skew designs, complementary designs,
-designs, skew designs, complementary designs,  -complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [a3] [a4]).
-complementary designs, cyclic Howell designs (used for Howell movements in duplicate bridge), and Howell designs with Howell sub-designs (see [a3] [a4]).
A 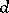 -dimensional Howell design,
-dimensional Howell design, 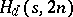 , is a
, is a 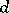 -dimensional array in which every cell either is empty or contains an unordered pair of elements from a
-dimensional array in which every cell either is empty or contains an unordered pair of elements from a 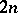 -set
-set 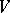 and such that each two-dimensional projection is an
and such that each two-dimensional projection is an 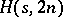 . An
. An  is called a Howell cube. An
is called a Howell cube. An 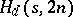 is equivalent to
is equivalent to 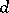 mutually orthogonal one-factorizations of the underlying graph. Let
mutually orthogonal one-factorizations of the underlying graph. Let 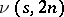 denote the maximum value of
denote the maximum value of 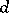 such that an
such that an 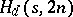 exists. Very little is known about upper bounds for
exists. Very little is known about upper bounds for 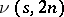 . It is easy to see that
. It is easy to see that 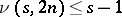 , and it has been conjectured that
, and it has been conjectured that 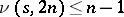 . See [a3], [a2] for results on
. See [a3], [a2] for results on 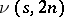 and existence results on
and existence results on 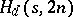 .
.
The survey article [a3] includes results and references on Howell designs.
References
| [a1] | B.A. Anderson, P.J. Schellenberg, D.R. Stinson, "The existence of Howell designs of even side" J. Combin. Th. A , 36 (1984) pp. 23–55 |
| [a2] | J.H. Dinitz, "Howell designs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 381–385 |
| [a3] | J.H. Dinitz, D.R. Stinson, "Room squares and related designs" J.H. Dinitz (ed.) D.R. Stinson (ed.) , Contemporary Design Theory: A Collection of Surveys , Wiley (1992) pp. 137–204 |
| [a4] | E.R. Lamken, S.A. Vanstone, "The existence of skew Howell designs of side 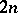 and order and order 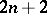 " J. Combin. Th. A , 54 (1990) pp. 20–40 " J. Combin. Th. A , 54 (1990) pp. 20–40 |
| [a5] | D.R. Stinson, "The existence of Howell designs of odd side" J. Combin. Th. A , 32 (1982) pp. 53–65 |
Howell design. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Howell_design&oldid=37181
 0
0 2
2 1
1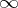 0
0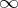 3
3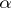 2
2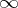 1
1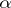 3
3