Value-distribution theory
2020 Mathematics Subject Classification: Primary: 30D35 [MSN][ZBL]
Nevanlinna theory
The theory of the distribution of values of meromorphic functions developed in the 1920's by R. Nevanlinna (see [1]). The basic problem is the study of the set 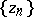 of points in a domain
of points in a domain 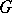 at which a function
at which a function 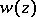 takes a prescribed value
takes a prescribed value  (so-called
(so-called  -points), where
-points), where 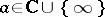 .
.
Basic concepts.
The fundamental aspects of Nevanlinna theory can be illustrated by taking the case where 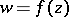 is a transcendental meromorphic function on the open complex plane
is a transcendental meromorphic function on the open complex plane  . Let
. Let 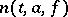 denote the number of
denote the number of  -points of
-points of 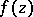 (counted with multiplicities) lying in the disc
(counted with multiplicities) lying in the disc 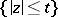 . Further, for any
. Further, for any 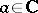 , define
, define
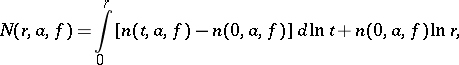 |
 |
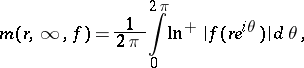 |
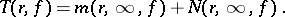 |
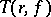 is called the Nevanlinna characteristic (or characteristic function) of
is called the Nevanlinna characteristic (or characteristic function) of 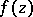 . The function
. The function 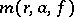 describes the average rate of convergence of
describes the average rate of convergence of 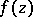 to
to  as
as 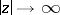 , and the function
, and the function 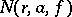 describes the average density of the distribution of the
describes the average density of the distribution of the  -points of
-points of 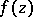 . The following theorem yields a geometric interpretation of the Nevanlinna characteristic
. The following theorem yields a geometric interpretation of the Nevanlinna characteristic 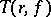 . Let
. Let 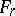 denote the part of the Riemann surface of
denote the part of the Riemann surface of 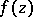 corresponding to the disc
corresponding to the disc 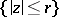 , and let
, and let  be the spherical area of the surface
be the spherical area of the surface 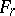 . Then
. Then
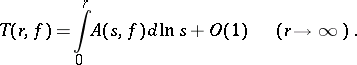 |
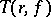 can be used to determine the order of growth
can be used to determine the order of growth 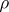 of
of  and its lower order of growth
and its lower order of growth 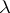 :
:
 |
Nevanlinna's first main theorem. As 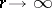 ,
,
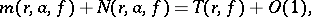 |
that is, up to a term that is bounded as  , the left-hand side takes the constant value
, the left-hand side takes the constant value  (whatever the value of
(whatever the value of  ). In this sense, all values
). In this sense, all values 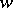 of the meromorphic function
of the meromorphic function 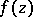 are equivalent. Of special interest is the behaviour of the function
are equivalent. Of special interest is the behaviour of the function 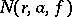 as
as 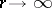 . In value-distribution theory, use is made of the following quantitative measures of growth of the functions
. In value-distribution theory, use is made of the following quantitative measures of growth of the functions  and
and 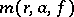 relative to the growth of the characteristic
relative to the growth of the characteristic 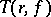 :
:
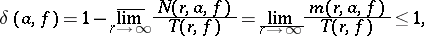 |
 |
The quantity 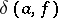 is called the Nevanlinna defect of
is called the Nevanlinna defect of 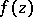 at
at  and
and 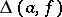 is called the Valiron defect of
is called the Valiron defect of 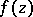 at
at  . Let
. Let
 |
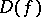 is called the set of deficient values (cf. Defective value) of
is called the set of deficient values (cf. Defective value) of 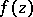 in the sense of Nevanlinna, and
in the sense of Nevanlinna, and 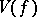 is called the set of deficient values of
is called the set of deficient values of  in the sense of Valiron. Nevanlinna's theorem on the magnitudes of the defects and on the set of deficient values of
in the sense of Valiron. Nevanlinna's theorem on the magnitudes of the defects and on the set of deficient values of 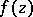 is as follows. For an arbitrary meromorphic function
is as follows. For an arbitrary meromorphic function 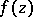 : a) the set
: a) the set 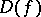 is at most countable; and b) the defects of
is at most countable; and b) the defects of  satisfy the relation
satisfy the relation
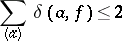 | (1) |
(the defect relation). The constant 2 figuring in (1) is the Euler characteristic of the extended complex plane 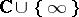 , which is covered by the Riemann surface of
, which is covered by the Riemann surface of 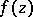 .
.
The structure of the set 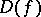 .
.
Nevanlinna's assertion that the set 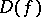 is at most countable cannot be strengthened. In fact, given any finite or countable set of points
is at most countable cannot be strengthened. In fact, given any finite or countable set of points 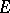 in the extended complex plane and any value of
in the extended complex plane and any value of 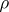 ,
, 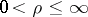 , there is a meromorphic function
, there is a meromorphic function  of order
of order  for which
for which 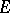 coincides with
coincides with 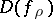 . For meromorphic functions whose lower order is zero,
. For meromorphic functions whose lower order is zero, 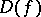 can contain at most one point. Thus, the question on the structure of
can contain at most one point. Thus, the question on the structure of 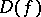 is completely solved.
is completely solved.
Moreover, it can be shown that for any 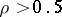 there is an entire function
there is an entire function 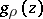 of order
of order 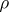 for which the set
for which the set 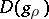 is countable. Entire functions of lower order
is countable. Entire functions of lower order 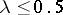 cannot have finite deficient values.
cannot have finite deficient values.
The structure of the set 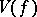 .
.
study of the set 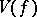 of Valiron deficient values is as yet (1992) incomplete. G. Valiron showed that there is an entire function
of Valiron deficient values is as yet (1992) incomplete. G. Valiron showed that there is an entire function 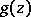 of order one for which the set
of order one for which the set 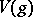 has the cardinality of the continuum. On the other hand, it can be shown that, for an arbitrary meromorphic function
has the cardinality of the continuum. On the other hand, it can be shown that, for an arbitrary meromorphic function 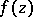 , the set
, the set  always has zero logarithmic capacity.
always has zero logarithmic capacity.
For every set 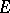 of class
of class 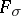 of zero logarithmic capacity there is an entire function
of zero logarithmic capacity there is an entire function 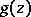 of infinite order for which
of infinite order for which 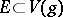 .
.
Properties of defects of meromorphic functions of finite lower order.
For meromorphic functions of infinite lower order, the defects do not, in general, satisfy any relations other than the defect relation (1). However, if one restricts to meromorphic functions of finite lower order, then the picture changes considerably. In fact, if 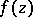 has finite lower order
has finite lower order 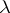 , then for any
, then for any 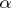 ,
, 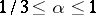 ,
,
 | (2) |
where the constant 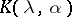 depends only on
depends only on 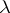 and
and 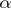 . On the other hand, there are meromorphic functions of finite lower order such that the series on the left-hand side of (2) diverges when
. On the other hand, there are meromorphic functions of finite lower order such that the series on the left-hand side of (2) diverges when 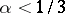 . For a meromorphic function
. For a meromorphic function 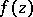 of lower order
of lower order 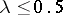 , the existence of a deficient value
, the existence of a deficient value  such that
such that 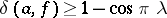 influences its asymptotic properties: such a function cannot have other deficient values.
influences its asymptotic properties: such a function cannot have other deficient values.
The inverse problem of value-distribution theory.
In a somewhat simplified form it is possible to formulate the inverse problem of value-distribution theory in any class 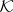 of meromorphic functions in the following way. Every point of a certain sequence
of meromorphic functions in the following way. Every point of a certain sequence 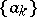 in the extended complex plane is assigned a number
in the extended complex plane is assigned a number 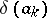 ,
, 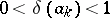 , in such a way that
, in such a way that  . It is required to find a meromorphic function
. It is required to find a meromorphic function 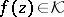 such that
such that 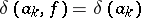 ,
, 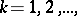 and
and 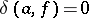 for each
for each 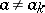 ,
, 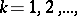 or to prove that
or to prove that 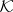 contains no such function. The inverse problem has been completely solved in the affirmative in the class of entire functions of infinite lower order and in the class of meromorphic functions of infinite lower order. In the solution of the inverse problem in the class of meromorphic functions of finite lower order there arise specific difficulties, due to the fact that in this case the defects satisfy further relations (like (2)) in addition to (1).
contains no such function. The inverse problem has been completely solved in the affirmative in the class of entire functions of infinite lower order and in the class of meromorphic functions of infinite lower order. In the solution of the inverse problem in the class of meromorphic functions of finite lower order there arise specific difficulties, due to the fact that in this case the defects satisfy further relations (like (2)) in addition to (1).
The growth of meromorphic functions.
Given a meromorphic function 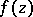 , let
, let
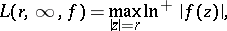 |
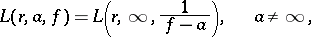 |
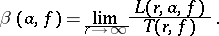 |
 is called the deviation of
is called the deviation of  from
from  , and the set
, and the set  is called the set of positive deviations of
is called the set of positive deviations of 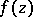 ;
; 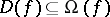 . It is known that if
. It is known that if  is an entire function of finite order
is an entire function of finite order 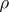 , then
, then
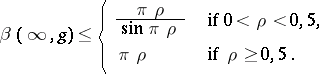 |
Thus, there is the following result: If a meromorphic function 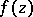 has finite lower order
has finite lower order  , then a)
, then a)  is at most countable; b) for each
is at most countable; b) for each  ,
,
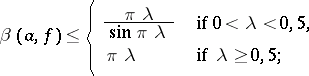 |
c) for any 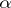 ,
, 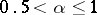 ,
,
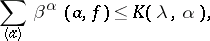 |
where the constant  depends only on
depends only on 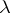 and
and  ; and d)
; and d) 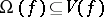 .
.
Moreover, there exist meromorphic functions of infinite lower order for which the set 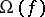 has the cardinality of the continuum. For any meromorphic function
has the cardinality of the continuum. For any meromorphic function 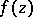 , the set
, the set 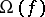 (like
(like 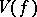 ) has zero logarithmic capacity. The following theorem characterizes the differences between
) has zero logarithmic capacity. The following theorem characterizes the differences between 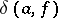 and
and 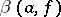 : For any
: For any 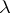 ,
, 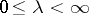 , there is a meromorphic function
, there is a meromorphic function 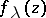 of lower order
of lower order 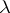 such that for some
such that for some  ,
,
 |
Exceptional values of meromorphic functions in the sense of Picard and Borel.
 is called an exceptional value of a meromorphic function
is called an exceptional value of a meromorphic function 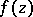 in the sense of Picard if the number of
in the sense of Picard if the number of  -points of
-points of  in
in  is finite. The value
is finite. The value  is called an exceptional value of
is called an exceptional value of 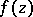 in the sense of Borel if
in the sense of Borel if 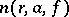 increases more slowly (in a certain sense) than
increases more slowly (in a certain sense) than 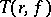 as
as 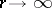 . A non-constant meromorphic function cannot have more than two Borel (and hence Picard) exceptional values.
. A non-constant meromorphic function cannot have more than two Borel (and hence Picard) exceptional values.
The value-distribution theory of holomorphic mappings of complex manifolds is being successfully developed as a higher-dimensional analogue of Nevanlinna theory (see [6], [7]), as is the value-distribution theory of minimal surfaces (see [9], [10]).
The distribution of values of functions meromorphic in a disc.
The value-distribution theory of meromorphic functions in the open complex plane has been described above; this is the parabolic case. A theory of growth and value distribution can also be set up in the hyperbolic case, that is, when 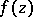 is a function meromorphic in the unit disc
is a function meromorphic in the unit disc  (see [1], [8]). In this case, the functions
(see [1], [8]). In this case, the functions 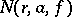 ,
, 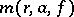 ,
,  , and
, and  are defined for
are defined for 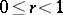 , just as in the parabolic case. The Nevanlinna and Valiron defects of
, just as in the parabolic case. The Nevanlinna and Valiron defects of  at a point
at a point  are thus defined as follows:
are thus defined as follows:
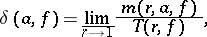 |
 |
The quantity
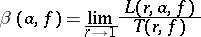 |
is called the deviation of 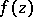 with respect to
with respect to  .
.
Let 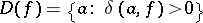 ,
, 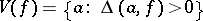 and
and 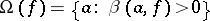 .
.
The main properties of  ,
, 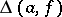 and
and 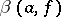 and of the structure of the sets
and of the structure of the sets 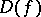 ,
, 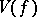 and
and 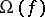 in the parabolic case carry over to the hyperbolic case, but only for those functions for which
in the parabolic case carry over to the hyperbolic case, but only for those functions for which 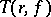 increases rapidly (in a certain sense) as
increases rapidly (in a certain sense) as  .
.
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | W.K. Hayman, "Meromorphic functions" , Clarendon Press (1964) |
| [3] | N.U. Arakelyan, "Entire functions of infinite order with an infinite set of deficient values" Soviet Math. Dokl. , 7 : 5 (1966) pp. 1303–1306 Dokl. Akad. Nauk SSSR , 170 : 5 (1966) pp. 999–1002 |
| [4] | A.A. Gol'dberg, I.V. Ostrovskii, "Value distribution of meromorphic functions" , Moscow (1970) (In Russian) |
| [5a] | V.I. Petrenko, "The study of the structure of the set of positive deviations of meromorphic functions" Math. USSR Izv. , 3 : 6 (1969) pp. 1251–1270 Izv. Akad. Nauk SSSR, Ser. Mat. , 33 : 6 (1969) pp. 1330–1348 |
| [5b] | V.I. Petrenko, "A study of the structure of the set of positive deviations of meromorphic functions" Math. USSR Izv. , 4 : 1 (1970) pp. 31–57 Izv. Akad. Nauk SSSR, Ser. Mat. , 34 : 1 (1970) pp. 31–56 |
| [6] | P. Griffiths, J. King, "Nevanlinna theory and holomorphic mappings between algebraic varieties" Acta Math. , 130 (1975) pp. 145–220 |
| [7] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [8] | V.P. Petrenko, "The growth of meromorphic functions" , Khar'kov (1978) (In Russian) |
| [9] | V.P. Petrenko, "On the growth and distribution of values of minimal surfaces" Dokl. Akad. Nauk SSSR , 255 : 1 (1981) pp. 40–42 (In Russian) |
| [10] | E.F. Beckenbach, G.A. Hutchison, "Meromorphic minimal surfaces" Pacific J. Math. , 28 : 1 (1969) pp. 17–47 |
Comments
The solution of the inverse problem of value-distribution theory (in a form sharper than that stated above) is due to D. Drasin [a1]; the inverse problem for entire functions had been solved previously by W.H.J. Fuchs and W.K. Hayman (cf. [2], Chapt. 4). To Drasin [a2] is also due the characterization of functions of finite lower order for which 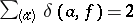 . That the sum in (2) is finite for
. That the sum in (2) is finite for 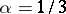 was proved by A. Weitsman [a3]; earlier, Hayman had shown that this was true for
was proved by A. Weitsman [a3]; earlier, Hayman had shown that this was true for 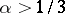 . On the other hand, there are meromorphic functions of finite order for which the sum in (2) diverges for every
. On the other hand, there are meromorphic functions of finite order for which the sum in (2) diverges for every 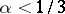 . For entire functions the situation is different. Recently, J.L. Lewis and J.-M. Wu have shown [a4] that there exists an
. For entire functions the situation is different. Recently, J.L. Lewis and J.-M. Wu have shown [a4] that there exists an 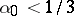 such that the sum in (2) converges for all
such that the sum in (2) converges for all 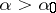 whenever
whenever 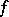 is an entire function of finite lower order. In fact, according to an old conjecture of N.U. Arakelyan, for such functions
is an entire function of finite lower order. In fact, according to an old conjecture of N.U. Arakelyan, for such functions 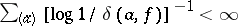 . This is perhaps the major open question concerning deficiencies.
. This is perhaps the major open question concerning deficiencies.
For a detailed discussion of value-distribution theory in several variables, see the articles in [a5] and [a7].
Around 1986 P. Vojta [a6] found a remarkable analogy between the main theorems in value-distribution theory and theorems from Diophantine approximations. Let 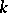 be an algebraic number field of degree
be an algebraic number field of degree  and
and 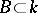 an infinite subset. Let
an infinite subset. Let 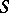 be a finite set of (suitably normalized) valuations on
be a finite set of (suitably normalized) valuations on  including the infinite ones. The guiding principle of the analogy is that the set of
including the infinite ones. The guiding principle of the analogy is that the set of  from Nevanlinna theory is replaced by
from Nevanlinna theory is replaced by 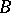 , the angles
, the angles 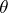 become elements of
become elements of 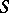 and
and 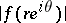 becomes
becomes 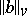 . See [a6] for a more complete dictionary. The analogue of
. See [a6] for a more complete dictionary. The analogue of 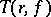 is
is  , the analogue of
, the analogue of 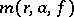 is
is 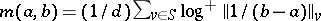 and
and  is translated into
is translated into 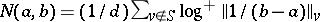 . The first main theorem then changes into
. The first main theorem then changes into 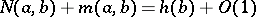 and this is a well-known property of heights in algebraic number theory. One can also introduce a defect,
and this is a well-known property of heights in algebraic number theory. One can also introduce a defect, 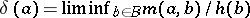 . The statement
. The statement 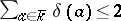 is precisely Roth's theorem on the approximation of algebraic numbers by elements from
is precisely Roth's theorem on the approximation of algebraic numbers by elements from 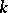 .
.
A similar translation of value distribution of meromorphic functions in several variables leads to a number of fascinating conjectures in the area of Diophantine approximations and Diophantine equations.
References
| [a1] | D. Drasin, "The inverse problem of Nevanlinna theory" Acta. Math. , 138 (1977) pp. 83–151 |
| [a2] | D. Drasin, "Proof of a conjecture of F. Nevanlinna concerning functions which have deficiency sum two" Acta Math. , 158 (1987) pp. 1–94 |
| [a3] | A. Weitsman, "A theorem on Nevanlinna deficiencies" Acta Math. , 125 (1972) pp. 41–52 |
| [a4] | J.L. Lewis, J.-M. Wu, "On conjectures of Arakelyan and Littlewood" J. d'Anal. Math. , 50 (1988) pp. 259–283 |
| [a5] | I. Laine (ed.) S. Rickman (ed.) , Value distribution theory , Lect. notes in math. , 981 , Springer (1983) |
| [a6] | P. Vojta, "Diophantine approximation and value distribution theory" , Lect. notes in math. , 1239 , Springer (1987) |
| [a7] | P.A. Griffiths, "Entire holomorphic mappings in one and several variables" , Annals Math. Studies , 85 , Princeton Univ. Press (1976) |
Value-distribution theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Value-distribution_theory&oldid=34917