Special functions

In the broad sense, a set of several classes of functions that arise in the solution of both theoretical and applied problems in various branches of mathematics.

In the narrow sense, special functions are the special functions of mathematical physics, which arise when solving partial differential equations by the method of separation of variables (cf. Separation of variables, method of).

Special functions can be defined by means of power series, generating functions, infinite products, repeated differentiation, integral representations, differential, difference, integral, and functional equations, trigonometric series, or other series in orthogonal functions.

The most important classes of special functions are the following: the gamma-function and the beta-function; hypergeometric functions and confluent hypergeometric functions (cf. Hypergeometric function; Confluent hypergeometric function); Bessel functions; Legendre functions; parabolic cylinder functions (cf. Parabolic cylinder function); integral sine and integral cosine functions; incomplete gamma- and beta-functions (cf. Incomplete gamma-function; Incomplete beta-function); probability integrals (cf. Probability integral); various classes of orthogonal polynomials in one or several variables; elliptic functions and integrals (cf. Elliptic function; Elliptic integral); Lamé functions (cf. Lamé function) and Mathieu functions; the Riemann zeta-function; automorphic functions (cf. Automorphic function); and some special functions of a discrete argument.

The theory of special functions is connected with the representation of groups (cf. Representation theory), with methods of integral representations based on the generalization of the Rodrigues formula for classical orthogonal polynomials, and with methods in probability theory.

There are tables of values of special functions and also tables of integrals and series.

References

[1]	A. Erdélyi et al. (ed.) , Higher transcendental functions , 1–3 , McGraw-Hill (1953–1955)
[2]	M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1970)
[3]	E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)
[4]	N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian)
[5]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6
[6]	A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960)
[7]	G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952)
[8]	E.W. Hobson, "The theory of spherical and ellipsoidal harmonics" , Cambridge Univ. Press (1931)
[9]	N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian)
[10]	A.F. Nikiforov, V.B. Ufarov, "Special functions of mathematical physics" , Birkhäuser (1988) (Translated from Russian)
[11]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)
[12]	W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1957–1971)
[13]	I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian)
[14]	A.P. Prudnikov, Yu.A. Brychkov, O.I. Marichev, "Integrals and series. Elementary functions" , Gordon & Breach (1986) (Translated from Russian)
[15]	A.P. Prudnikov, Yu.A. Brychkov, O.I. Marichev, "Integrals and series. Special functions" , Gordon & Breach (1986) (Translated from Russian)
[16]	A.P. Prudnikov, Yu.A. Brychkov, O.I. Marichev, "Integrals and series. Additional chapters" , Gordon & Breach (1987) (Translated from Russian)

Comments

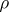Given a Lie group and a (matrix) representation of it, one can regard the matrix coefficients of 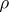as functions on 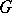. Many special functions can be seen as arising essentially in this way, and this point of view "explains" many of the special properties of special functions, e.g. various orthogonality relations. Cf. [9], [a1], [a4], and the encyclopaedic treatment [a2], vol. 1, for more details.

Many special functions have so-called -analogues, 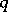-special functions. That means, roughly, that it is possible to insert a parameter 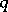to obtain a family of special functions in such a way that many of the characteristic properties of special functions are retained. These 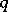-special functions correspond to quantum groups in the same way that special functions relate to Lie groups. Cf. the recent survey [a3], and [a2], vols. 2–3, for more details.

References

[a1]	W. Miller jr., "Lie theory and special functions" , Acad. Press (1968)
[a2]	N.Ya. Vilenkin, A.U. Klimyk, "Representations of Lie groups, special functions and integral transforms" , 1–3 , Kluwer (1991-) (Translated from Russian)
[a3]	T.H. Koornwinder, "Orthogonal polynomials in connection with quantum groups" P. Nevai (ed.) , Orthogonal polynomials: theory and practice , Kluwer (1990) pp. 257–292
[a4]	A. Wawrzyńczyk, "Group representations and special functions" , Reidel (1984)
[a5]	H.M. Srivastava, B.R.K. Kashyap, "Special functions in queuing theory" , Acad. Press (1982)