Iteration methods
for a matrix eigen value problem
Methods for finding the eigen values and eigen vectors (or a principal basis) of a matrix, omitting the preliminary calculation of characteristic polynomials. These methods are substantially different for problems of average size, in which the matrices may entirely be stored in a computer memory, and for problems of high order, in which the information is usually stored in compact form.
The first iteration method was proposed by C.G.J. Jacobi [1] for the computation of the eigen values and eigen vectors of real symmetric matrices (cf. Rotation method). This method can be generalized to complex Hermitian matrices, and also to the larger class of normal matrices.
There is a number of generalizations of Jacobi's method to matrices of arbitrary form. The typical algorithm of this class consists of a sequence of elementary steps, performed according to the scheme
$$ \widetilde{A} _ {k+1} = S _ {k} ^ {-1} A _ {k} S _ {k} , $$
$$ A _ {k+1} = T _ {k} ^ {*} \widetilde{A} {} _ {k+1} ^ {*} T _ {k} . $$
The role of the similarity transformation with (elementary) matrix $ S $ consists here in reducing the Euclidean norm of the current matrix $ A _ {k} $, i.e. $ A _ {k+1} $ is nearer to being normal than $ A _ {k} $. For $ T _ {k} $ one usually takes a rotation matrix or its unitary analogue. The aim of the similarity transformation with this matrix is, as in Jacobi's classical method, in annihilating off-diagonal entries in a Hermitian matrix related with $ A _ {k+1} $, e.g. in the matrix $ A _ {k+1} + \widetilde{A} {} _ {k+1} ^ {*} $. The matrices $ A _ {k} $ converge, as $ k $ increases, to a matrix of diagonal or quasi-diagonal form, and the accumulated products of $ S _ {k} $ and $ T _ {k} $ give a matrix in which the columns are the approximate eigen vectors, or are base vectors of invariant subspaces of these matrix (cf. [2], [3]).
Along with the methods described above, algorithms of another class, so called power methods, have been developed. The most effective method in this direction, and the one that is most often used for solving problems of average size, is the QR-algorithm (cf. [4], ). The iterations of the QR-algorithm are performed according to the following scheme:
$$ \tag{1 } A _ {k} = Q _ {k} R _ {k} ,\ \ A _ {k+1} = R _ {k} Q _ {k} . $$
In it, $ Q _ {k} $ is an orthogonal or unitary, and $ R _ {k} $ is a right-triangular matrix. In the transition from $ A _ {k} $ to $ A _ {k+1} $ one first finds the orthogonal-triangular decomposition of $ A _ {k} $, after which $ Q _ {k} $ and $ R _ {k} $ are multiplied in reverse order. If $ \widetilde{Q} _ {k} = Q _ {1} \dots Q _ {k} $ and $ \widetilde{R} _ {k} = R _ {k} \dots R _ {1} $, then (1) implies
$$ \tag{2 } A _ {k+1} = \widetilde{Q} {} _ {k} ^ {*} A _ {1} \widetilde{Q} _ {k} ,\ \ A _ {1} ^ {k} = \widetilde{Q} _ {k} \widetilde{R} _ {k} . $$
Thus, the QR-algorithm generates a sequence of matrices $ A _ {k} $ that are orthogonally similar to the initial matrix $ A _ {1} $; moreover, the transforming matrix $ \widetilde{Q} _ {k} $ is the orthogonal component in the decomposition (2) of $ A _ {1} ^ {k} $.
When iterating by the scheme (1), the matrices $ A _ {k} $ converge to a right-triangular or quasi-triangular matrix, and the rate of convergence to zero of the subdiagonal entries is determined by the quotients between the absolute values of various eigen values and is, generally speaking, quite slow. To improve the convergence of the QR-algorithm one uses so-called shifts, which leads to the following variant of (1):
$$ \tag{3 } A _ {k} - \kappa _ {k} I = Q _ {r} R _ {k} ,\ \ A _ {k+1} = R _ {k} Q _ {k} + \kappa _ {k} I . $$
Usually, by the application of shifts (e.g. $ \kappa _ {k} = a _ {nn} ^ {(} k) $) one obtains a faster convergence to zero of the off-diagonal entries of the last row (asymptotically quadratic in the general case and cubic for Hermitian matrices), with corresponding fast stabilization of the diagonal entry $ ( n , n ) $. After the value of this entry has been established, further iteration is performed with the principal submatrix of order $ n - 1 $, etc. The eigen vectors of the resulting triangular matrix give, after multiplication by the accumulated product of the orthogonal matrices $ Q _ {k} $, the eigen vectors of the initial matrix $ A _ {1} $.
Iteration by (1) or (3) is applied to matrices that have previously been reduced to the so-called Hessenberg form. One says that a matrix $ A $ is in right Hessenberg form if $ a _ {ij} = 0 $ for $ i > j + 1 $. The QR-algorithm preserves the Hessenberg form, which generally reduces the cost of each iteration. There are other important possibilities for reducing the amount of calculation, e.g., by implicit use of shifts, which allow one to find complex conjugate eigen values of real matrices without going into complex arithmetic.
In problems of high order (from hundreds to thousands), the matrices are usually sparse, i.e. have a relatively few number of non-zero entries. Moreover, it is usually required to compute not all but only a few eigen values and corresponding eigen vectors. In a typical case the eigen values required are the largest or the smallest in absolute value.
The methods described above, based on similarity transformations, destroy the sparseness of the matrix and are thus not recommended. Methods in which the elementary transformation is multiplication of a matrix by a vector are fundamental to methods of high order. In their further description it is supposed in what follows that the eigen values of the matrix $ A $ are enumerated in order of decreasing absolute value:
$$ | \lambda _ {1} | \geq \dots \geq | \lambda _ {n} | . $$
The power method for determining an eigen value $ \lambda _ {1} $ of maximal absolute value has widest domain of applicability. Starting from an initial approximation $ x _ {0} $ one constructs a sequence of normalized vectors
$$ \tag{4 } x _ {k+1} = \rho _ {k} A x _ {k} ,\ \ \rho _ {k} = \frac{1}{\| A x _ {k} \| } . $$
This sequence converges to an eigen vector corresponding to $ \lambda _ {1} $ if: 1) all elementary divisors of $ A $ related to $ \lambda _ {1} $ are linear; 2) there are no other eigen values of the same absolute value; and 3) in the decomposition of $ x _ {0} $ with respect to a principal basis of $ A $ the component in the eigen space corresponding to $ \lambda _ {1} $ is non-trivial. However, the convergence of a power method is, as a rule, slow, and is determined by $ | \lambda _ {1} | / | \lambda _ {2} | $.
If an approximation $ \widetilde \lambda _ {0} $ to the desired eigen value $ \lambda _ {0} $ is known, then one obtains a faster convergence by the method of inverse iteration. Instead of (4), one constructs a sequence determined by
$$ \tag{5 } ( A - \widetilde \lambda _ {0} I ) x _ {k+1} = \rho _ {k} x _ {k} ,\ \ \| x _ {k} \| = 1 ,\ \ \textrm{ for all } k . $$
The method of inverse iteration is, basically, a power method for $ ( A - \widetilde \lambda _ {0} I ) ^ {-1} $, which has the strongly-dominating eigen value $ 1 / ( \widetilde \lambda - \lambda _ {0} ) $. However, the realization of (5) requires the solution to a linear system with matrix $ A - \widetilde \lambda _ {0} I $, and even when using special methods for sparse system this increases the demands on the computer memory in comparison to the power method.
So-called methods of simultaneous iteration are used in order to calculate groups of eigen values. They are generalizations of the power method, and instead of iterating one vector, one actually constructs iterations under $ A $ of an entire subspace. Stewart's method is a typical representative of this group of methods [6]. Suppose that the eigen values of $ A $ satisfy
$$ | \lambda _ {1} | \geq \dots \geq \ | \lambda _ {r} | > \ | \lambda _ {r+1} | \geq \dots \geq \ | \lambda _ {n} | . $$
One chooses an initial $ ( n \times r ) $- matrix $ Q _ {0} $ with orthogonal columns. One then constructs a sequence of matrices $ Q _ {k} $, starting from $ Q _ {0} $, by
$$ \tag{6 } \widetilde{Q} _ {k+1} = A Q _ {k} ,\ \ \widetilde{Q} _ {k+1} = {\tilde{\tilde{Q}} } _ {k+1} R _ {k+1} , $$
$$ Q _ {k+1} = {\tilde{\tilde{Q}} } _ {k+1} W _ {k+1} . $$
In the second formula, $ R _ {k+1} $ is a right-triangular $ ( r \times r ) $- matrix, and $ {\tilde{\tilde{Q}} } _ {k+1} $ has orthonormal columns. The aim of this decomposition, which need not be computed at every iteration, is that the linear independence of the columns of $ Q _ {k} $, which may in a practical sense be destroyed by multiple iteration under $ A $, is preserved. The third formula in (6) plays an important role in accelerating the convergence of the method. The orthogonal $ ( r \times r ) $- matrix $ W _ {k+1} $ participating in this formula has the following meaning. If $ B _ {k+1} $ denotes the $ ( r \times r ) $- matrix $ Q _ {k} ^ {*} A Q _ {k} $, then $ W _ {k+1} $ reduces $ B _ {k+1} $ to Schur form, i.e. to a right-triangular matrix. The matrix $ W _ {k+1} $ can be constructed using the QR-algorithm, its columns form a Schur basis of $ B _ {k+1} $, characterized by the fact that for each $ k $, $ 1 \leq k \leq r $, the linear span of the first $ k $ vectors forms an invariant subspace of $ B _ {k+1} $. The matrices $ Q _ {k} $ of Stewart's method converge to a matrix $ Q $ whose columns form a Schur basis for the invariant subspace of $ A $ corresponding to $ \lambda _ {1} \dots \lambda _ {r} $. Here, the convergence of the $ i $- th column is determined by the quotient $ | \lambda _ {r+1} | / | \lambda _ {i} | $.
In the case of a real symmetric matrix, additional possibilities arise. They are related to the treatment of eigen values as stationary points of the Rayleigh functional
$$ \tag{7 } \phi ( A , x ) = \ \frac{( A x , x ) }{( x , x ) } ,\ \ x \neq 0 . $$
Methods for unconstrained optimization of (7) can be used to determine extreme points of the spectrum. The theory thus obtained parallels that of the iteration methods for solving positive-definite linear systems, and leads to the same algorithms: coordinate relaxation, sequential overrelaxation, steepest descent, and conjugate gradients (cf. [7]).
The methods listed find the eigen values "one-after-one" . Lanczos' method is used to determine simultaneously groups of eigen values for a symmetric matrix [8]; the method was proposed for the tri-diagonalization of a symmetric matrix of order $ n $. The following observations lie at the foundation of the method: If a sequence of vectors $ p _ {0} , A p _ {0} \dots A ^ {n-1} p _ {0} $ is linearly independent, then the matrix can be reduced to tri-diagonal form $ T _ {n} $ in the basis $ q _ {1} \dots q _ {n} $ obtained by orthonormalization of this sequence. The vectors $ q _ {k} $ are constructed by three-term recurrence formulas:
$$ \beta _ {k} q _ {k+1} = \ A q _ {k} - \beta _ {k-1} q _ {k-1} - \alpha _ {k} q _ {k} , $$
in which the coefficients $ \alpha _ {k} $, $ \beta _ {k} $, $ k = 1 \dots n $, determine $ T _ {n} $. After $ k $ steps in the orthogonalization process, the vectors $ q _ {1} \dots q _ {k} $ as well as the principal submatrix $ T _ {k} $ of $ T _ {n} $ are known. In many cases, already for $ k \ll n $ part of the eigen values of $ T _ {k} $ are sufficiently good approximations to some eigen values of $ T _ {n} $. The corresponding eigen vectors of $ T _ {k} $ can be used to construct approximate eigen vectors to $ A $. If the required accuracy has not yet been achieved, one may choose another initial approximation $ \widetilde{p} _ {0} $ in the linear span of $ q _ {1} \dots q _ {k} $ and repeat the process, making $ \widetilde{k} $ steps, etc. Lanczos' method in an iterative treatment consists of this (cf. [9]).
The search for interior points of the spectrum of a sparse matrix $ A $ of high order requires the ability to invert matrices of the form $ A - \tau I $ for a sequence $ \{ \tau _ {k} \} $, [10].
References
| [1] | C.G.J. Jacobi, "Ueber ein leichtes Verfahren, die in der Theorie der Säcularstörungen vorkommenden Gleichungen numerisch auflösen" J. Reine Angew. Math. , 30 (1846) pp. 51–94 |
| [2] | P.J. Eberlein, "A Jacobi-like method for the automatic computation of eigenvalues and eigenvectors of an arbitrary matrix" J. Soc. Industr. Appl. Math. , 101 : 1 (1962) pp. 74–88 |
| [3] | V.V. Voevodin, "The solution of the complete eigenvalue problem by a generalized rotation method" Zh. Vychish. Met. i Programmirov. , 3 (1965) pp. 89–105 (In Russian) |
| [4] | V.N. Kublanovskaya, "On some algorithms for the solution of the complete eigenvalue problem" USSR Comp. Math. Math. Phys. , 3 (1961) pp. 637–657 Zh. Vychisl. Mat. i Mat. Fiz. , 1 : 4 (1961) pp. 555–570 |
| [5a] | J.G.F. Francis, "The QR transformation: A unitary analogue to the LR transformation I" Comput. J. , 4 : 3 (1961) pp. 265–271 |
| [5b] | J.G.F. Francis, "The QR transformation: A unitary analogue to the LR transformation II" Comput. J. , 4 : 4 (1962) pp. 332–345 |
| [6] | G.W. Stewart, "Simultaneous iteration for computing invariant subspaces of non-Hermitian matrices" Numer. Math. , 25 : 2 (1976) pp. 123–136 |
| [7] | A. Ruhe, "Computation of eigenvalues and eigenvectors" , Springer (1977) |
| [8] | C. Lanczos, "An iteration method for the solution of the eigenvalue problem of linear differential and integral operators" J. Res. Nat. Bur. Standards , 45 : 4 (1950) pp. 255–282 |
| [9] | C.C. Paige, "Computational variants of the Lanczos method for the eigenproblem" J. Inst. Math. Appl. , 10 (1972) pp. 373–381 |
| [10] | T. Ericsson, A. Ruhe, "The spectral transformation Lánczos method for the numerical solution of large sparse generalized symmetric eigenvalue problems" Math. Comp. , 35 (1980) pp. 1251–1268 |
Comments
The Hessenberg form is not only preferable for its sparse structure, but also to guarantee convergence of the QR-algorithm. Moreover, by judicious choice of the shifts the convergence of the diagonal entries to the eigen values starts in principle at the last position, thus making it possible to proceed on a deflated matrix.
The Lanczos algorithm nowadays is one of the most powerful processes to compute eigen values of a large sparse matrix (not only "the interior points" ). The interesting aspect is that the computed vectors by no means form an orthogonal basis, rather they are steps in an (infinite) iteration process. Sometimes convergence to an eigen value temporarily halts; later on it is resumed. This is due to a (numerically) multiple eigen value. For more information see [a1].
The standard reference to numerical linear algebra is the text book [a7], which provides an excellent introduction to the methods surveyed in the article above. A more detailed treatment of the matrix eigen problem is given in [a8], [a2] and [a3]. Application of the various variants of Jacobi's method may be found in [a4] and [a5], and aspects of the QR-algorithm are discussed in
and [a10]. Additional references on the Lanczos method are [a9], [a11]. Finally, matrix eigen system Fortran routines are collected in [a6].
See also Complete problem of eigen values; Partial problem of eigen values
References
| [a1] | J.K. Cullum, R.A. Willoughby, "Lanczos algorithms for large symmetric eigenvalue computations" , Birkhäuser (1985) |
| [a2] | B.N. Parlett, "The symmetric eigenvalue problem" , Prentice-Hall (1980) |
| [a3] | J.H. Wilkinson, "The algebraic eigenvalue problem" , Clarendon Press (1965) |
| [a4] | P.J. Eberlein, "Solution of the complex eigenproblem by a norm-reducing Jacobi-type method" Numer. Math. , 14 (1970) pp. 232–245 |
| [a5] | G.E. Forsythe, P. Henrici, "The cyclic Jacobi method for computing the principal values of a complex matrix" Trans. Amer. Math. Soc. , 94 (1960) pp. 1–23 |
| [a6] | B.S. Garbow, J.M. Doyle, J.J. Dongara, C.B. Moler, "Matrix eigensystem routines: EISPACK guide extensions" , Springer (1972) |
| [a7] | G.H. Golub, C.F. van Loan, "An analysis of the total least squares problem" SIAM J. Numer. Math. , 17 (1980) pp. 883–893 |
| [a8] | A.R. Gourlay, G.A. Watson, "Computational methods for matrix eigenproblems" , Wiley (1977) |
| [a9] | C.C. Paige, "Computational invariants of the Lanczos method for the eigenproblem" J. Inst. Math. Appl. , 10 (1972) pp. 373–381 |
| [a10] | B.N. Parlett, "Convergence of the QR algorithm" Numer. Math. , 7 (1965) pp. 187–193 (Correction in  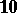 (1967), 163–164) (1967), 163–164) |
| [a11] | B.N. Parlett, D.S. Scott, "The Lanczos algorithm with selective orthogonalization" Math. Comp. , 33 (1979) pp. 217–238 |
Iteration methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Iteration_methods&oldid=51657