Kolmogorov inequality

Kolmogorov's inequality in approximation theory is a multiplicative inequality between the norms in the spaces $ L _ {s} ( J) $ of functions and their derivatives on the real axis (or half-line):

$$ \| x ^ {(} k) \| _ {L _ {q} } \leq \ C \| x \| _ {L _ {r} } ^ \nu \cdot \| x ^ {(} n) \| _ {L _ {p} } ^ {1 - \nu } , $$

where

$$ 0 \leq k < n,\ \ \nu = \ \frac{n - k - p ^ {-} 1 + q ^ {-} 1 }{n - p ^ {-} 1 + r ^ {-} 1 } , $$

and $ C $ does not depend on $ x $. Such inequalities were first studied by G.H. Hardy (1912), J.E. Littlewood (1912), E. Landau (1913), and J. Hadamard (1914). A.N. Kolmogorov [1] obtained the best possible constant $ C $ for the most important case $ J = ( - \infty , + \infty ) $, $ p = q = r = \infty $ and arbitrary $ k $, $ n $.

Kolmogorov's inequality is connected with problems of best numerical differentiation and the stable calculation of the (unbounded) operator $ D ^ {k} $ of $ k $- fold differentiation. In fact, the modulus of continuity

$$ \omega ( \delta ) = \ \sup \ \{ {\| x ^ {(} k) \| _ {L _ {q} } } : { \| x \| _ {L _ {r} } \leq \delta ,\ \| x ^ {(} n) \| _ {L _ {p} } \leq 1 } \} $$

of the operator $ D ^ {k} $ on the class $ \{ {x \in L _ {r} } : {\| x ^ {(} n) \| _ {L _ {p} } \leq 1 } \} $ is expressed by the formula $ \omega ( \delta ) = \omega ( 1) \delta $, that is, Kolmogorov's inequality holds with constant $ C = \omega ( 1) $.

Kolmogorov's inequality is a special case of inequalities relating to the imbedding of classes of differentiable functions (see Imbedding theorems).

References

[1]	A.N. Kolmogorov, "On inequalities between the upper bounds of the successive derivatives of an arbitrary function on an infinite interval" Transl. Amer. Math. Soc. (1) , 2 (1962) pp. 233–243 Uchen. Zap. Moskov. Univ. Mat. , 3 : 30 (1939) pp. 3–16
[2]	S.B. Stechkin, "Best approximation of linear operators" Math. Notes , 1 (1967) pp. 91–99 Mat. Zametki , 1 : 2 (1967) pp. 137–148
[3]	L.V. Taikov, "Kolmogorov-type inequalities and the best formulas for numerical differentiation" Math. Notes , 4 (1968) pp. 631–634 Mat. Zametki , 4 : 2 (1968) pp. 233–238
[4]	V.V. Arestov, "Precise inequalities between norms of functions and their derivatives" Acta Sci. Math. , 33 (1972) pp. 243–267 (In Russian)

Comments

Landau's work [a1] should be mentioned in particular: he initiated in 1913 a new kind of extremum problem, i.e. obtaining sharp inequalities between the supremum norms of derivatives. The analogue of Kolmogorov's theorem for the half-line $ \mathbf R _ {+} $ has been established by I.J. Schoenberg and A. Cavaretta [a3]; cf. also [a2]. For a beautiful survey concerning these problems see [a4]. Norm inequalities for the difference operator have been studied rather recently; see e.g. [a5].

References

[a1]	E. Landau, "Einige Ungleichungen für zweimal differentierbare Funktionen" Proc. London Math. Soc. , 13 (1913) pp. 43–49
[a2]	H.G. ter Morsche, "Interpolation and extremal properties of 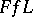-spline functions" , Univ. Eindhoven (1982) (Thesis)
[a3]	I.J. Schoenberg, A. Cavaretta, "Solution of Landau's problem concerning higher derivatives on the halfline" , Proc. Internat. Conf. Constructive Function Theory , Bulgarian Acad. Sci. (1972) pp. 297–308
[a4]	I.J. Schoenberg, "The elementary cases of Landau's problem of inequalities between derivatives" Amer. Math. Monthly , 80 (1973) pp. 121–158
[a5]	H.G. Kaper, B.E. Spellman, "Best constants in norm inequalities for the difference operator" Trans. Amer. Math. Soc. , 299 (1987) pp. 351–372

Kolmogorov's inequality in probability theory is an inequality for the maximum of sums of independent random variables. It is a generalization of the classical Chebyshev inequality in probability theory. Let $ X _ {1} \dots X _ {n} $ be independent random variables with finite mathematical expectations $ a _ {n} = {\mathsf E} X _ {n} $ and variances $ \sigma _ {n} ^ {2} = {\mathsf D} X _ {n} $. Then, for any $ \epsilon > 0 $,

$$ {\mathsf P} \left \{ \max _ {1 \leq m \leq n } \ \left | \sum _ { k= } 1 ^ { m } ( X _ {k} - a _ {k} ) \ \right | \geq \epsilon \right \} \leq \frac{1}{\epsilon ^ {2} } \sum _ { k= } 1 ^ { n } \sigma _ {k} ^ {2} , $$

and if the variables are bounded ( $ | X _ {i} | \leq c $ with probability $ 1 $), then

$$ 1 - \frac{( \epsilon + 2 c ) ^ {2} }{\sum _ { k= } 1 ^ { n } \sigma _ {k} ^ {2} } \leq {\mathsf P} \left \{ \max _ {1 \leq m \leq n } \ \left | \sum _ { k= } 1 ^ { m } ( X _ {k} - \sigma _ {k} ) \ \right | \geq \epsilon \right \} . $$

These inequalities were established by A.N. Kolmogorov . Kolmogorov's inequality is remarkable both as to its proof (the method of argument in probability theory is new) and in the result itself (the estimate for the maximum of the sums is the same as that for the last sum in the Chebyshev inequality).

In the proof of the Kolmogorov inequality essential use is made of the properties of conditional mathematical expectations of functions and sums $ S _ {k+} p $ under the condition that $ X _ {1} \dots X _ {k} $ are fixed. These properties arise from the independence of the $ X _ {k} $.

The Kolmogorov inequality admits numerous generalizations, of which one can mention the following.

1) The Kolmogorov inequality remains true if the condition of independence of the variables $ X _ {n} $ is replaced by the condition that $ \{ X _ {n} \} $ is an absolutely-unbiased sequence, that is, if the sequence of sums $ S _ {n} = \sum _ {k=} 1 ^ {n} X _ {k} $ forms a martingale.

2) If $ g ( t) \geq 0 $ is a convex monotone function and $ {\mathsf E} g ( | S _ {n} | ) < \infty $, then

$$ {\mathsf P} \left \{ \max _ {1 \leq m \leq n } \ | S _ {m} | \geq \epsilon \right \} \leq {\mathsf E} g ( | S _ {n} | ) \frac{1}{g ( \epsilon ) } . $$

3) If the $ X _ {k} $, $ k = 1 \dots n $, are symmetric about the origin, then

$$ {\mathsf P} \left \{ \max _ {1 \leq m \leq n } \ | S _ {m} | \geq \epsilon \right \} \leq 2 {\mathsf P} \{ | S _ {n} | \geq \epsilon \} ; $$

see Lévy inequality.

4) For arbitrary independent random variables $ X _ {1} , X _ {2} \dots $

$$ {\mathsf P} \left \{ \max _ {1 \leq m \leq n } \ | S _ {m} | > \delta + \epsilon \right \} \leq \frac{1}{1 - p } {\mathsf P} \{ | S _ {n} | > \epsilon \} , $$

provided that $ \delta > 0 $ and $ 0 < p < 1 $ are chosen so that $ {\mathsf P} \{ | S _ {m} | > \delta \} \leq p $ for all $ m $, $ 1 \leq m \leq n $.

The following property of sums of independent variables can be seen in all versions of Kolmogorov's inequality: The "spread" of the maximum sum has the same order of magnitude as the "spread" of the final sum.

Just as the Chebyshev inequality is applied in the derivation of the law of large numbers, so the Kolmogorov inequality is applied in the proof of the strong law of large numbers (the Kolmogorov criterion for convergence of $ S _ {n} / n \rightarrow 0 $ almost-everywhere). The proof of convergence theorems for series of random variables is based on the use of the Kolmogorov inequality.

References

[1a]	A.N. Kolmogorov, "Ueber die Summen durch den Zufall bestimmter unabhängiger Grössen" Math. Ann. , 99 (1928) pp. 309–319
[1b]	A.N. Kolmogorov, "Bemerkungen zur meiner Arbeit "Ueber die Summen durch den Zufall bestimmter unabhängiger Grössen" " Math. Ann. , 102 (1929) pp. 484–488
[2]	A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from German)
[3]	M. Loève, "Probability theory" , Princeton Univ. Press (1963)

A.V. Prokhorov

References

[a1]	W. Feller, "An introduction to probability theory and its applications", 2 , Wiley (1966) pp. Sect. VII.8