Zak transform

Gel'fand mapping, - representation, Weil–Brezin mapping

The Zak transform was discovered by several people in different fields and was called by different names, depending on the field in which it was discovered. It was called the "Gel'fand mapping" in the Russian literature because I.M. Gel'fand [a3] introduced it in his work on eigenfunction expansions associated with Schrödinger operators with periodic potentials. In 1967, almost 17 years after the publication of Gel'fand's work, the transform was rediscovered independently by a solid-state physicist, J. Zak, who called it the "k-q representation" . Zak introduced this representation to construct a quantum-mechanical representation for the motion of a Bloch electron in the presence of a magnetic or electric field [a8], [a9]. It has also been said [a7] that some properties of another version of the Zak transform, called the "Weil–Brezin mapping" in [a1], [a7], were even known to the mathematician C.F. Gauss. Nevertheless, there seems to be a general consent among experts in the field to call it the Zak transform, since Zak was indeed the first to systematically study that transform in a more general setting and recognize its usefulness.

The Zak transform of a function is defined by

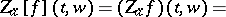(a1)

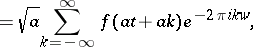where and and 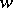are real. When 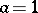, one denotes by .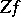

If 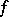represents a signal, then its Zak transform can be considered as a mixed time-frequency representation of 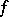, and it can also be considered as a generalization of the discrete Fourier transform of 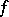in which an infinite sequence of samples in the form , , 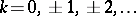is used (cf. also Fourier transform).

Examples.

If and 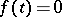outside 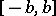, , 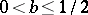then , .

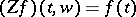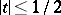The Zak transform of the Gaussian function

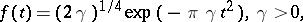is easily shown to be

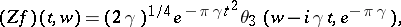where 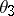is the third theta-function, defined by

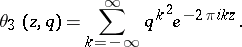Existence.

If is integrable or square integrable (cf. Integrable function), its Zak transform exists almost everywhere. In particular, if is a continuous function such that 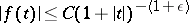, for some , for all , then its Zak transform exists and defines a continuous function.

Elementary properties.

1) (linearity): for any complex numbers and ,

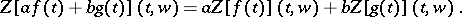2) (translation): for any integer ,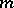

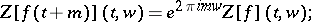in particular,

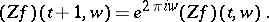3) (modulation):

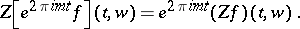4) (periodicity): The Zak transform is periodic in with period one, that is,

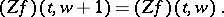5) (translation and modulation): By combining 2) and 3) one obtains

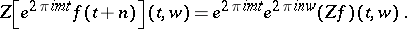6) (conjugation):

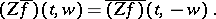7) (symmetry): If 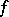is even (cf. also Even function), then

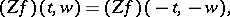and if is odd, then

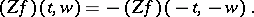From 6) and 7) it follows that if is real-valued and even, then

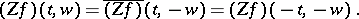Because of 2) and 4), the Zak transform is completely determined by its values on the unit square .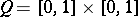

8) (convolution): Let

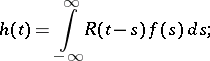then

Analytic properties.

If 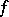is a continuous function such that 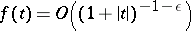as 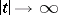for some , then 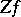is continuous on 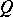. A rather peculiar property of the Zak transform is that if is continuous, it must have a zero in 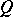. The Zak transform is a unitary transformation from onto ; see [a10], p. 481.

Inversion formulas.

The following inversion formulas for the Zak transform follow easily from the definition, provided that the series defining the Zak transform converges uniformly (cf. also Uniform convergence):

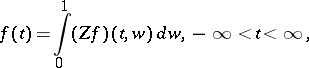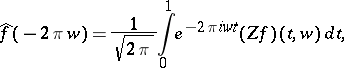and

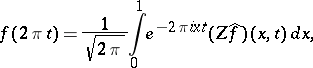where 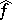is the Fourier transform of , given by

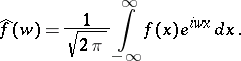Applications.

The Zak transform has been used successfully in various applications in physics, such as in the study of the coherent states representation in quantum field theory [a6], and in electrical engineering, such as in time-frequency representation of signals and in digital data transmission; see [a4], [a5].

The applications of the Zak transform are not limited to only physics and engineering. More recent applications of it in mathematics have proved to be very useful; in particular, to simplify proofs of some important results. A case in point is the Gabor representation problem. The Gabor representation problem can be stated as follows: Given 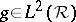and two real numbers, , 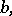different from zero, is it possible to represent any function 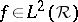by a series of the form

where 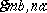are the Gabor functions, defined by

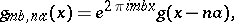and are constants? And under what conditions is the representation unique?

The Zak transform has been used successfully to study the orthogonality and the completeness of Gabor frames in the crucial case where 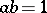; see [a2], [a10].

References

[a1]	L. Auslander, R. Tolimieri, "Radar ambiguity functions and group theory" SIAM J. Math. Anal. , 16 (1985) pp. 577–601
[a2]	I. Daubechies, "Ten lectures on wavelets" , SIAM (1992)
[a3]	I. Gel'fand, "Eigenfunction expansions for an equation with periodic coefficients" Dokl. Akad. Nauk. SSR , 76 (1950) pp. 1117–1120 (In Russian)
[a4]	A.J. Janssen, "The Zak transform: A signal transform for sampled time-continuous signals" Philips J. Research , 43 (1988) pp. 23–69
[a5]	A.J. Janssen, "Bargmann transform, Zak transform, and coherent states" J. Math. Phys. , 23 (1982) pp. 720–731
[a6]	J. Klauder, B.S. Skagerstam, "Coherent states" , World Sci. (1985)
[a7]	W. Schempp, "Radar ambiguity functions, the Heisenberg group and holomorphic theta series" Proc. Amer. Math. Soc. , 92 (1984) pp. 103–110
[a8]	J. Zak, "Finite translation in solid state physics" Phys. Rev. Lett. , 19 (1967) pp. 1385–1397
[a9]	J. Zak, "Dynamics of electrons in solids in external fields" Phys. Rev. , 168 (1968) pp. 686–695
[a10]	A.I. Zayed, "Function and generalized function transformations" , CRC (1996)