Alternating knots and links

Knots and links with an alternating diagram (cf. Knot and link diagrams), i.e. a projection in general position onto a plane such that, when successively traversing all components, the overpasses and underpasses succeed each other in alternation. Any diagram can be converted to an alternating diagram by changing the upper and lower branches through its double points.

Let 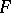be a Seifert surface. As distinct from the ordinary case, the inequality 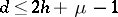, where 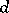is the degree of the Alexander polynomial (cf. Alexander invariants), 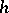is the genus of the Seifert surface and 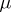is the number of components of the link 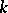, becomes an equality in the case of alternating knots and links. Accordingly, the genus of an alternating link can be computed from any one of its alternating diagrams, the Seifert surface being the surface of smallest genus. This also shows that if the diagram is normalized, i.e. if the projection plane does not contain a simple closed contour that intersects the diagram at one double point, the link is trivial (cf. Knot theory) if and only if the diagram contains no double points. If such a contour exists, it is possible, by rotating an internal part of the diagram through 180 degrees, to reduce the number of double points while preserving the alternating nature of the diagram. This yields an algorithm for solving the problem of triviality of alternating knots and links. Moreover, if the diagram is connected, the links do not become separated, since 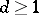, and the reduced Alexander polynomial of seperated links is zero. The Alexander matrix is computed as the incidence matrix of some graph, which implies [1], [2] that 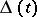is an alternating polynomial, i.e. its coefficients are non-zero and their signs alternate. If 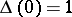, alternating knots and links are known as Neuwirth knots and links (cf. Neuwirth knot). The number of double points of a normalized diagram of an alternating knot or link is not larger than its determinant. The groups of alternating knots and links (cf. Knot and link groups) are represented as free products with amalgamation of two free groups of rank 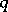by subgroups of rank 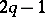. This representation is obtained with the aid of the van Kampen theorem, if the space of the link 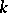is subdivided by the boundaries of regular neighbourhoods of the Seifert surface with respect to 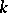, constructed over the alternating diagram. All knots of the standard table (cf. Knot table) with non-alternating diagrams are non-alternating knots. Most parallel knots, windings, etc., do not alternate.

References

[1]	K. Murasugi, "On the Alexander polynomial of the alternating knot" Osaka J. Math. , 10 (1958) pp. 181–189
[2]	R.H. Crowell, "Genus of alternating link types" Ann. of Math. (2) , 69 (1959) pp. 258–275
[3]	K. Murasugi, "On alternating knots" Osaka J. Math. , 12 (1960) pp. 277–303

Comments

A Seifert surface for a knot or link 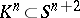is a connected, bicollared compact manifold 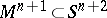such that 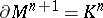. A subset 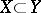is bicollared (in 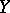) if there exists an imbedding 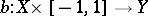such that 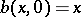for all 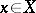. The mapping 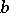or its image is the bicollar itself.

References

[a1]	D. Rolfsen, "Knots and links" , Publish or Perish (1976)