Ring with divided powers
Let $ R $
be a commutative ring with unit, and let $ A $
be an augmented $ R $-
algebra, i.e. there is given a homomorphism of $ R $-
algebras $ \epsilon : A \rightarrow R $.
A divided power structure on $ R $(
or, more precisely, on the augmentation ideal $ I( A)= \mathop{\rm Ker} ( \epsilon ) $)
is a sequence of mappings
$$ \gamma _ {r} : I( A) \rightarrow I( A),\ r = 1, 2 \dots $$
such that
1) $ \gamma _ {1} ( x) = x $;
2) $ \gamma _ {r} ( x) \gamma _ {s} ( x) = ( {} _ { s } ^ {r+ s } ) \gamma _ {r+} s ( x) $;
3) $ \gamma _ {t} ( x+ y)= \sum _ {r=} 0 ^ {t} \gamma _ {r} ( x) \gamma _ {t-} r ( y) $;
4) $ \gamma _ {s} ( \gamma _ {r} ( x))= \epsilon _ {s,r} \gamma _ {rs} ( x) $;
5) $ \gamma _ {r} ( xy) = r! \gamma _ {r} ( x) \gamma _ {r} ( y) $;
where $ \gamma _ {0} ( x) = 1 $ in 3) and
$$ \epsilon _ {s,r} = \left ( \begin{array}{c} r \\ r- 1 \end{array} \right ) \left ( \begin{array}{c} 2r \\ r- 1 \end{array} \right ) \dots \left ( \begin{array}{c} ( s- 1) r \\ r- 1 \end{array} \right ) . $$
In case $ A $ is a graded commutative algebra over $ R $ with $ A _ {0} = R $, these requirements are augmented as follows (and changed slightly):
6) $ \gamma _ {r} ( A _ {k} ) \subset A _ {rk} $,
with 5) replaced by
5')
$$ \begin{array}{ll} \gamma _ {r} ( xy) = r! \gamma _ {r} ( x) \gamma _ {r} ( y) & \textrm{ for } r\geq 2 \textrm{ and } x, y \textrm{ of even degree } ; \\ \gamma _ {r} ( xy) = 0 & \textrm{ for } r\geq 2 \textrm{ and } x, y \textrm{ of odd degree } . \\ \end{array} $$
Given an $ R $- module $ M $, an algebra with divided powers $ \Gamma ( M) $ is constructed as follows. It is generated (as an $ R $- algebra) by symbols $ m ^ {(} r) $, $ m \in M $, $ r= 1, 2 \dots $ and between these symbols the following relations are imposed:
$$ ( m _ {1} + m _ {2} ) ^ {(} t) = \sum _ { r= } 0 ^ { t } m _ {1} ^ {(} r) m _ {2} ^ {(} t- r) , $$
$$ ( \alpha m ) ^ {(} t) = \alpha ^ {t} m ^ {(} t) ,\ \alpha \in R, $$
$$ m ^ {(} r) m ^ {(} s) = \left ( \begin{array}{c} r+ s \\ r \end{array} \right ) m ^ {(} r+ s) . $$
This $ \Gamma ( M) $ satisfies 1)–5). The augmentation sends $ m ^ {(} r) $ to $ 0 $( $ r> 0 $). If one assigns to $ m ^ {(} r) $ the degree $ 2r $, a graded commutative algebra is obtained with $ \Gamma ( M) _ {0} = R $, $ \Gamma ( M) _ {1} = M $ which satisfies 1)–4), 5'), 6).
If $ A $ is a $ \mathbf Q $- algebra, divided powers can always be defined as $ a \mapsto ( r!) ^ {-} 1 a ^ {r} $. The relations 1)–5) can be understood as a way of writing down the interrelations between such "divided powers" (such as the one resulting from the binomial theorem) without having to use division by integers.
A divided power sequence in a co-algebra $ ( C, \mu ) $ is a sequence of elements $ y _ {0} = 1 , y _ {1} , y _ {2} \dots $ satisfying
$$ \mu ( y _ {n} ) = \sum _ {i+ j= n } y _ {i} \oplus y _ {j} . $$
Divided power sequences are used in the theories of Hopf algebras and formal groups (cf. Formal group; Hopf algebra), [a1]–[a3]. Rings with divided powers occur in algebraic topology (where they provide a natural setting for power cohomology operations), [a4], [a5], and the theory of formal groups [a3], [a2].
References
| [a1] | N. Roby, "Les algèbres à puissances divisées" Bull. Soc. Math. France , 89 (1965) pp. 75–91 |
| [a2] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) |
| [a3] | P. Cartier, "Exemples d'hyperalgèbres" , Sem. S. Lie 1955/56 , 3 , Secr. Math. Univ. Paris (1957) |
| [a4] | E. Thomas, "The generalized Pontryagin cohomology operations and rings with divided powers" , Amer. Math. Soc. (1957) |
| [a5] | S. Eilenberg, S. MacLane, "On the groups 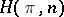 , II" Ann. of Math. , 60 (1954) pp. 49–189 , II" Ann. of Math. , 60 (1954) pp. 49–189 |
Ring with divided powers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ring_with_divided_powers&oldid=49407