Linear summation method
A summation method (cf. Summation methods) having the properties of linearity:
1) if the series $\sum_{k=0}^\infty a_k$ is summable by the summation method to the sum $A$, then the series $\sum_{k=0}^\infty ca_k$ is summable by this method to the sum $cA$;
2) if the series $\sum_{k=0}^\infty a_k$, $\sum_{k=0}^\infty b_k$ are summable by the summation method to $A$ and $B$ respectively, then the series $\sum_{k=0}^\infty(a_k+b_k)$ is summable by this method to the sum $A+B$.
All most widespread summation methods are linear; in particular, a matrix summation method and a semi-continuous summation method. There are non-linear summation methods. For example, the method in which summability of a series to the sum $S$ is defined by the existence of the limit $S$ of the sequence $\{T_n\}$, where
$$T_n=\frac{s_{n+1}s_{n-1}-s_n^2}{s_{n+1}+s_{n-1}-2s_n}$$
(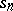 are the partial sums of the series), is not linear.
are the partial sums of the series), is not linear.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.F. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Linear summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_summation_method&oldid=33355