Boundary correspondence, principle of
A principle formulated in the following way. One says that the principle of boundary correspondence holds for a mapping $ f $
if the facts that $ f $
is a continuous mapping of the closure $ \overline{G}\; $
of a domain $ G $
onto the closure $ \overline{D}\; $
of a domain $ D $
and $ f $
is a homeomorphism of $ \overline{G}\; \setminus G $
onto $ \overline{D}\; \setminus D $
imply that $ f $
is a topological mapping of $ \overline{G}\; $
onto $ \overline{D}\; $.
Thus, the principle of boundary correspondence is in some sense converse to the boundary-correspondence principle (cf. Boundary correspondence (under conformal mapping)).
If $ G $ and $ D $ are plane domains with Euclidean boundaries homeomorphic to a circle and $ D $ is bounded, then the principle of boundary correspondence holds for analytic functions $ f $ on $ G $, i.e. $ f $ is a conformal mapping of $ G $ onto $ D $. In addition to that given above, various other forms of the principle of boundary correspondence are commonly used for conformal mappings (see [1]). The principle of boundary correspondence has been verified for orientable mappings in Euclidean space (see [2]).
References
| [1] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "On differentiable mappings" Dokl. Akad. Nauk SSSR , 95 : 5 (1954) pp. 921–923 (In Russian) |
| [3] | S.I. Pinchuk, "Holomorphic equivalence of certain classes of domains in 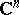 " Math. USSR-Sb. , 111 (153) : 1 (180) pp. 67–94; 159 Mat. Sb. , 111 (153) : 1 (1980) pp. 67–94; 159 " Math. USSR-Sb. , 111 (153) : 1 (180) pp. 67–94; 159 Mat. Sb. , 111 (153) : 1 (1980) pp. 67–94; 159 |
Boundary correspondence, principle of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_correspondence,_principle_of&oldid=18233