Bredon cohomology
An ordinary equivariant cohomology for a finite group $ G $,
defined in [a1], on the category $ G $-
CW of $ G $-
complexes (cf. Complex; CW-complex). The objects of $ G $-
CW are the CW-complexes $ X $
with a cellular action of $ G $,
satisfying the condition that, for every subgroup $ H $
of $ G $,
the fixed point set $ X ^ {H} $
is a subcomplex of $ X $.
The morphisms are the cellular $ G $-
mappings. Let $ O _ {G} $
be the full subcategory of $ G $-
CW whose objects are the $ G $-
orbits $ G/H $,
where $ H $
is a subgroup of $ G $.
For every contravariant functor $ M $
from $ O _ {G} $
to the category $ { \mathop{\rm Ab} } $
of Abelian groups, there exists a Bredon cohomology theory $ \{ H ^ {n} _ {G} ( -,M ) \} _ {n \in \mathbf N } $
which, after restriction to $ O _ {G} $,
vanishes for $ n > 0 $
and is equal to $ M $
for $ n = 0 $.
Let $ c _ {*} ( X ) $ be the chain complex of functors from $ O _ {G} $ to $ { \mathop{\rm Ab} } $ such that, for every subgroup $ H $ of $ G $, $ c _ {*} ( X ) ( G/H ) = C _ {*} ( X ^ {H} ) $ is the ordinary cellular chain complex of $ X ^ {H} $. Then
$$ H ^ {n} _ {G} ( X,M ) = H ^ {n} ( { \mathop{\rm Hom} } _ {O _ {G} } ( c _ {*} ( X ) ,M ) ) , $$
where $ { \mathop{\rm Hom} } _ {O _ {G} } ( -, - ) $ denotes the set of natural transformations of functors. The functors $ c _ {n} ( X ) $ are projective objects in the category of coefficient systems and there is a spectral sequence
$$ { \mathop{\rm Ext} } ^ {p} _ {O _ {G} } ( h _ {q} ( X ) ,M ) \Rightarrow H ^ {p + q } _ {G} ( X,M ) , $$
where $ h _ {q} ( X ) ( G/H ) = H _ {q} ( X ^ {H} ) $.
Let $ Y $ be a $ G $- space with base point $ y _ {0} $( cf., e.g., Equivariant cohomology). Important examples of coefficient systems are the homotopy group functors $ \pi _ {n} ( Y ) $ defined by $ \pi _ {n} ( Y ) ( G/H ) = \pi _ {n} ( Y ^ {H} ,y _ {0} ) $. The obstruction theory for $ G $- mappings $ f : X \rightarrow Y $ is formulated in terms of the cohomology groups $ H ^ {n} _ {G} ( X, \pi _ {m} ( Y ) ) $. For any coefficient system $ M $ and natural number $ n > 0 $, there is a pointed Eilenberg–MacLane $ G $- complex $ K ( M,n ) $ such that $ \pi _ {n} ( K ( M,n ) ) = M $ and $ \pi _ {m} ( K ( M,n ) ) $ vanishes whenever $ n \neq m $. For every $ G $- complex $ X $, $ H ^ {n} _ {G} ( X,M ) = [ X,K ( M,n ) ] _ {G} $, where $ [ -, - ] _ {G} $ denotes $ G $- homotopy classes of $ G $- mappings.
If $ h ^ {*} _ {G} ( - ) $ is an equivariant cohomology theory defined on the category $ G $- CW, then there exists an Atiyah–Hirzebruch-type spectral sequence
$$ H ^ {p} _ {G} ( X,h ^ {q} ) \rightarrow h ^ {p + q } _ {G} ( X ) , $$
where $ h ^ {q} $ is the restriction of $ h ^ {q} _ {G} ( - ) $ to $ O _ {G} $. Bredon cohomology for an arbitrary topological group is studied in [a4] and [a5]. Singular ordinary equivariant cohomology is defined in [a2] (the finite case) and in [a3]. If a coefficient system $ M $ is a Mackey functor, then the Bredon cohomology $ H ^ {*} _ {G} ( -,M ) $ can be extended to an ordinary $ { \mathop{\rm RO} } ( G ) $- graded cohomology [a6].
References
| [a1] | G.E. Bredon, "Equivariant cohomology theories" , Lecture Notes in Mathematics , 34 , Springer (1967) |
| [a2] | T. Bröcker, "Singuläre Definition der äquivarianten Bredon Homologie" Manuscr. Math. , 5 (1971) pp. 91–102 |
| [a3] | S. Illman, "Equivariant singular homology and cohomology" , Memoirs , 156 , Amer. Math. Soc. (1975) |
| [a4] | T. Matumoto, "Equivariant cohomology theories on 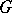 -CW-complexes" Osaka J. Math. , 10 (1973) pp. 51–68 -CW-complexes" Osaka J. Math. , 10 (1973) pp. 51–68 |
| [a5] | S.J. Wilson, "Equivariant homology theories on 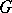 -complexes" Trans. Amer. Math. Soc. , 212 (1975) pp. 155–171 -complexes" Trans. Amer. Math. Soc. , 212 (1975) pp. 155–171 |
| [a6] | L.G. Lewis, J.P. May, J. McClure, "Ordinary RO(G)-graded cohomology" Bull. Amer. Math. Soc. , 4 (1981) pp. 208–212 |
Bredon cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bredon_cohomology&oldid=16015