Quasi-triangular Hopf algebra

dual quasi-triangular Hopf algebra, co-quasi-triangular Hopf algebra, quantum group

A quantum group in the strict sense, i.e. a Hopf algebra $H$ equipped with a further (co-) quasi-triangular structure $\mathcal{R}$ obeying certain axioms such that the category of (co-) modules of $H$ is a braided category (cf. also Quantum groups). This is arguably the key property behind the quantum group enveloping algebras $U _ { q } ( \mathfrak { g } )$ or their associated quantum group coordinate rings $G_q$.

More precisely, a quasi-triangular Hopf algebra is $( H , \mathcal{R} )$ where $H$ is a Hopf algebra over a field $k$ and $\mathcal{R} \in H \otimes H$ obeys

\begin{equation*} \tau \circ \Delta h = \mathcal{R} ( \Delta h ) \mathcal{R} ^ { - 1 } , \forall h \in H, \end{equation*}

\begin{equation*} ( \Delta \bigotimes \text { id } ) {\cal R} = {\cal R} _ { 13 } {\cal R} _ { 23 } , ( \text { id } \bigotimes \Delta ) {\cal R} = {\cal R} _ { 13 } {\cal R} _ { 12 }, \end{equation*}

where $\tau$ is the permutation operation on $H ^ { \otimes 2 }$ and $\mathcal{R} _ { 12 } \equiv \mathcal{R} \otimes 1$, $\mathcal{R} _ { 23 } = 1 \otimes \mathcal{R}$ are in $H ^ { \otimes 3 }$ in the latter equations. One may show that $\mathcal{R}$ then obeys

\begin{equation*} \mathcal{R} _ { 12 } \mathcal{R} _ { 13 } \mathcal{R} _ { 23 } = \mathcal{R} _ { 23 } \mathcal{R} _ { 13 } \mathcal{R} _ { 12 }, \end{equation*}

which is an abstract form of the Yang–Baxter equation. One denotes the Hopf algebra structure by $\Delta$ for the co-product, and denotes by the co-unit and by $S$ the antipode.

Examples.

1) When $q \in k$ is an $n$th root of $1$, the quantum group $\mathbf{Z} _ { q , n }$ is given by the polynomial algebra $k [ g ]$ modulo $g ^ { n } = 1$ (the group ring of $\mathbf{Z} / n \mathbf{Z}$) with co-algebra, antipode and quasi-triangular structure

\begin{equation*} \Delta g = g \bigotimes g , \epsilon g = 1 , S g = g ^ { - 1 } = g ^ { n - 1 }, \end{equation*}

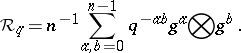It is assumed that $n$ is invertible in $k$.

2) When $q$ is a primitive $n$th root of $1$, the finite-dimensional quantum group $u _ { q } ( \operatorname{sl} _ { 2 } )$ is the free associative algebra $k ( E , F , g , g ^ { - 1 } )$ modulo the relations

\begin{equation*} g ^ { n } = 1 , E ^ { n } = F ^ { n } = 0, \end{equation*}

\begin{equation*} g E g ^ { - 1 } = q ^ { 2 } E , g F g ^ { - 1 } = q ^ { - 2 } F , [ E , F ] = \frac { g - g ^ { - 1 } } { q - q ^ { - 1 } } \end{equation*}

and the co-algebra, antipode and quasi-triangular structure

\begin{equation*} \Delta g = g \bigotimes g,\; \epsilon g = 1,\; \ S _ { g } = g ^ { - 1 }, \end{equation*}

\begin{equation*} \Delta E = E \bigotimes g + 1 \bigotimes E , \epsilon E = 0 , S E = - E g ^ { - 1 } , \Delta F = F \bigotimes 1 + g ^ { - 1 } \bigotimes F , \epsilon F = 0 , S F = - g F, \end{equation*}

\begin{equation*} \mathcal{R} = \mathcal{R} _ { q ^ { 2 } } e _ { q ^ { - 2 } } ^ { ( q - q ^ { - 1 } ) E \bigotimes F }, \end{equation*}

where

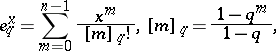is the $q$-exponential with $q$-integers $[ m ]_{ q}$ in the factorial.

For general $q \in k ^ { * }$ (an invertible element of $k$), one has the infinite-dimensional Hopf algebra $U _ { q } ( \operatorname{sl} _ { 2 } )$, where the $g ^ { n } , E ^ { n } , F ^ { n }$ relations above are omitted. In this case $\mathcal{R}$ has to be described via some form of completion. One formulation is to work over the ring of formal power series ${\bf C} [ [ \hbar ] ]$ rather than over a field as above. If it is assumed that $q = e ^ { \hbar / 2 }$ and $g = q ^ { H }$, one can reformulate $U _ { q } ( \operatorname{sl} _ { 2 } )$ with $H$ as a generator and define $\mathcal{R}$ with $q ^ { H \otimes H / 2 }$ in place of ${\cal R }_ { q ^ { 2 } }$ above (and now take an infinite sum in the exponential). It does not, however, live in the algebraic tensor product but in a completion of it. On the other hand, this formulation allows one to consider the structure to lowest order in $\hbar$. This is the Lie algebra $\operatorname{sl} _ { 2 }$, the Lie co-bracket $\delta : \operatorname{sl}_ { 2 } \rightarrow \operatorname{sl} _ { 2 } \otimes sl _ { 2 }$ (forming a Lie bi-algebra) and a Lie quasi-triangular structure $r \in \operatorname { sl} _ { 2 } \otimes \operatorname { sl} _ { 2 }$ obeying the classical Yang–Baxter equations. It extends to a Poisson bracket (cf. Poisson brackets) on the group $\operatorname{SL} _ { 2 }$, making it a Poisson Lie group. This means a Poisson bracket on the group such that the product mapping is a Poisson mapping from the direct product Poisson structure. There are similar quantum group enveloping algebras $u _ { q } ( \mathfrak { g } )$ and $U _ { q } ( \mathfrak { g } )$ for all complex semi-simple Lie algebras $\frak g$.

3) Every finite-dimensional Hopf algebra $H$ with invertible antipode can be "doubled" to obtain a quasi-triangular Hopf algebra $D ( H )$, called the quantum double of $H$. This contains $H$ and $H ^ { * \operatorname{op} }$ (the dual of $H$ with reversed product) as sub-Hopf algebras and the additional cross relations

\begin{equation*} \phi h = \sum h _{( 2 )} \phi_{ ( 2 )} \langle S h _ { ( 1 ) } , \phi _ { ( 1 ) } \rangle \langle h _ { ( 3 ) } , \phi _ { ( 3 ) } \rangle \end{equation*}

for all $h \in H$ and $\phi \in H ^ { * }$, where $\Delta h = \sum h_{ ( 1 )} \otimes h_{ ( 2 )}$ is a notation for the co-product of $H$, etc., and $\langle \, .\, ,\, . \, \rangle$ denotes the evaluation pairing. The quasi-triangular structure is

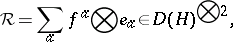where $\{ e _ { a } \}$ is a basis of $H$ and $\{ f ^ { a } \}$ is a dual basis. $D ( H )$ can in fact be built explicitly on the vector space $H ^ { * } \otimes H$ as a double cross product 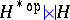. The braided category of $D ( H )$-modules can be identified with that of crossed $H$-modules $\square _ { H } ^ { H } \mathcal{M}$ by viewing a co-action of $H$ as an action of $H ^ { * \operatorname{op} }$ by evaluation.

Dually, i.e. reversing all arrows, one has the notion of a dual quasi-triangular or co-quasi-triangular Hopf algebra $( H , \mathcal{R} )$ where $H$ is a Hopf algebra and $\mathcal{R} : H \otimes H \rightarrow k $ obeys

\begin{equation*} \sum g _{( 1 )} h _ { ( 1 ) } \mathcal{R} ( h _ { ( 2 ) } \bigotimes g _ { ( 2 ) } ) = \sum \mathcal{R }( h _ { ( 1 ) } \bigotimes g _ { ( 1 ) } ) h _ { ( 2 ) } g_{ ( 2 )}, \end{equation*}

\begin{equation*} \mathcal{R}(hg\bigotimes f ) = \sum \mathcal{R} ( h \bigotimes f _ { ( 1 ) } ) \mathcal{R} ( g \bigotimes f_{ ( 2 )} ) , \mathcal{R} ( h \bigotimes g \,f ) = \sum \mathcal{R}(h_{(1)} \bigotimes f) \mathcal{R}(h_{(2)} \bigotimes g), \end{equation*}

for $h , g , f \in H$. One also requires $\mathcal{R}$ to be convolution-invertible in the sense

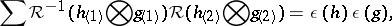for $h , g \in H$.

A) Let $G$ be an Abelian group equipped with a bi-character $\beta : G \times G \rightarrow k ^ { * }$ (a function multiplicative in each input). The group algebra $k G$ is the vector space with basis $G$ and with product among basis elements the group product. The co-product $\Delta g = g \otimes g$ and co-unit $\epsilon g = 1$ extended linearly make $k G$ into a Hopf algebra. The bi-character makes this dual quasi-triangular, with $\mathcal{R} = \beta$ on basis elements, extended linearly.

B) The dual quasi-triangular Hopf algebra $\operatorname{SL} _ { q } ( 2 )$ is the free associative algebra $k \langle a , b , c , d \rangle $ modulo the relations

\begin{equation*} c a = q a c ,\; b a = q a b ,\; d b = q b d ,\; d c = q c b, \end{equation*}

\begin{equation*} b c = c b , d a - a d = ( q - q ^ { - 1 } ) b c, \end{equation*}

and the "q-determinant relation"

\begin{equation*} a d - q ^ { - 1 } b c = 1. \end{equation*}

The co-algebra has the matrix form

\begin{equation*} \Delta \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) = \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) \bigotimes \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right), \end{equation*}

\begin{equation*} \epsilon \left( \begin{array} { l l } { a } & { b } \\ { c } & { d } \end{array} \right) = \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \end{equation*}

(matrix multiplication understood). The antipode is

\begin{equation*} S d = a , S a = d , S b = - q b , S c = - q ^ { - 1 } c \end{equation*}

and the dual quasi-triangular structure is

\begin{equation*} \mathcal{R} = q ^ { - 1 / 2 } \left( \begin{array} { c c c c } { q } & { 0 } & { 0 } & { 1 } \\ { 0 } & { 0 } & { q - q ^ { - 1 } } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 0 } & { q } \end{array} \right) \end{equation*}

on a basis $\{ a , b , c , d \}$ of generators. The extension to products is then determined. Here it is assumed that $q$ has a square root in $k$. The quantum group $\operatorname {GL} _ { q } ( 2 )$ is similar, with $a d - q ^ { - 1 } b c$ inverted rather than set to $1$.

There are similar quantum group coordinate rings $G_q$ for the standard families of simple Lie groups, known explicitly for the non-exceptional families. They are deformations of the classical coordinate rings and in fact quantize the Poisson Lie group structures on $G$ corresponding to $U _ { q } ( \mathfrak { g } )$. They are dually paired as Hopf algebras with $U _ { q } ( \mathfrak { g } )$.

C) More generally, given any invertible matrix solution $R$ of the Yang–Baxter equations, there is a dual-quasi-triangular bi-algebra of quantum matrices $A ( R )$ as the free associative algebra $k \langle t ^ { i } \square_j \rangle$ (on a matrix of generators) modulo the relations

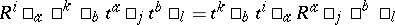(summation of repeated indices). The co-algebra has the matrix form

\begin{equation*} \Delta t ^ { i } \square_{ j} = t ^ { i } \square _ { a } \bigotimes t ^ { a } \square_{ j} ,\, \epsilon t ^ { i } \square _j = \delta ^ { i } \square_ j \end{equation*}

(summation over $a$). The dual-quasi-triangular structure is

\begin{equation*} \mathcal{R} ( t ^ { i } \square_{j} \bigotimes t ^ { k } \square_{l} ) = \mathbf{R} ^ { i } \square_ j \square ^ { k } \square_{l} , \end{equation*}

extended to products by the quasi-triangularity axioms. Note that $R$ need not obey the Yang–Baxter equations in order to have a bi-algebra: $R$ provides the dual quasi-triangular structure.

In between these formulations is an intermediate one, called a quasi-triangular dual pair. This is a pair of Hopf algebras $H , A$, a duality pairing $\langle \cdot , \cdot \rangle : A \otimes H \rightarrow k $ between them, and a mapping $\mathcal{R} : A \rightarrow H$ obeying certain axioms. In particular, $G _ { q } , U _ { q } ( \mathfrak { g } )$ are dually paired and there is a suitable mapping ${\cal R} : G _ { q } \rightarrow U _ { q } ( {\frak g} )$. This provides a way of working with quasi-triangular structures that includes quantum group enveloping algebras but avoids formal power series.

References

[a1]	V.G. Drinfel'd, "Quantum groups" A. Gleason (ed.) , Proc. Internat. Math. Congress , Amer. Math. Soc. (1987) pp. 798–820
[a2]	L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtajan, "Quantization of Lie groups and Lie algebras" Leningrad Math. J. , 1 (1990) pp. 193–225
[a3]	S. Majid, "Quasitriangular Hopf algebras and Yang-Baxter equations" Internat. J. Modern Physics A , 5 : 1 (1990) pp. 1–91
[a4]	S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995)