Luzin criterion
for measurability of a function of a real variable
For a function  , defined on the interval
, defined on the interval  and almost-everywhere finite, to be measurable it is necessary and sufficient that for any
and almost-everywhere finite, to be measurable it is necessary and sufficient that for any  there is a function
there is a function  , continuous on
, continuous on 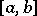 , such that the measure of the set
, such that the measure of the set
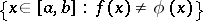 |
is less than  . It was proved by N.N. Luzin [1]. In other words, an almost-everywhere finite function is measurable if and only if it becomes continuous if one neglects a set of arbitrary small measure.
. It was proved by N.N. Luzin [1]. In other words, an almost-everywhere finite function is measurable if and only if it becomes continuous if one neglects a set of arbitrary small measure.
References
| [1] | N.N. [N.N. Luzin] Lusin, "Sur les propriétés des fonctions mesurables" C.R. Acad. Sci. Paris , 154 (1912) pp. 1688–1690 Zbl 43.0484.04 |
| [2] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) MR0640867 MR0354979 MR0148805 MR0067952 MR0039790 |
Comments
In the West, Luzin's criterion is known as Luzin's theorem (in spite of an ambiguity — cf. Luzin theorem) and is generally stated a little bit differently, more like in Luzin 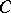 -property (but with a compact set instead of a perfect set). The tightness of the measure and the normality of the space makes all these formulations equivalent.
-property (but with a compact set instead of a perfect set). The tightness of the measure and the normality of the space makes all these formulations equivalent.
The Luzin criterion remains true if the interval 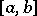 is replaced by any completely-regular space and the (restriction of the) Lebesgue measure by any tight bounded measure on the Borel
is replaced by any completely-regular space and the (restriction of the) Lebesgue measure by any tight bounded measure on the Borel 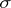 -field. In this general setting the Luzin property may be used in order to give an alternative definition of the notion of measurability (cf. [a1]) or, in recent works, a more adequate definition of this notion when
-field. In this general setting the Luzin property may be used in order to give an alternative definition of the notion of measurability (cf. [a1]) or, in recent works, a more adequate definition of this notion when 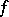 is no longer a real-valued function but, for example, a Banach-valued function.
is no longer a real-valued function but, for example, a Banach-valued function.
The Luzin criterion is intimately related to the Egorov theorem and to the notion of measurability according to Carathéodory (cf. Carathéodory measure).
References
| [a1] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) MR0583191 Zbl 1116.28002 Zbl 1106.46005 Zbl 1106.46006 Zbl 1182.28002 Zbl 1182.28001 Zbl 1095.28002 Zbl 1095.28001 Zbl 0156.06001 |
| [a2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [a3] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1966) pp. 98 MR0210528 Zbl 0142.01701 |
| [a4] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202 |
Luzin criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Luzin_criterion&oldid=15197