Hopf ring
A (graded) ring object in the category of (graded) co-commutative co-algebras (cf. Co-algebra). Such an object consists, first, of a sequence $ \{ H _ {i} \} $
of Abelian group objects in the category. These are better known as commutative Hopf algebras with conjugation. Since they belong to the category, they have a coproduct:
$$ \psi : {H _ {i} } \rightarrow {H _ {i} \otimes H _ {i} } . $$
Let $ \psi ( x ) = \sum x ^ \prime \otimes x ^ {\prime \prime } $. As group objects in a category of co-algebras, the $ H _ {i} $ also have a product $ H _ {i} \otimes H _ {i} \rightarrow H _ {i} $. Below, this product is denoted by $ * $. The "*" product should be thought of as "addition" in the ring as it is the pairing which gives the Abelian group structure. For ring "multiplication" one has
$$ \circ : {H _ {i} \otimes H _ {j} } \rightarrow {H _ {i + j } } . $$
As with any ring, there must be a distributive law relating the multiplication and the addition. Chasing diagrams in the category one sees that it is:
$$ x \circ ( y * z ) = \sum \pm ( x ^ \prime \circ y ) * ( x ^ \prime \circ z ) . $$
Hopf rings arise naturally in the study of the $ \Omega $- spectra associated with generalized cohomology theories. Any generalized cohomology theory, $ G ^ {*} ( X ) $, gives rise to a sequence of spaces, $ \{ {\underline{G} } _ {k} \} $, with the property that $ G ^ {k} ( X ) \simeq [ X, {\underline{G} } _ {k} ] $, the homotopy classes of mappings. If $ G $ is a multiplicative theory, then $ \{ {\underline{G} } _ {k} \} $ is a graded ring object in the homotopy category. If $ E $ represents a generalized homology theory and if there is a Künneth isomorphism for the $ E $- homology of the spaces in the $ \Omega $- spectra for $ G $, then the sequence $ \{ E _ {*} ( {\underline{G} } _ {*} ) \} $ becomes a Hopf ring. One can thus use knowledge of generalized homologies to further the understanding of generalized cohomologies by studying their classifying spaces using Hopf rings.
There are a number of Hopf rings which have been computed. Examples are $ E _ {*} ( {\underline{BP } } _ {*} ) $ and $ E _ {*} ( {\underline{MU } } _ {*} ) $, $ E $ a complex orientable theory, [a9] (the basic reference for Hopf rings); $ E _ {*} ( {\underline{K ( n ) } } _ {*} ) $ and $ E _ {*} ( {\underline{P ( n ) } } _ {*} ) $, $ E $ a complex orientable theory with $ I _ {n} = 0 $, [a14] and [a8]; $ H _ {*} ( K ( \mathbf Z/ {( p ) } , * ) ) $, [a13], § 8; $ K ( n ) _ {*} ( - ) $ for Eilenberg–MacLane spaces, [a10]; $ K ( n ) _ {*} ( {\underline{k ( n ) } } _ {\ * } ) $, [a5]; $ H _ {*} ( {\underline{KO } } ) $, [a11]; and the breakthrough description of $ H _ {*} ( QS ^ {0} , \mathbf Z/ ( 2 ) ) $ in [a12], and its sequel for $ H _ {*} ( QS ^ {*} , \mathbf Z/ ( 2 ) ) $ in [a1] followed by corresponding results for odd primes in [a7]. Other references are [a2], [a3], [a4], and [a6].
Hopf rings have a very rich algebraic structure, useful in two distinct ways: descriptive and computational. All of the above examples have their Hopf rings described with just a few generators and relations. The computations are generally carried out using Hopf ring techniques as well.
References
| [a1] | P.J. Eccles, P.R. Turner, W.S. Wilson, "On the Hopf ring for the sphere" Math. Z. , 224 (2) (1997) pp. 229–233 |
| [a2] | M.J. Hopkins, J.R. Hunton, "The structure of spaces representing a Landweber exact cohomology theory" Topology , 34 (1) (1995) pp. 29–36 |
| [a3] | J.R. Hunton, N. Ray, "A rational approach to Hopf rings" J. Pure Appl. Algebra , 101 (3) (1995) pp. 313–333 |
| [a4] | T. Kashiwabara, "Hopf rings and unstable operations" J. Pure Appl. Algebra , 194 (1994) pp. 183–193 |
| [a5] | R. Kramer, "The periodic Hopf ring of connective Morava 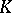 -theory" Ph.D. Thesis, Johns Hopkins Univ. (1990) -theory" Ph.D. Thesis, Johns Hopkins Univ. (1990) |
| [a6] | T. Kashiwabara, N.P. Strickland, P.R. Turner, "Morava 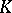 -theory Hopf ring for -theory Hopf ring for 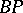 " C. Broto (ed.) etAAsal. (ed.) , Algebraic Topology: New Trends in Localization and Periodicity , Progress in Mathematics , 139 , Birkhäuser (1996) pp. 209–222 " C. Broto (ed.) etAAsal. (ed.) , Algebraic Topology: New Trends in Localization and Periodicity , Progress in Mathematics , 139 , Birkhäuser (1996) pp. 209–222 |
| [a7] | Y. Li, "On the Hopf ring for the sphere" Ph.D. Thesis, Johns Hopkins Univ. (1996) |
| [a8] | D.C. Ravenel, W.S. Wilson, "The Hopf ring for 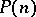 " Canadian J. Math. , 48 (5) (1996) pp. 1044–1063 " Canadian J. Math. , 48 (5) (1996) pp. 1044–1063 |
| [a9] | D.C. Ravenel, W.S. Wilson, "The Hopf ring for complex cobordism" J. Pure Appl. Algebra , 9 (1977) pp. 241–280 |
| [a10] | D.C. Ravenel, W.S. Wilson, "The Morava 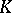 -theories of Eilenberg–Mac Lane spaces and the Conner–Floyd conjecture" Amer. J. Math. , 102 (1980) pp. 691–748 -theories of Eilenberg–Mac Lane spaces and the Conner–Floyd conjecture" Amer. J. Math. , 102 (1980) pp. 691–748 |
| [a11] | N. Strickland, "Bott periodicity and Hopf rings" Ph.D. Thesis, Univ. Manchester (1992) |
| [a12] | P.R. Turner, "Dickson coinvariants and the homology of 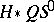 " Math. Z. , 224 (2) (1997) pp. 209–228 " Math. Z. , 224 (2) (1997) pp. 209–228 |
| [a13] | W.S. Wilson, "Brown–Peterson homology: an introduction and sampler" , CBMS , 48 , Amer. Math. Soc. (1982) |
| [a14] | W.S. Wilson, "The Hopf ring for Morava 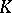 -theory" Publ. RIMS Kyoto Univ. , 20 (1984) pp. 1025–1036 -theory" Publ. RIMS Kyoto Univ. , 20 (1984) pp. 1025–1036 |
Hopf ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_ring&oldid=14158