Schur index

The Schur index of a central simple algebra $ A $ over a field $ K $( cf. Central simple algebra) is the degree of the division algebra $ D $ such that $ A $ is a full matrix algebra $ M _ {n} ( D) $ over $ D $.

Let $ G $ be a finite group, $ K $ a field and $ \overline{K}\; $ the algebraic closure of $ K $. Let $ V $ be an irreducible $ \overline{K}\; [ G] $- module with character $ \rho $( cf. Irreducible module). Let $ K( \rho ) $ be obtained from $ K $ by adjoining the values $ \rho ( g) $, $ g \in G $. The Schur index of the module $ V $, $ m _ {K} ( V) $, (or the Schur index of the character $ \rho $) is the minimal degree of a field $ S $ extending $ K( \rho ) $ such that $ V $ descends to $ S $, i.e. such that there is an $ S[ G] $- module $ W $ for which $ V \simeq \overline{K}\; \otimes _ {S} W $.

For a finite field $ K $ the Schur index is always $ 1 $, [a1].

A basic result on the Schur index is that for each $ K[ G] $- module $ W $ the multiplicity of $ V $ in $ \overline{K}\; \otimes _ {K} W $ is a multiple of $ m _ {K} ( V) $.

A field $ S \subset \overline{K}\; $ is a splitting field for a finite group $ G $ if each irreducible $ S[ G] $- module is absolutely irreducible, i.e. if $ \overline{K}\; \otimes _ {S} V $ is irreducible. The basic result on the Schur index quoted above readily leads to a proof of R. Brauer's result [a1] that if $ d $ is the exponent of a finite group $ G $( i.e. $ d $ is the smallest integer such that $ g ^ {d} = e $ for all $ g \in G $), then $ \mathbf Q ( 1 ^ {1/d} ) $ is a splitting field for $ G $.

The set $ S( K) $ of classes of central simple algebras over $ K $ which occur as components of a group algebra $ K[ G] $ for some finite group $ G $ is a subgroup of the Brauer group $ \mathop{\rm Br} ( K) $ of $ K $, and is known as the Schur subgroup of $ \mathop{\rm Br} ( K) $. Cf. [a4] for results on the structure of $ S( K) $.

References

[a1]	R. Brauer, "On the representation of a group of order in the field of 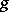-th roots of unity" Amer. J. Math. , 67 (1945) pp. 461–471
[a2]	C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. §90, §41
[a3]	B. Huppert, "Finite groups" , 2 , Springer (1982) pp. §1
[a4]	T. Yamada, "The Schur subgroup of the Brauer group" , Springer (1974)