Anti-de Sitter space

complete maximal space-like hypersurfaces in an

Let $ \mathbf R _ {p + 1 } ^ {n + p + 1 } $ be an $ ( n + p + 1 ) $- dimensional Minkowski space of index $ p + 1 $, i.e., $ \mathbf R _ {p + 1 } ^ {n + p + 1 } = \{ ( x _ {1} \dots x _ {n + p + 1 } ) \in \mathbf R ^ {n + p + 1 } \} $ and is equipped with the Lorentz metric $ \sum _ {i = 1 } ^ {n} ( dx _ {i} ) ^ {2} - \sum _ {j = 1 } ^ {p + 1 } ( dx _ {n + j } ) ^ {2} $. For $ c > 0 $, let

$$ H _ {p} ^ {n + p } ( c ) = \{ {x \in \mathbf R _ {p + 1 } ^ {n + p + 1 } } : $$

$$ \ {} {x _ {1} ^ {2} + \dots + x _ {n} ^ {2} - x _ {n + 1 } ^ {2} - \dots - x _ {n + p + 1 } ^ {2} = - {1 / c } } \} . $$

Thus, $ H _ {p} ^ {n + p } ( c ) $ is an $ ( n + p ) $- dimensional indefinite Riemannian manifold of index $ p $ and of constant curvature $ - c $. It is called an $ ( n + p ) $- dimensional anti-de Sitter space of constant curvature $ - c $ and of index $ p $. A hypersurface $ M $ of $ H _ {1} ^ {n + 1 } ( c ) $ is said to be space-like if the metric on $ M $ induced by that of ambient space $ H _ {1} ^ {n + 1 } ( c ) $ is positive definite. The mean curvature $ H $ of $ M $ is defined as in the case of Riemannian manifolds. By definition, $ M $ is a maximal hypersurface if the mean curvature $ H $ of $ M $ is identically zero. S. Ishihara proved that a complete maximal space-like hypersurface $ M $ in $ H _ {1} ^ {n + 1 } ( c ) $ satisfies $ S \leq nc $, and $ S = nc $ if and only if $ M $ is isometric to the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $, where $ S $ is the squared norm of the second fundamental form of $ M $ and $ H ^ {k} ( c _ {i} ) $, $ i = 1, 2 $, is a $ k $- dimensional hyperbolic space of constant curvature $ c _ {i} $. The rigidity of the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $ in $ H _ {1} ^ {n + 1 } ( c ) $ was proved by U.-H. Ki, H.S. Kim and H. Nakagawa [a3]: for a given integer $ n $ and constant $ c > 0 $, there exists a constant $ C < nc $, depending on $ n $ and $ c $, such that the hyperbolic cylinder $ H ^ {k} ( c _ {1} ) \times H ^ {n - k } ( c _ {2} ) $ is the only complete maximal space-like hypersurface in $ H _ {1} ^ {n + 1 } ( c ) $ of constant scalar curvature and such that $ S > C $. In particular, for $ n = 3 $, Q.M. Cheng [a1] has characterized the complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $ under the condition of constant Gauss–Kronecker curvature (cf. Gaussian curvature): Let $ M $ be a $ 3 $- dimensional complete maximal space-like hypersurface of $ H _ {1} ^ {4} ( c ) $. Now:

1) if the Gauss–Kronecker curvature of $ M $ is a non-zero constant, then $ M $ is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $;

2) if the scalar curvature $ K $ is constant and $ \inf K ^ {2} > 0 $, then $ M $ is the hyperbolic cylinder $ H ^ {1} ( c _ {1} ) \times H ^ {2} ( c _ {2} ) $. There are no complete maximal space-like hypersurfaces in $ H _ {1} ^ {4} ( c ) $ with constant scalar curvature and $ \sup K ^ {2} < { {S ^ {3} } / {54 } } $.

On the other hand, complete space-like submanifolds in anti-de Sitter spaces with parallel mean curvature have been investigated by many authors.

Cf. also De Sitter space.

References

[a1]	Q.M. Cheng, "Complete maximal space-like hypersurfaces of 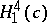" Manuscr. Math. , 82 (1994) pp. 149–160
[a2]	T. Ishikawa, "Maximal space-like submanifolds of a pseudo–Riemannian space of constant curvature" Michigan Math. J. , 35 (1988) pp. 345–352
[a3]	U-H. Ki, H.S. Kim, H. Nakagawa, "Complete maximal space-like hypersurfaces of an anti-de Sitter space" Kyungpook Math. J. , 31 (1991) pp. 131–141