Difference between revisions of "Real algebraic variety"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
(latex details) |
||
| Line 131: | Line 131: | ||
$$ | $$ | ||
| − | \prod _ {i = 1 } ^ { q } ( 1 + x _ {i} + \dots + x _ {i} ^ {m-} | + | \prod _ {i = 1 } ^ { q } ( 1 + x _ {i} + \dots + x _ {i} ^ {m-2} ) , |
$$ | $$ | ||
| Line 255: | Line 255: | ||
where $ \sigma ( \mathbf C A ) $ | where $ \sigma ( \mathbf C A ) $ | ||
| − | is the [[ | + | is the [[signature]] of the variety $ \mathbf C A $. |
B) For an $ ( M- 1) $- | B) For an $ ( M- 1) $- | ||
Latest revision as of 08:30, 14 January 2024
The set $ A = X ( \mathbf R ) $
of real points of an algebraic variety $ X $
defined over the field $ \mathbf R $
of real numbers. A real algebraic variety is said to be non-singular if $ X $
is non-singular. In such a case $ A $
is a smooth variety, and its dimension $ \mathop{\rm dim} A $
is equal to the dimension of the complex variety $ \mathbf C A = X ( \mathbf C ) $;
the latter is known as the complexification of the variety $ A $.
Non-singular regular complete intersections have been most thoroughly studied. These are varieties $ X $ in the projective space $ \mathbf R P ^ {q} $ which are non-singular regular intersections of hypersurfaces $ p _ {i} ( z) = 0 $, $ 1 \leq i \leq s $, where $ p _ {i} ( z) $ is a homogeneous real polynomial in $ q $ variables of degree $ m _ {i} $. In such a case the matrix
$$ \left \| \frac{\partial p _ {i} }{\partial z _ {j} } \right \| $$
has rank $ s $ at all points $ z \in \mathbf C A $; $ \mathop{\rm dim} A = n = q- s $.
Let $ B $ denote the real algebraic variety defined as the intersection system
$$ p _ {i} ( z) = 0 ,\ 1\leq i \leq s- 1,\ p( z) = p _ {s} ( z) \ \textrm{ and } \ \ m = m _ {s} . $$
Examples of regular complete intersections are:
1) A plane real algebraic curve; here $ q= 2 $, $ s= 1 $, $ \mathbf C B = \mathbf C P ^ {2} $, $ B = \mathbf R P ^ {2} $.
2) A real algebraic hypersurface; here $ s= 1 $, $ \mathbf C B = \mathbf C P ^ {q} $, $ B = \mathbf R P ^ {q} $. In particular, if $ q= 3 $, a real algebraic surface is obtained.
3) A real algebraic space curve; here $ q= 3 $, $ s= 2 $. The surface $ B $ is defined by an equation $ p _ {1} ( z) = 0 $, while the curve $ A $ is cut out on $ B $ by a surface $ p _ {2} ( z) = 0 $.
A real algebraic curve $ A $ of order $ m _ {1} $ in the plane $ \mathbf R P ^ {2} $ consists of finitely many components diffeomorphic to a circle. If $ m _ {1} $ is even, these components are all two-sidedly imbedded in $ \mathbf R P ^ {2} $; if $ m _ {1} $ is odd, one component is imbedded one-sidedly, while the remaining ones are imbedded two-sidedly. A two-sidedly imbedded component of $ A $ is called an oval of $ A $. An oval lying inside an odd number of other ovals of $ A $ is called odd, while the remaining ovals are even.
The number of components of a plane real algebraic curve of order $ m _ {1} $ is not larger than $ ( m _ {1} - 1 ) ( m _ {1} - 2 ) / 2 + 1 $( Harnack's theorem) [1]. For each $ m _ {1} $ there exists a plane real algebraic curve with this largest number of components — the $ M $- curve. (For methods of constructing $ M $- curves see [1], [2], [3]; for a generalization of these results to include space curves, see [2].)
D. Hilbert posed in 1900 the problem of studying the topology of real algebraic varieties, and also of the imbedding of real algebraic varieties into $ \mathbf R P ^ {q} $ and of one real algebraic variety into another (Hilbert's 16th problem). He also pointed out difficult partial problems: the study of the mutual locations of the ovals of a sixth-order curve, and the topology and the imbedding of a real algebraic fourth-order surface into $ \mathbf R P ^ {3} $. These partial problems have been solved [12], [13].
For a plane real algebraic curve $ A $ of even order $ m _ {1} $ the following exact inequality is valid:
$$ - \frac{1}{8} ( 3 m _ {1} ^ {2} - 6 m _ {1} ) \leq P - N \leq \frac{1}{8} ( 3 m _ {1} ^ {2} - 6 m _ {1} ) + 1 , $$
where $ P $ is the number of even ovals and $ N $ is the number of odd ovals of $ A $( Petrovskii's theorem). If $ m _ {1} $ is odd, a similar inequality is valid for $ A \cup L $, where $ L $ is a straight line in general position [4]. When these results are generalized to include the case of a real algebraic hypersurface of even order, the role of the difference $ P- N $ is played by the Euler characteristic $ \chi ( B _ {+} ) $, where $ B _ {+} = \{ {z \in B } : {p( z) \geq 0 } \} $, while if $ q $ is odd, the role of $ P- N $ is played by $ \chi ( A) $. Thus, for a real algebraic hypersurface $ A $ of even order $ m _ {1} $,
$$ | \chi ( B _ {+} ) | \leq \frac{( m _ {1} - 1) ^ {q} }{2} - s( q; m _ {1} ) + \frac{1}{2} , $$
where $ s ( q ; m _ {1)} $ is the number of terms of the polynomial
$$ \prod _ {i = 1 } ^ { q } ( 1 + x _ {i} + \dots + x _ {i} ^ {m-2} ) , $$
of degree not higher than $ ( qm _ {1} - 2q - m _ {1} ) / 2 $; if $ q $ is odd, then for any $ m _ {1} $,
$$ | \chi ( A) | \leq ( m _ {1} - 1 ) ^ {q} - 2s ( q ; m _ {1} ) + 1 , $$
[5]. The following inequality is satisfied for a real algebraic space curve (in $ \mathbf R P ^ {3} $) for even $ m _ {1} $:
$$ | \chi ( B _ {+} ) | \leq \frac{1}{3} m _ {1} ^ {3} + \frac{3}{8} m _ {1} m _ {2} ^ {2} + \frac{1}{4} m _ {1} ^ {2} m _ {2} + $$
$$ - m _ {1} ^ {2} - m _ {1} m _ {2} + \frac{7}{6} m _ {1} + \frac{| \chi ( B) | }{2} $$
(if $ m _ {1} = 2 $, this estimate is exact [6]). Petrovskii's theorem has been generalized to arbitrary real algebraic varieties .
For a plane real algebraic $ M $- curve of even order $ m _ {1} $ the following congruence is valid:
$$ P - N \equiv \left ( \frac{m _ {1} }{2} \right ) ^ {2} \mathop{\rm mod} 8 , $$
[8], , [13]. In proving this congruence ([8], ), real algebraic varieties were studied by methods of differential topology in a form which opened the way for further investigations. Let the plane real algebraic curve $ A $ have even order $ m = 2k $ and let the sign of $ p( z) $ be chosen so that $ B _ {+} $ is orientable, while $ P _ {+} , P _ {0} , P _ {-} $ denote, respectively, the number of ovals of $ A $ which externally bound the components of the set $ B _ {+} $ with positive, zero and negative Euler characteristics. In a similar manner, $ N _ {+} , N _ {0} , N _ {-} $ are the numbers of such odd ovals for $ B _ {-} = \{ {z \in B } : {p( z) \leq 0 } \} $. Then [8], [3],
$$ P _ {-} + P _ {0} \leq \frac{1}{2} ( k - 1 ) ( k - 2 ) + E ( k) , $$
$$ N _ {-} + N _ {0} \leq \frac{1}{2} ( k - 1 ) ( k - 2 ) , $$
$$ P _ {-} \geq N - \frac{3}{2} k ( k - 1 ) , $$
$$ N _ {-} \geq P - \frac{3}{2} k ( k - 1 ) , $$
where
$$ E ( k) = \frac{1}{2} ( 1 + ( - 1 ) ^ {k} ) . $$
For an arbitrary real algebraic variety in a $ q $- dimensional projective space the following inequality is valid:
$$ \mathop{\rm dim} H _ {*} ( A ; \mathbf Z _ {2} ) \leq \mathop{\rm dim} H _ {*} ( \mathbf C A ; \mathbf Z _ {2} ) , $$
where $ H _ {*} ( A; \mathbf Z _ {2} ) = \sum H _ {i} ( A; \mathbf Z _ {2} ) $ is the homology space of the variety $ A $ with coefficients in $ \mathbf Z _ {2} $. This inequality is a generalization of Harnack's theorem. If
$$ \mathop{\rm dim} H _ {*} ( \mathbf C A ; \mathbf Z _ {2} ) - \mathop{\rm dim} H _ {*} ( A ; \mathbf Z _ {2} ) = 2t, $$
where $ t $ is always an integer, $ A $ is said to be an $ ( M- t) $- variety. If $ t= 0 $, $ A $ is an $ M $- variety.
The validity of the following congruences has been demonstrated:
A) For an $ M $- variety $ A $ and for even $ n $:
$$ \chi ( A ) \equiv \sigma ( \mathbf C A ) \mathop{\rm mod} 16 , $$
where $ \sigma ( \mathbf C A ) $ is the signature of the variety $ \mathbf C A $.
B) For an $ ( M- 1) $- variety $ A $ and even $ n $([13]):
$$ \chi ( A ) \equiv \sigma ( \mathbf C A ) \pm 2 \mathop{\rm mod} 16 , $$
cf. the overview [3].
C) For a regular complete intersection, if $ n $ is even, $ A $ is an $ ( M- 1) $- variety and the inclusion homomorphism
$$ i _ {*} : H _ {n / 2 } ( A ; \mathbf Z _ {2} ) \rightarrow H _ {n / 2 } ( \mathbf R P ^ {q} ; \mathbf Z _ {2} ) $$
is zero, then
$$ d = m _ {1} m _ {2} \dots \equiv 2 \mathop{\rm mod} 4 $$
and
$$ \chi ( A ) \equiv - \sigma ( \mathbf C A ) + \left \{ \begin{array}{rl} 2 \mathop{\rm mod} 16 & \textrm{ if } d \equiv 2 \mathop{\rm mod} 8 , \\ - 2 \mathop{\rm mod} 16 & \textrm{ if } d \equiv - 2 \mathop{\rm mod} 8 . \\ \end{array} \right .$$
In this case, if $ n $ is even, $ A $ is an $ ( M- 2) $- variety and $ i _ {*} $ is zero ([11]):
if $ d \equiv 0 $ $ \mathop{\rm mod} 8 $, $ \chi ( A) \equiv \pm \sigma ( \mathbf C A ) $ $ \mathop{\rm mod} 16 $,
if $ d \equiv 2 $ $ \mathop{\rm mod} 8 $, $ \chi ( A) \equiv - \sigma ( \mathbf C A ) + 4 $ $ \mathop{\rm mod} 16 $ or $ \chi ( A) \equiv \pm \sigma ( \mathbf C A ) $ $ \mathop{\rm mod} 16 $,
if $ d \begin{array}{c} > \\ = \end{array} 2 $ $ \mathop{\rm mod} 8 $, $ \chi ( A) \equiv - \sigma ( \mathbf C A ) - 4 $ $ \mathop{\rm mod} 16 $ or $ \chi ( A) \equiv \pm \sigma ( \mathbf C A ) $ $ \mathop{\rm mod} 16 $.
In particular, for a real algebraic surface $ A $ of order $ m _ {1} $,
$$ \mathop{\rm dim} H _ {*} ( \mathbf C A ; \mathbf Z _ {2} ) = m _ {1} ^ {3} - 4 m _ {1} ^ {2} + 6 m _ {1} . $$
If $ A $ is an $ M $- surface, then
$$ \chi ( A) \equiv \frac{1}{3} ( 4 m _ {1} - m _ {1} ^ {3} ) \mathop{\rm mod} 16 . $$
If $ A $ is an $ ( M- 1) $- surface, then
$$ \chi ( A) \equiv \frac{1}{3} ( 4 m _ {1} - m _ {1} ^ {3} ) \pm 2 \mathop{\rm mod} 16 . $$
If $ A $ is an $ ( M- 1) $- surface and contracts to a point in $ \mathbf R P ^ {3} $, then $ m _ {1} \equiv 2 $ $ \mathop{\rm mod} 4 $ and
$$ \chi ( A) \equiv \left \{ \begin{array}{rl} 2 \mathop{\rm mod} 16 & \textrm{ if } m _ {1} \equiv 2 \mathop{\rm mod} 8 , \\ - 2 \mathop{\rm mod} 16 & \textrm{ if } m _ {1} \equiv - 2 \mathop{\rm mod} 8 . \\ \end{array} \right . $$
If $ A $ is an $ ( M- 2) $- surface and contracts to a point in $ \mathbf R P ^ {3} $, then
$$ \chi ( A) \equiv \left \{ \begin{array}{rl} 0 \mathop{\rm mod} 16 & \textrm{ if } m _ {1} \equiv 0 \mathop{\rm mod} 8, \\ 0 , 4 \mathop{\rm mod} 16 & \textrm{ if } m _ {1} \equiv 2 \mathop{\rm mod} 8 , \\ 0 , - 4 \mathop{\rm mod} 16 & \textrm{ if } m _ {1} \equiv - 2 \mathop{\rm mod} 8 . \\ \end{array} \right .$$
Certain congruences have also been proved , [13] for odd $ n $. In particular, for a plane real algebraic curve $ A $ which is an $ ( M- 1) $- curve of even order $ m _ {1} $:
$$ P - N \equiv \left ( \frac{m _ 1}{2} \right ) ^ {2} \pm 1 \mathop{\rm mod} 8 . $$
Certain results have also been obtained [13] for real algebraic varieties with singularities. For an interesting approach to the study of real algebraic varieties see [14].
References
| [1] | A. Harnack, "Ueber die Vieltheitigkeit der ebenen algebraischen Kurven" Math. Ann. , 10 (1876) pp. 189–198 |
| [2] | D. Hilbert, "Ueber die reellen Züge algebraischer Kurven" Math. Ann. , 38 (1891) pp. 115–138 |
| [3] | D. Hilbert, "Mathematische Probleme" Arch. Math. Phys. , 1 (1901) pp. 213–237 Zbl 32.0084.05 |
| [4] | I.G. Petrovskii, "On the topology of real plane algebraic curves" Ann. of Math. , 39 : 1 (1938) pp. 189–209 MR1503398 |
| [5] | O.A. Oleinik, I.G. Petrovskii, "On the topology of real algebraic surfaces" Transl. Amer. Math. Soc. , 7 (1952) pp. 399–417 Izv. Akad. Nauk SSSR Ser. Mat. , 13 (1949) pp. 389–402 MR0048095 |
| [6] | O.A. Oleinik, "On the topology of real algebraic curves on an algebraic surface" Mat. Sb. , 29 (1951) pp. 133–156 (In Russian) MR44863 |
| [7] | , Hilbert problems , Moscow (1969) (In Russian) Zbl 0187.35502 Zbl 0186.18601 Zbl 0181.15503 |
| [8] | V.I. Arnol'd, "Distribution of the ovals of the real plane of algebraic curves, of involutions of four-dimensional smooth manifolds, and the arithmetic of integer-valued quadratic forms" Funct. Anal. Appl. , 5 : 3 (1971) pp. 169–176 Funkts. Anal. , 5 : 3 (1971) pp. 1–9 Zbl 0268.53001 |
| [9a] | V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" Funct. Anal. Appl. , 6 : 4 (1972) pp. 301–306 Funkts. Anal. , 6 : 4 (1972) pp. 58–64 |
| [9b] | V.A. Rokhlin, "Congruences modulo 16 in Hilbert's sixteenth problem" Funct. Anal. Appl. , 7 : 2 (1973) pp. 163–165 Funkts. Anal. , 7 : 2 (1973) pp. 91–92 |
| [10a] | V.M. Kharlamov, "A generalized Petrovskii inequality" Funct. Anal. Appl. , 8 : 2 (1974) pp. 132–137 Funkts. Anal. , 8 : 2 (1974) pp. 50–56 Zbl 0301.14021 |
| [10b] | V.M. Kharlamov, "A generalized Petrovskii inequality II" Funct. Anal. Appl. , 9 : 3 (1975) pp. 266–268 Funkts. Anal. , 9 : 3 (1975) pp. 93–94 |
| [11] | V.M. Kharlamov, "Additive congruences for the Euler characteristic of real algebraic manifolds of even dimensions" Funct. Anal. Appl. , 9 : 2 (1975) pp. 134–141 Funkts. Anal. , 9 : 2 (1975) pp. 51–60 |
| [12] | V.M. Kharlamov, "The topological type of nonsingular surfaces in 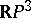 of degree four" Funct. Anal. Appl. , 10 : 4 (1976) pp. 295–304 Funkts. Anal. , 10 : 4 (1976) pp. 55–68 Zbl 0362.14013 of degree four" Funct. Anal. Appl. , 10 : 4 (1976) pp. 295–304 Funkts. Anal. , 10 : 4 (1976) pp. 55–68 Zbl 0362.14013 |
| [13] | D.A. Gudkov, "The topology of real projective algebraic varieties" Russian Math. Surveys , 29 : 4 (1974) pp. 1–80 Uspekhi Mat. Nauk , 29 : 4 (1974) pp. 3–79 MR0399085 Zbl 0316.14018 |
| [14] | D. Sullivan, "Geometric topology" , I. Localization, periodicity, and Galois symmetry , M.I.T. (1971) MR0494074 MR0494075 Zbl 1078.55001 Zbl 0871.57021 Zbl 0366.57003 |
Comments
References
| [a1] | O. Viro, "Successes of the last five years in the topology of real algebraic varieties" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & North-Holland (1984) pp. 603–619 |
| [a2] | G. Wilson, "Hilbert's sixteenth problem" Topology , 17 (1978) pp. 53–74 |
Real algebraic variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Real_algebraic_variety&oldid=55105