Difference between revisions of "Banaschewski compactification"
From Encyclopedia of Mathematics
m (link) |
(latex details) |
||
| Line 1: | Line 1: | ||
| − | A [[ | + | A [[topological space]] $X$ is $0$-dimensional if it is a $T_1$-space (cf. also [[Separation axiom|Separation axiom]]) with a base of [[clopen]] sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [[#References|[a1]]], [[#References|[a2]]] of $X$, denoted by $\beta_0 X$, is the $0$-dimensional analogue of the [[Stone–Čech compactification]] of a [[Tikhonov space]]. It can be obtained as the [[Stone space]] of the [[Boolean algebra]] of clopen subsets. |
| − | The Banaschewski compactification is also a special case of the [[ | + | The Banaschewski compactification is also a special case of the [[Wallman compactification]] [[#References|[a4]]] (as generalized by N.A. Shanin, [[#References|[a3]]]). A fairly general approach subsuming the above-mentioned compactifications is as follows. |
| − | Let | + | Let $X$ be an arbitrary non-empty set and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101209.png" /> a [[Lattice|lattice]] of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012010.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012011.png" />. Assume that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012012.png" /> is disjunctive and separating, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012013.png" /> be the [[Algebra|algebra]] generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012014.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012015.png" /> be the set of non-trivial zero-one valued finitely additive measures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012016.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012017.png" /> be the set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012018.png" /> that are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012019.png" />-regular, i.e., |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012020.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b11012020.png" /></td> </tr></table> | ||
| Line 21: | Line 21: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Banaschewski, "Über nulldimensional Räume" ''Math. Nachr.'' , '''13''' (1955) pp. 129–140</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Banaschewski, "On Wallman's method of compactification" ''Math. Nachr.'' , '''27''' (1963) pp. 105–114</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.A. Shanin, "On the theory of bicompact extensions of topological spaces" ''Dokl. Aka. Nauk SSSR'' , '''38''' (1943) pp. 154–156 (In Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Wallman, "Lattices and topological spaces" ''Ann. Math.'' , '''39''' (1938) pp. 112–126</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Banaschewski, "Über nulldimensional Räume" ''Math. Nachr.'' , '''13''' (1955) pp. 129–140</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> B. Banaschewski, "On Wallman's method of compactification" ''Math. Nachr.'' , '''27''' (1963) pp. 105–114</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.A. Shanin, "On the theory of bicompact extensions of topological spaces" ''Dokl. Aka. Nauk SSSR'' , '''38''' (1943) pp. 154–156 (In Russian)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Wallman, "Lattices and topological spaces" ''Ann. Math.'' , '''39''' (1938) pp. 112–126</TD></TR></table> | ||
| + | |||
| + | {{TEX|want}} | ||
Revision as of 20:23, 14 December 2023
A topological space $X$ is $0$-dimensional if it is a $T_1$-space (cf. also Separation axiom) with a base of clopen sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [a1], [a2] of $X$, denoted by $\beta_0 X$, is the $0$-dimensional analogue of the Stone–Čech compactification of a Tikhonov space. It can be obtained as the Stone space of the Boolean algebra of clopen subsets.
The Banaschewski compactification is also a special case of the Wallman compactification [a4] (as generalized by N.A. Shanin, [a3]). A fairly general approach subsuming the above-mentioned compactifications is as follows.
Let $X$ be an arbitrary non-empty set and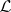 
a lattice of subsets of 
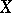such that 
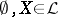. Assume that 
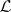is disjunctive and separating, let 
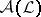be the algebra generated by 
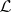, let 
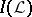be the set of non-trivial zero-one valued finitely additive measures on 
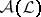, and let 
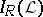be the set of elements 
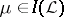that are 
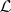-regular, i.e.,
 |
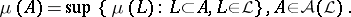One can identify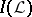 
with the 
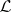-prime filters and 
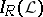with the 
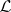-ultrafilters (cf. also Filter; Ultrafilter).
Next, let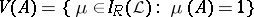 
, where 
; 
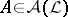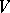is a lattice isomorphism from 
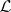to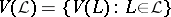 
. Take 
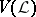as a base for the closed sets of a topology 
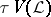on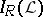 
. Then 
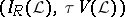is a compact 
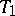-space and it is 
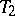(cf. Hausdorff space) if and only if 
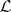is a normal lattice. 
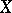can be densely imbedded in 
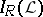by the mapping 
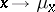, where 
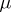is the Dirac measure concentrated at 
(cf. also Dirac delta-function). The mapping is a homeomorphism if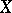 
is given the topology of closed sets with 
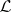as base for the closed sets.
If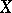 
is a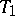 
-space and 
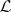is the lattice of closed sets, then 
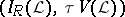becomes the usual Wallman compactification 
.
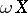If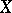 
is a Tikhonov space and 
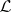is the lattice of zero sets, then 
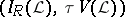becomes the Stone–Čech compactification 
.
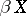If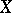 
is a 
-dimensional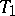 
-space and 
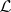is the lattice of clopen sets, then 
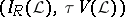becomes the Banaschewski compactification 
.
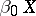if and only if 
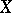is a normal space; 
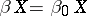if and only if 
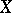is strongly 
-dimensional (i.e., the clopen sets separate the zero sets).
References
| [a1] | B. Banaschewski, "Über nulldimensional Räume" Math. Nachr. , 13 (1955) pp. 129–140 |
| [a2] | B. Banaschewski, "On Wallman's method of compactification" Math. Nachr. , 27 (1963) pp. 105–114 |
| [a3] | N.A. Shanin, "On the theory of bicompact extensions of topological spaces" Dokl. Aka. Nauk SSSR , 38 (1943) pp. 154–156 (In Russian) |
| [a4] | H. Wallman, "Lattices and topological spaces" Ann. Math. , 39 (1938) pp. 112–126 |
How to Cite This Entry:
Banaschewski compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banaschewski_compactification&oldid=54784
Banaschewski compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banaschewski_compactification&oldid=54784
This article was adapted from an original article by G. Bachman (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article