Difference between revisions of "Tits quadratic form"
m (Automatically changed introduction) |
m (gt to >) |
||
| Line 29: | Line 29: | ||
where $r_{i, j} = | L \cap e _ { j } I e _ { i } |$, for a minimal set $L$ of generators of $I$ contained in $\sum _ { i , j \in Q _ { 0 } } e _ { j } I { e }_i$. One checks that $r_{i,\,j} = \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { 2 } ( S _ { j } , S _ { i } )$, where $S _ { t }$ is the simple $R$-module associated to the vertex $t \in Q_0$. Then the definition of $q_{ R}$ depends only on $R$, and when $R$ is of global dimension at most two, the form $q_{ R}$ coincides with the Euler characteristic $\chi _ { R } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf Z$, $[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$, under a group isomorphism $\underline{\operatorname { dim }} : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf{Z} ^ { Q _ { 0 } }$, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140120.png"/> is the [[Grothendieck group|Grothendieck group]] of the category $\operatorname{mod} R$ of finite-dimensional right $R$-modules (see [[#References|[a17]]]). Note that $q_R = q_Q$ if $R = K Q$. | where $r_{i, j} = | L \cap e _ { j } I e _ { i } |$, for a minimal set $L$ of generators of $I$ contained in $\sum _ { i , j \in Q _ { 0 } } e _ { j } I { e }_i$. One checks that $r_{i,\,j} = \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { 2 } ( S _ { j } , S _ { i } )$, where $S _ { t }$ is the simple $R$-module associated to the vertex $t \in Q_0$. Then the definition of $q_{ R}$ depends only on $R$, and when $R$ is of global dimension at most two, the form $q_{ R}$ coincides with the Euler characteristic $\chi _ { R } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf Z$, $[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$, under a group isomorphism $\underline{\operatorname { dim }} : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf{Z} ^ { Q _ { 0 } }$, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140120.png"/> is the [[Grothendieck group|Grothendieck group]] of the category $\operatorname{mod} R$ of finite-dimensional right $R$-modules (see [[#References|[a17]]]). Note that $q_R = q_Q$ if $R = K Q$. | ||
| − | By applying a Tits-type equality as above, Bongartz [[#References|[a3]]] proved that if $R$ is of finite representation type, then $q_{ R}$ is weakly positive, that is, $q _ { R } ( v ) | + | By applying a Tits-type equality as above, Bongartz [[#References|[a3]]] proved that if $R$ is of finite representation type, then $q_{ R}$ is weakly positive, that is, $q _ { R } ( v ) > 0$ for all non-zero vectors $v \in {\bf N} ^ { n }$. The converse implication does not hold in general, but it has been established if the Auslander–Reiten quiver of $R$ (see [[Riedtmann classification]]) has a post-projective component (see [[#References|[a10]]]), by applying an idea of Drozd [[#References|[a5]]]. J.A. de la Peña [[#References|[a14]]] proved that if $R$ is of tame representation type, then $q_{ R}$ is weakly non-negative. The converse implication does not hold in general, but it has been proved under a suitable assumption on $R$ (see [[#References|[a13]]] and [[#References|[a16]]] for a discussion of this problem and relations between the Tits quadratic form and the Euler quadratic form of $R$). |
Let $( I , \preceq )$ be a partially ordered set with partial order relation $\preceq$ and let $\operatorname { max}I$ be the set of all maximal elements of $( I , \preceq )$. Following [[#References|[a5]]] and [[#References|[a15]]], D. Simson [[#References|[a20]]] defined the Tits quadratic form $q_l : \mathbf{Z} ^ { l } \rightarrow \mathbf{Z}$ of $( I , \preceq )$ by the formula | Let $( I , \preceq )$ be a partially ordered set with partial order relation $\preceq$ and let $\operatorname { max}I$ be the set of all maximal elements of $( I , \preceq )$. Following [[#References|[a5]]] and [[#References|[a15]]], D. Simson [[#References|[a20]]] defined the Tits quadratic form $q_l : \mathbf{Z} ^ { l } \rightarrow \mathbf{Z}$ of $( I , \preceq )$ by the formula | ||
| Line 42: | Line 42: | ||
====References==== | ====References==== | ||
| − | <table><tr><td valign="top">[a1]</td> <td valign="top"> V.I. Auslander, I. Reiten, S. Smalø, "Representation theory of Artin algebras" , ''Studies Adv. Math.'' , '''36''' , Cambridge Univ. Press (1995) {{MR|1314422}} {{ZBL|0834.16001}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> I.N. Bernstein, I.M. Gelfand, V.A. Ponomarev, "Coxeter functors and Gabriel's theorem" ''Russian Math. Surveys'' , '''28''' (1973) pp. 17–32 ''Uspekhi Mat. Nauk.'' , '''28''' (1973) pp. 19–33 {{MR|393065}} {{ZBL|}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K. Bongartz, "Algebras and quadratic forms" ''J. London Math. Soc.'' , '''28''' (1983) pp. 461–469 {{MR|0724715}} {{ZBL|0532.16020}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Dlab, C.M. Ringel, "Indecomposable representations of graphs and algebras" , ''Memoirs'' , '''173''' , Amer. Math. Soc. (1976) {{MR|0447344}} {{ZBL|0332.16015}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> Yu.A. Drozd, "Coxeter transformations and representations of partially ordered sets" ''Funkts. Anal. Prilozhen.'' , '''8''' (1974) pp. 34–42 (In Russian) {{MR|0351924}} {{ZBL|0356.06003}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> Yu.A. Drozd, "On tame and wild matrix problems" , ''Matrix Problems'' , Akad. Nauk. Ukr. SSR., Inst. Mat. Kiev (1977) pp. 104–114 (In Russian) {{MR|498704}} {{ZBL|}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> Yu.A. Drozd, "Tame and wild matrix problems" , ''Representations and Quadratic Forms'' (1979) pp. 39–74 (In Russian) {{MR|0600111}} {{ZBL|0454.16014}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> P. Gabriel, "Unzerlegbare Darstellungen 1" ''Manuscripta Math.'' , '''6''' (1972) pp. 71–103 (Also: Berichtigungen 6 (1972), 309) {{MR|332887}} {{ZBL|}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> P. Gabriel, "Représentations indécomposables" , ''Séminaire Bourbaki (1973/74)'' , ''Lecture Notes in Mathematics'' , '''431''' , Springer (1975) pp. 143–169 {{MR|0485996}} {{ZBL|0335.17005}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> P. Gabriel, A.V. Roiter, "Representations of finite dimensional algebras" , ''Algebra VIII'' , ''Encycl. Math. Stud.'' , '''73''' , Springer (1992) {{MR|1239446}} {{MR|1239447}} {{ZBL|0839.16001}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Kasjan, D. Simson, "Tame prinjective type and Tits form of two-peak posets II" ''J. Algebra'' , '''187''' (1997) pp. 71–96 {{MR|1425560}} {{ZBL|0944.16013}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> L.A. Nazarova, "Representations of quivers of infinite type" ''Izv. Akad. Nauk. SSSR'' , '''37''' (1973) pp. 752–791 (In Russian) {{MR|0338018}} {{ZBL|0298.15012}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> J.A. de la Peña, "Algebras with hypercritical Tits form" , ''Topics in Algebra'' , ''Banach Center Publ.'' , '''26: 1''' , PWN (1990) pp. 353–369 {{MR|}} {{ZBL|0731.16008}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> J.A. de la Peña, "On the dimension of the module-varieties of tame and wild algebras" ''Commun. Algebra'' , '''19''' (1991) pp. 1795–1807 {{MR|}} {{ZBL|0818.16013}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> J.A. de la Peña, D. Simson, "Prinjective modules, reflection functors, quadratic forms and Auslander–Reiten sequences" ''Trans. Amer. Math. Soc.'' , '''329''' (1992) pp. 733–753 {{MR|1025753}} {{ZBL|0789.16010}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> J.A. de la Peña, A. Skowroński, "The Euler and Tits forms of a tame algebra" ''Math. Ann.'' , '''315''' (2000) pp. 37–59 {{MR|}} {{ZBL|0941.16010}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> C.M. Ringel, "Tame algebras and integral quadratic forms" , ''Lecture Notes in Mathematics'' , '''1099''' , Springer (1984) {{MR|0774589}} {{ZBL|0546.16013}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> A.V. Roiter, M.M. Kleiner, "Representations of differential graded categories" , ''Lecture Notes in Mathematics'' , '''488''' , Springer (1975) pp. 316–339 {{MR|0435145}} {{ZBL|0356.16011}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> D. Simson, "Linear representations of partially ordered sets and vector space categories" , ''Algebra, Logic Appl.'' , '''4''' , Gordon & Breach (1992) {{MR|1241646}} {{ZBL|0818.16009}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> D. Simson, "Posets of finite prinjective type and a class of orders" ''J. Pure Appl. Algebra'' , '''90''' (1993) pp. 77–103 {{MR|1246276}} {{ZBL|0815.16006}} </td></tr><tr><td valign="top">[a21]</td> <td valign="top"> D. Simson, "Representation types, Tits reduced quadratic forms and orbit problems for lattices over orders" ''Contemp. Math.'' , '''229''' (1998) pp. 307–342 {{MR|1676228}} {{ZBL|0921.16007}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> D. Simson, "Coalgebras, comodules, pseudocompact algebras and tame comodule type" ''Colloq. Math.'' , '''in press''' (2001) {{MR|1874368}} {{ZBL|1055.16038}} </td></tr></table> | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> V.I. Auslander, I. Reiten, S. Smalø, "Representation theory of Artin algebras" , ''Studies Adv. Math.'' , '''36''' , Cambridge Univ. Press (1995) {{MR|1314422}} {{ZBL|0834.16001}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> I.N. Bernstein, I.M. Gelfand, V.A. Ponomarev, "Coxeter functors and Gabriel's theorem" ''Russian Math. Surveys'' , '''28''' (1973) pp. 17–32 ''Uspekhi Mat. Nauk.'' , '''28''' (1973) pp. 19–33 {{MR|393065}} {{ZBL|}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> K. Bongartz, "Algebras and quadratic forms" ''J. London Math. Soc.'' , '''28''' (1983) pp. 461–469 {{MR|0724715}} {{ZBL|0532.16020}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Dlab, C.M. Ringel, "Indecomposable representations of graphs and algebras" , ''Memoirs'' , '''173''' , Amer. Math. Soc. (1976) {{MR|0447344}} {{ZBL|0332.16015}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> Yu.A. Drozd, "Coxeter transformations and representations of partially ordered sets" ''Funkts. Anal. Prilozhen.'' , '''8''' (1974) pp. 34–42 (In Russian) {{MR|0351924}} {{ZBL|0356.06003}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> Yu.A. Drozd, "On tame and wild matrix problems" , ''Matrix Problems'' , Akad. Nauk. Ukr. SSR., Inst. Mat. Kiev (1977) pp. 104–114 (In Russian) {{MR|498704}} {{ZBL|}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> Yu.A. Drozd, "Tame and wild matrix problems" , ''Representations and Quadratic Forms'' (1979) pp. 39–74 (In Russian) {{MR|0600111}} {{ZBL|0454.16014}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> P. Gabriel, "Unzerlegbare Darstellungen 1" ''Manuscripta Math.'' , '''6''' (1972) pp. 71–103 (Also: Berichtigungen 6 (1972), 309) {{MR|332887}} {{ZBL|}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> P. Gabriel, "Représentations indécomposables" , ''Séminaire Bourbaki (1973/74)'' , ''Lecture Notes in Mathematics'' , '''431''' , Springer (1975) pp. 143–169 {{MR|0485996}} {{ZBL|0335.17005}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> P. Gabriel, A.V. Roiter, "Representations of finite dimensional algebras" , ''Algebra VIII'' , ''Encycl. Math. Stud.'' , '''73''' , Springer (1992) {{MR|1239446}} {{MR|1239447}} {{ZBL|0839.16001}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S. Kasjan, D. Simson, "Tame prinjective type and Tits form of two-peak posets II" ''J. Algebra'' , '''187''' (1997) pp. 71–96 {{MR|1425560}} {{ZBL|0944.16013}} </td></tr><tr><td valign="top">[a12]</td> <td valign="top"> L.A. Nazarova, "Representations of quivers of infinite type" ''Izv. Akad. Nauk. SSSR'' , '''37''' (1973) pp. 752–791 (In Russian) {{MR|0338018}} {{ZBL|0298.15012}} </td></tr><tr><td valign="top">[a13]</td> <td valign="top"> J.A. de la Peña, "Algebras with hypercritical Tits form" , ''Topics in Algebra'' , ''Banach Center Publ.'' , '''26: 1''' , PWN (1990) pp. 353–369 {{MR|}} {{ZBL|0731.16008}} </td></tr><tr><td valign="top">[a14]</td> <td valign="top"> J.A. de la Peña, "On the dimension of the module-varieties of tame and wild algebras" ''Commun. Algebra'' , '''19''' (1991) pp. 1795–1807 {{MR|}} {{ZBL|0818.16013}} </td></tr><tr><td valign="top">[a15]</td> <td valign="top"> J.A. de la Peña, D. Simson, "Prinjective modules, reflection functors, quadratic forms and Auslander–Reiten sequences" ''Trans. Amer. Math. Soc.'' , '''329''' (1992) pp. 733–753 {{MR|1025753}} {{ZBL|0789.16010}} </td></tr><tr><td valign="top">[a16]</td> <td valign="top"> J.A. de la Peña, A. Skowroński, "The Euler and Tits forms of a tame algebra" ''Math. Ann.'' , '''315''' (2000) pp. 37–59 {{MR|}} {{ZBL|0941.16010}} </td></tr><tr><td valign="top">[a17]</td> <td valign="top"> C.M. Ringel, "Tame algebras and integral quadratic forms" , ''Lecture Notes in Mathematics'' , '''1099''' , Springer (1984) {{MR|0774589}} {{ZBL|0546.16013}} </td></tr><tr><td valign="top">[a18]</td> <td valign="top"> A.V. Roiter, M.M. Kleiner, "Representations of differential graded categories" , ''Lecture Notes in Mathematics'' , '''488''' , Springer (1975) pp. 316–339 {{MR|0435145}} {{ZBL|0356.16011}} </td></tr><tr><td valign="top">[a19]</td> <td valign="top"> D. Simson, "Linear representations of partially ordered sets and vector space categories" , ''Algebra, Logic Appl.'' , '''4''' , Gordon & Breach (1992) {{MR|1241646}} {{ZBL|0818.16009}} </td></tr><tr><td valign="top">[a20]</td> <td valign="top"> D. Simson, "Posets of finite prinjective type and a class of orders" ''J. Pure Appl. Algebra'' , '''90''' (1993) pp. 77–103 {{MR|1246276}} {{ZBL|0815.16006}} </td></tr><tr><td valign="top">[a21]</td> <td valign="top"> D. Simson, "Representation types, Tits reduced quadratic forms and orbit problems for lattices over orders" ''Contemp. Math.'' , '''229''' (1998) pp. 307–342 {{MR|1676228}} {{ZBL|0921.16007}} </td></tr><tr><td valign="top">[a22]</td> <td valign="top"> D. Simson, "Coalgebras, comodules, pseudocompact algebras and tame comodule type" ''Colloq. Math.'' , '''in press''' (2001) {{MR|1874368}} {{ZBL|1055.16038}} </td></tr> | ||
| + | </table> | ||
Revision as of 10:24, 11 November 2023
Let $Q = ( Q _ { 0 } , Q _ { 1 } )$ be a finite quiver (see [a8]), that is, an oriented graph with vertex set $Q_0$ and set $Q _ { 1 }$ of arrows (oriented edges; cf. also Graph, oriented; Quiver). Following P. Gabriel [a8], [a9], the Tits quadratic form $q_{Q} : \mathbf{Z} ^ { Q _ { 0 } } \rightarrow \mathbf{Z} $ of $Q$ is defined by the formula
\begin{equation*} q_Q ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { i , j \in Q _ { 0 } } d _ { i j } x _ { i } x _ { j }, \end{equation*}
where $x = ( x _ { i } ) _ { i \in Q _ { 0 } } \in \mathbf{Z} ^ { Q _ { 0 } }$ and $d _ { i j}$ is the number of arrows from $i$ to $j$ in $Q _ { 1 }$.
There are important applications of the Tits form in representation theory. One easily proves that if $Q$ is connected, then $q_Q$ is positive definite if and only if $Q$ (viewed as a non-oriented graph) is any of the Dynkin diagrams $\mathbf{A} _ { n }$, ${\bf D} _ { n }$, ${\bf E} _ { 6 }$, $\mathbf{E} _ { 7 }$, or $\mathbf{E} _ { 8 }$ (cf. also Dynkin diagram). On the other hand, the Gabriel theorem [a8] asserts that this is the case if and only if $Q$ has only finitely many isomorphism classes of indecomposable $K$-linear representations, where $K$ is an algebraically closed field (see also [a2]). Let $\operatorname{rep}_K( Q )$ be the Abelian category of finite-dimensional $K$-linear representations of $Q$ formed by the systems $\mathbf{X} = ( X _ { i } , \phi _ { \beta } ) _ { j \in Q _ { 0 } , \beta \in Q _ { 1 }}$ of finite-dimensional vector $K$-spaces $X_j$, connected by $K$-linear mappings $\phi _ { \beta } : X _ { i } \rightarrow X _ { j }$ corresponding to arrows $\beta : i \rightarrow j$ of $Q$. By a theorem of L.A. Nazarova [a12], given a connected quiver $Q$ the category $\operatorname{rep}_K( Q )$ is of tame representation type (see [a7], [a10], [a19] and Quiver) if and only if $q_Q$ is positive semi-definite, or equivalently, if and only if $Q$ (viewed as a non-oriented graph) is any of the extended Dynkin diagrams $\tilde { A }_{ n }$, $\tilde { \mathbf{D} } _ { n }$, $\widetilde{\bf E} _ { 6 }$, $\tilde{\mathbf{E}} _ { 7 }$, or $\tilde{\bf E} _ { 8 }$ (see [a1], [a10], [a19]; and [a4] for a generalization).
Let $K _ { 0 } ( Q ) = K _ { 0 } ( \operatorname { rep } _ { K } ( Q ) )$ be the Grothendieck group of the category $\operatorname{rep}_K( Q )$. By the Jordan–Hölder theorem, the correspondence $\mathbf{X} \mapsto \underline{\operatorname { dim }} \mathbf{X} = ( \operatorname { dim } _ { K } X _ { j } ) _ { j \in Q _ { 0 } }$ defines a group isomorphism $\underline{\operatorname { dim }} : K _ { 0 } ( Q ) \rightarrow \mathbf{Z} ^ { Q _ { 0 } }$. One shows that the Tits form $q_Q$ coincides with the Euler characteristic $\chi _ { Q } : K _ { 0 } ( Q ) \rightarrow \mathbf{Z}$, $[ \mathbf{X} ] \mapsto \chi _ { Q } ( [ \mathbf{X} ] ) = \operatorname { dim } _ { K } \operatorname { End } _ { Q } ( \mathbf{X} ) - \operatorname { dim } _ { K } \operatorname { Ext } _ { Q } ^ { 1 } ( \mathbf{X} , \mathbf{X} )$, along the isomorphism $\underline{\operatorname { dim }} : K _ { 0 } ( Q ) \rightarrow \mathbf{Z} ^ { Q _ { 0 } }$, that is, $q_{Q} ( \underline { \operatorname { dim } } \mathbf{X} ) = \chi _ { Q } ( [ \mathbf{X} ] )$ for any $\mathbf{X}$ in $\operatorname{rep}_K( Q )$ (see [a10], [a17]).
The Tits quadratic form $q_Q$ is related with an algebraic geometry context defined as follows (see [a9], [a10], [a19]).
For any vector $v = ( v _ { j } ) _ { j \in Q _ { 0 } } \in \mathbf{N} ^ { Q _ { 0 } }$, consider the affine irreducible $K$-variety $\mathcal{A} _ { Q } ( v ) = \prod _ { i ,\, j \in Q _ { 0 } } \prod _ { ( \beta : j \rightarrow i ) \in Q _ { 1 } } \mathbf{M} _ { v _ { i } \times v _ { j } } ( K ) _ { \beta }$ of $K$-representations of $Q$ of the dimension type $v$ (in the Zariski topology), where $\mathbf{M} _ { v _ { i } \times v _ { j } } ( K ) _ { \beta } = \mathbf{M} _ { v _ { i } \times v _ { j } } ( K )$ is the space of $( v _ { i } \times v _ { j } )$-matrices for any arrow $\beta : j \rightarrow i$ of $Q$. Consider the algebraic group ${\cal G} \operatorname{l} _ { Q } ( d ) = \prod _ { j \in Q _ { 0 } } \operatorname{Gl} ( v _ { j } , K )$ and the algebraic group action $* : \mathcal{G} \text{l} _ { Q } ( d ) \times \mathcal{A} _ { Q } ( d ) \rightarrow \mathcal{A} _ { Q } ( d )$ defined by the formula $( h _ { j } ) ^ { * } ( M _ { i j } ^ { \beta } ) = ( h _ { i } ^ { - 1 } M _ { i j } ^ { \beta } h _ { j } )$, where $\beta : j \rightarrow i$ is an arrow of $Q$, $M _ { i j } ^ { \beta } \in \mathbf{M} _ { v _ { j } \times v _ { i } } ( K ) _ { \beta }$, $h _ { j } \in \operatorname{Gl} ( v _ { j } , K )$, and $h _ { i } \in \operatorname{Gl} ( v _ { i } , K )$. An important role in applications is played by the Tits-type equality $q_Q ( v ) = \operatorname { dim } {\cal G}\operatorname{l} _ { Q } ( v ) - \operatorname { dim } {\cal A} _ { Q } ( v )$, $v \in \mathbf N ^ { Q _ 0}$, where  denotes the dimension of the algebraic variety (see [a8]).
denotes the dimension of the algebraic variety (see [a8]).
Following the above ideas, Yu.A. Drozd [a5] introduced and successfully applied a Tits quadratic form in the study of finite representation type of the Krull–Schmidt category 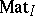 of matrix $K$-representations of partially ordered sets $( I , \preceq )$ with a unique maximal element (see [a10], [a19]). In [a6] and [a7] he also studied bimodule matrix problems and the representation type of boxes $\mathcal{B}$ by means of an associated Tits quadratic form $q_{\cal B} : {\bf Z} ^ { n } \rightarrow {\bf Z}$ (see also [a18]). In particular, he showed [a6] that if $\mathcal{B}$ is of tame representation type, then $q_{\mathcal{B}}$ is weakly non-negative, that is, $q _ { \mathcal B } ( v ) \geq 0$ for all $v \in {\bf N} ^ { n }$.
of matrix $K$-representations of partially ordered sets $( I , \preceq )$ with a unique maximal element (see [a10], [a19]). In [a6] and [a7] he also studied bimodule matrix problems and the representation type of boxes $\mathcal{B}$ by means of an associated Tits quadratic form $q_{\cal B} : {\bf Z} ^ { n } \rightarrow {\bf Z}$ (see also [a18]). In particular, he showed [a6] that if $\mathcal{B}$ is of tame representation type, then $q_{\mathcal{B}}$ is weakly non-negative, that is, $q _ { \mathcal B } ( v ) \geq 0$ for all $v \in {\bf N} ^ { n }$.
K. Bongartz [a3] associated with any finite-dimensional basic $K$-algebra $R$ a Tits quadratic form as follows. Let $\{ e _ { 1 } , \ldots , e _ { n } \}$ be a complete set of primitive pairwise non-isomorphic orthogonal idempotents of the algebra $R$. Fix a finite quiver $Q = ( Q _ { 0 } , Q _ { 1 } )$ with $Q _ { 0 } = \{ 1 , \ldots , n \}$ and a $K$-algebra isomorphism $R \simeq K Q / I$, where $K Q$ is the path $K$-algebra of the quiver $Q$ (see [a1], [a10], [a19]) and $I$ is an ideal of $R$ contained in the square of the Jacobson radical $\operatorname{rad} R$ of $R$ and containing a power of $\operatorname{rad} R$. Assume that $Q$ has no oriented cycles (and hence the global dimension of $R$ is finite). The Tits quadratic form $q_R : {\bf Z} ^ { n } \rightarrow \bf Z$ of $R$ is defined by the formula
\begin{equation*} q_{ R} ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ {( \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { i } x _ { j } + \sum _ { ( \beta : i \rightarrow j ) \in Q _ { 1 } } r _ { i ,\, j } x _ { i } x _ { j }, \end{equation*}
where $r_{i, j} = | L \cap e _ { j } I e _ { i } |$, for a minimal set $L$ of generators of $I$ contained in $\sum _ { i , j \in Q _ { 0 } } e _ { j } I { e }_i$. One checks that $r_{i,\,j} = \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { 2 } ( S _ { j } , S _ { i } )$, where $S _ { t }$ is the simple $R$-module associated to the vertex $t \in Q_0$. Then the definition of $q_{ R}$ depends only on $R$, and when $R$ is of global dimension at most two, the form $q_{ R}$ coincides with the Euler characteristic $\chi _ { R } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf Z$, $[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$, under a group isomorphism $\underline{\operatorname { dim }} : K _ { 0 } ( \operatorname { mod } R ) \rightarrow \mathbf{Z} ^ { Q _ { 0 } }$, where 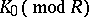 is the Grothendieck group of the category $\operatorname{mod} R$ of finite-dimensional right $R$-modules (see [a17]). Note that $q_R = q_Q$ if $R = K Q$.
is the Grothendieck group of the category $\operatorname{mod} R$ of finite-dimensional right $R$-modules (see [a17]). Note that $q_R = q_Q$ if $R = K Q$.
By applying a Tits-type equality as above, Bongartz [a3] proved that if $R$ is of finite representation type, then $q_{ R}$ is weakly positive, that is, $q _ { R } ( v ) > 0$ for all non-zero vectors $v \in {\bf N} ^ { n }$. The converse implication does not hold in general, but it has been established if the Auslander–Reiten quiver of $R$ (see Riedtmann classification) has a post-projective component (see [a10]), by applying an idea of Drozd [a5]. J.A. de la Peña [a14] proved that if $R$ is of tame representation type, then $q_{ R}$ is weakly non-negative. The converse implication does not hold in general, but it has been proved under a suitable assumption on $R$ (see [a13] and [a16] for a discussion of this problem and relations between the Tits quadratic form and the Euler quadratic form of $R$).
Let $( I , \preceq )$ be a partially ordered set with partial order relation $\preceq$ and let $\operatorname { max}I$ be the set of all maximal elements of $( I , \preceq )$. Following [a5] and [a15], D. Simson [a20] defined the Tits quadratic form $q_l : \mathbf{Z} ^ { l } \rightarrow \mathbf{Z}$ of $( I , \preceq )$ by the formula
\begin{equation*} q _I( x ) = \sum _ { i \in I } x _ { i } ^ { 2 } + \sum _ { \substack {i \prec j} \\{j\in I\backslash \operatorname {max} I} } x _ { i } x _ { j } - \sum _ { p \in \operatorname { max } I } ( \sum _ { i \prec p } x _ { i } ) x _ { p } \end{equation*}
and applied it in the study of prinjective $KI$-modules, that is, finite-dimensional right modules $X$ over the incidence $K$-algebra $K I = K ( I , \preceq )$ of $( I , \preceq )$ such that there is an exact sequence $0 \rightarrow P _ { 1 } \rightarrow P _ { 0 } \rightarrow X \rightarrow 0$, where $P_0$ is a projective $KI$-module and $P _ { 1 }$ is a direct sum of simple projectives. The additive Krull–Schmidt category $\operatorname { prin } K I$ of prinjective $KI$-modules is equivalent to the category of matrix $K$-representations of $( I , \preceq )$ [a20]. Under an identification $K_{0} ( \operatorname { prin } K I ) \simeq \mathbf{Z} ^ { I }$, the Tits form $q_{l}$ is equal to the Euler characteristic $\chi _ { K I } : K _ { 0 } ( \operatorname { prin } K I ) \rightarrow \bf Z$. A Tits-type equality is also valid for $q_{l}$ [a15]. It has been proved in [a20] that $q_{l}$ is weakly positive if and only if $\operatorname { prin } K I$ has only a finite number of iso-classes of indecomposable modules. By [a15], if $\operatorname { prin } K I$ is of tame representation type, then $q_{l}$ is weakly non-negative. The converse implication does not hold in general, but it has been proved under some assumption on $( I , \preceq )$ (see [a11]).
A Tits quadratic form $q _ { \Lambda } : \mathbf{Z} ^ { n } \rightarrow \mathbf{Z}$ for a class of classical $D$-orders $\Lambda$, where $D$ is a complete discrete valuation domain, has been defined in [a21]. Criteria for the finite lattice type and tame lattice type of $\Lambda$ are given in [a21] by means of $q _ { \Lambda }$.
For a class of $K$-co-algebras $C$, a Tits quadratic form $q _ { C } : \mathbf{Z} ^ { ( l _ { C } ) } \rightarrow \mathbf{Z}$ is defined in [a22], and the co-module types of $C$ are studied by means of $q_{C}$, where $I _ { C }$ is a complete set of pairwise non-isomorphic simple left $C$-co-modules and ${\bf Z} ^ { ( I _ { C } ) }$ is a free Abelian group of rank $| I _ { C } |$.
References
| [a1] | V.I. Auslander, I. Reiten, S. Smalø, "Representation theory of Artin algebras" , Studies Adv. Math. , 36 , Cambridge Univ. Press (1995) MR1314422 Zbl 0834.16001 |
| [a2] | I.N. Bernstein, I.M. Gelfand, V.A. Ponomarev, "Coxeter functors and Gabriel's theorem" Russian Math. Surveys , 28 (1973) pp. 17–32 Uspekhi Mat. Nauk. , 28 (1973) pp. 19–33 MR393065 |
| [a3] | K. Bongartz, "Algebras and quadratic forms" J. London Math. Soc. , 28 (1983) pp. 461–469 MR0724715 Zbl 0532.16020 |
| [a4] | V. Dlab, C.M. Ringel, "Indecomposable representations of graphs and algebras" , Memoirs , 173 , Amer. Math. Soc. (1976) MR0447344 Zbl 0332.16015 |
| [a5] | Yu.A. Drozd, "Coxeter transformations and representations of partially ordered sets" Funkts. Anal. Prilozhen. , 8 (1974) pp. 34–42 (In Russian) MR0351924 Zbl 0356.06003 |
| [a6] | Yu.A. Drozd, "On tame and wild matrix problems" , Matrix Problems , Akad. Nauk. Ukr. SSR., Inst. Mat. Kiev (1977) pp. 104–114 (In Russian) MR498704 |
| [a7] | Yu.A. Drozd, "Tame and wild matrix problems" , Representations and Quadratic Forms (1979) pp. 39–74 (In Russian) MR0600111 Zbl 0454.16014 |
| [a8] | P. Gabriel, "Unzerlegbare Darstellungen 1" Manuscripta Math. , 6 (1972) pp. 71–103 (Also: Berichtigungen 6 (1972), 309) MR332887 |
| [a9] | P. Gabriel, "Représentations indécomposables" , Séminaire Bourbaki (1973/74) , Lecture Notes in Mathematics , 431 , Springer (1975) pp. 143–169 MR0485996 Zbl 0335.17005 |
| [a10] | P. Gabriel, A.V. Roiter, "Representations of finite dimensional algebras" , Algebra VIII , Encycl. Math. Stud. , 73 , Springer (1992) MR1239446 MR1239447 Zbl 0839.16001 |
| [a11] | S. Kasjan, D. Simson, "Tame prinjective type and Tits form of two-peak posets II" J. Algebra , 187 (1997) pp. 71–96 MR1425560 Zbl 0944.16013 |
| [a12] | L.A. Nazarova, "Representations of quivers of infinite type" Izv. Akad. Nauk. SSSR , 37 (1973) pp. 752–791 (In Russian) MR0338018 Zbl 0298.15012 |
| [a13] | J.A. de la Peña, "Algebras with hypercritical Tits form" , Topics in Algebra , Banach Center Publ. , 26: 1 , PWN (1990) pp. 353–369 Zbl 0731.16008 |
| [a14] | J.A. de la Peña, "On the dimension of the module-varieties of tame and wild algebras" Commun. Algebra , 19 (1991) pp. 1795–1807 Zbl 0818.16013 |
| [a15] | J.A. de la Peña, D. Simson, "Prinjective modules, reflection functors, quadratic forms and Auslander–Reiten sequences" Trans. Amer. Math. Soc. , 329 (1992) pp. 733–753 MR1025753 Zbl 0789.16010 |
| [a16] | J.A. de la Peña, A. Skowroński, "The Euler and Tits forms of a tame algebra" Math. Ann. , 315 (2000) pp. 37–59 Zbl 0941.16010 |
| [a17] | C.M. Ringel, "Tame algebras and integral quadratic forms" , Lecture Notes in Mathematics , 1099 , Springer (1984) MR0774589 Zbl 0546.16013 |
| [a18] | A.V. Roiter, M.M. Kleiner, "Representations of differential graded categories" , Lecture Notes in Mathematics , 488 , Springer (1975) pp. 316–339 MR0435145 Zbl 0356.16011 |
| [a19] | D. Simson, "Linear representations of partially ordered sets and vector space categories" , Algebra, Logic Appl. , 4 , Gordon & Breach (1992) MR1241646 Zbl 0818.16009 |
| [a20] | D. Simson, "Posets of finite prinjective type and a class of orders" J. Pure Appl. Algebra , 90 (1993) pp. 77–103 MR1246276 Zbl 0815.16006 |
| [a21] | D. Simson, "Representation types, Tits reduced quadratic forms and orbit problems for lattices over orders" Contemp. Math. , 229 (1998) pp. 307–342 MR1676228 Zbl 0921.16007 |
| [a22] | D. Simson, "Coalgebras, comodules, pseudocompact algebras and tame comodule type" Colloq. Math. , in press (2001) MR1874368 Zbl 1055.16038 |
Tits quadratic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tits_quadratic_form&oldid=54339