Specht module

Let $n \in \mathbf N$ and suppose $\lambda$ is a (proper) partition of $n$. This means that $\lambda = ( \lambda _ { 1 } \geq \lambda _ { 2 } \geq \ldots \geq 0 )$, where each $\lambda _ { i } \in \bf Z$ and $\sum _ { i } \lambda _ { i } = n$. If $r$ is maximal with $\lambda _ { r } > 0$, then one says that $\lambda$ is a partition of $n$ into $r$ parts.

A $\lambda$-tableau (sometimes called a Young tableau associated with $\lambda$) is an array consisting of the numbers $1 , \dots , n$ listed in $r$ rows with exactly $\lambda _ { i }$ numbers occurring in the $i$th row, $ i = 1 , \ldots , r$. If, for instance, $n = 9$ and $\lambda = ( 4,3,1,1 )$, then the following arrays are examples of $\lambda$-tableaux:

\begin{equation*} \left. \begin{array} { l l l l l l l l l } { 1 } & { 2 } & { 3 } & { 4 } & { } & { 9 } & { 2 } & { 3 } & { 6 } \\ { 5 } & { 6 } & { 7 } & { } & { \text { and } } & { 7 } & { 1 } & { 4 } & { } \\ { 8 } & { } & { } & { } & { } & { 5 } & { } & { } & { } \\ { 9 } & { } & { } & { } & { } & { 8 } & { } & { } & { } \end{array} \right. \end{equation*}

One says that two $\lambda$-tableaux are equivalent if for each $ i = 1 , \ldots , r$ the two sets of numbers in the $i$th rows of the two arrays coincide. Clearly, the two $\lambda$-tableaux above are not equivalent. The equivalence classes with respect to this relation are called $\lambda$-tabloids. If $t$ is a $\lambda$-tableau, one usually denotes the $\lambda$-tabloid by $\{ t \}$. As examples, for $\lambda$ as above one has

\begin{equation*} \left( \begin{array} { c c c c } { 1 } & { 2 } & { 3 } & { 4 } \\ { 5 } & { 6 } & { 7 } & { } \\ { 8 } & { } & { } & { } \\ { 9 } & { } & { } & { } \end{array} \right) = \left( \begin{array} { c c c c } { 4 } & { 2 } & { 1 } & { 3 } \\ { 6 } & { 5 } & { 7 } & { } \\ { 8 } & { } & { } & { } \\ { 9 } & { } & { } & { } \end{array} \right) \neq \end{equation*}

\begin{equation*} \neq \left( \begin{array} { c c c c } { 9 } & { 2 } & { 3 } & { 6 } \\ { 7 } & { 1 } & { 4 } & { } \\ { 8 } & { } & { } & { } \\ { 9 } & { } & { } & { } \end{array} \right) = \left( \begin{array} { c c c c } { 2 } & { 3 } & { 9 } & { 6 } \\ { 4 } & { 1 } & { 7 } & { } \\ { 8 } & { } & { } & { } \\ { 9 } & { } & { } & { } \end{array} \right). \end{equation*}

Suppose $k$ is a field. Denote by $M ^ { \lambda }$ the vector space over $k$ with basis equal to the set of $\lambda$-tabloids. Then the symmetric group $S _ { n }$ on $n$ letters (cf. also Symmetric group) acts on $M ^ { \lambda }$ (or, more precisely, $M ^ { \lambda }$ is a $k S _ { n }$-module) in a natural way. Indeed, if $\sigma \in S _ { n }$ and $t$ is a $\lambda$-tableau, then $\sigma t $ is the $\lambda$-tableau obtained from $t$ by replacing each number $i$ by $\sigma i$. If one uses the usual cycle presentation of elements in $S _ { n }$, then, e.g., for $\sigma = ( 452 ) ( 89 ) ( 316 ) \in S_{9}$ one has

\begin{equation*} \sigma \left( \begin{array} { c c c c } { 9 } & { 2 } & { 3 } & { 6 } \\ { 7 } & { 1 } & { 4 } & { } \\ { 5 } & { } & { } & { } \\ { 8 } & { } & { } & { } \end{array} \right) = \left( \begin{array} { c c c c } { 8 } & { 4 } & { 1 } & { 3 } \\ { 7 } & { 6 } & { 5 } & { } \\ { 2 } & { } & { } & { } \\ { 9 } & { } & { } & { } \end{array} \right). \end{equation*}

This action clearly induces an action of $S _ { n }$ on $\lambda$-tabloids and this gives the desired module structure on $M ^ { \lambda }$.

If, again, $t$ is a $\lambda$-tableau, then one sets

\begin{equation*} e _ { t } = \sum _ { \pi } \operatorname { sgn } ( \pi ) \{ \pi t \}, \end{equation*}

where the sum runs over the $\pi \in S _ { n }$ that leave the set of numbers in each column in $t$ stable. Here, $\operatorname { sgn } ( \pi )$ is the sign of $\pi$.

The Specht module associated to $\lambda$ is defined as the submodule

\begin{equation*} S^{\lambda} = \operatorname{span} \{ e_t : t \text{ a }\lambda\text{-tableau } \} \end{equation*}

of $M^{\lambda}$. Clearly, $S^{\lambda}$ is invariant under the action of $S_{n}$. (In fact, $\sigma e_{t} = e_{ \sigma t}$ for all $\sigma \in S_{n}$ and all $\lambda$-tableau $t$.)

Specht modules were introduced in 1935 by W. Specht [a5]. Their importance in the representation theory for symmetric groups (cf. also Representation of the symmetric groups) comes from the fact that when $k$ contains $\mathbf{Q}$, then each $S^{\lambda}$ is a simple $k S_{n}$-module. Moreover, the set

\begin{equation*} \left\{S^{\lambda} : \lambda \text { a partition of } n \right\} \end{equation*}

is a full set of simple $k S_{n}$-modules.

When the characteristic of $k$ is $p > 0$, then the Specht modules are no longer always simple. However, they still play an important role in the classification of simple $k S_{n}$-modules. Namely, it turns out that when $\lambda$ is $p$-regular (i.e. no $p$ parts of $\lambda$ are equal), then $S^{\lambda}$ has a unique simple quotient $D^{\lambda}$ and the set

\begin{equation*} \{ D^{\lambda} : \lambda \text{ a p-regular partition of } n \} \end{equation*}

constitutes a full set of simple $k S_{n}$-modules. It is a major open problem (1999) to determine the dimensions of these modules.

It is possible to give a (characteristic-free) natural basis for $S^{\lambda}$. This is sometimes referred to as the Specht basis. In the notation above, it is given by

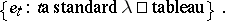Here, a $\lambda$-tableau $t$ is called standard if the numbers occurring in $t$ are increasing along each row and down each column.

An immediate consequence is that the dimension of $S^{\lambda}$ equals the number of standard $\lambda$-tableaux. For various formulas for this number (as well as many further properties of Specht modules) see [a2] and [a3].

The representation theory for symmetric groups is intimately related to the corresponding theory for general linear groups (Schur duality). Under this correspondence, Specht modules play the same role for $S_{n}$ as do the Weyl modules for $\operatorname{GL}_{n}$, see e.g. [a1] and Weyl module. For a recent result exploring this correspondence in characteristic $p > 0$, see [a4].

References

[a1]	J.A. Green, "Polynomial representations of $GL_n$" , Lecture Notes Math. , 830 , Springer (1980)
[a2]	G.D. James, "The representation theory of the symmetric groups" , Lecture Notes Math. , 682 , Springer (1978)
[a3]	G.D. James, A. Kerber, "The representation theory of the symmetric group" , Encycl. Math. Appl. , 16 , Addison-Wesley (1981)
[a4]	O. Mathieu, "On the dimension of some modular irreducible representations of the symmetric group" Lett. Math. Phys. , 38 (1996) pp. 23–32
[a5]	W. Specht, "Die irreduziblen Darstellungen der symmetrischen Gruppe" Math. Z. , 39 (1935) pp. 696–711