Contact problems of the theory of heat conduction

Problems on the propagation of heat (stationary and non-stationary, for elliptic and parabolic equations, respectively) in the case when the material is thermally inhomogeneous, that is, consists of several parts with different coefficients of thermal conductivity , heat capacity and density . The coefficients entering in the differential equation have discontinuities of the first kind. This leads to problems with weak discontinuities of the solutions, that is, the temperature is continuous and the derivatives are discontinuous. However, the heat flow is defined to be continuous.

Suppose, for example, that one has a one-dimensional heat equation in , ,

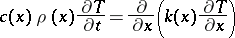(1)

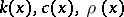and suppose that at a point the functions have discontinuities of the first kind,

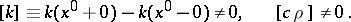Then the temperature 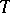and flow must be continuous at 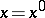(see [1], [2]),

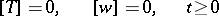(2)

(adjointness conditions). At other points of the interval the temperature 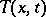must satisfy equation (1) for 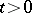, initial conditions for 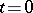, and also boundary conditions for , , .

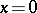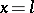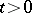In the multi-dimensional case with the parabolic equation

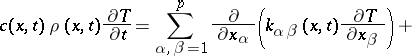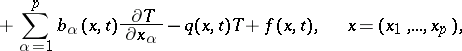one again imposes on the surface 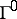of discontinuity of the coefficients the conditions (2) of continuity of the function and of the flow

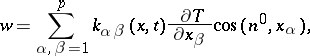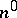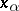where is the normal to and is the angle between and the direction of (see [3], [4]).

In the stationary case 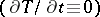, conditions (2) are imposed at the discontinuity. Sometimes more general conservation laws are imposed (see [2], [4]). E.g., in the one-dimensional case one considers the following conditions:

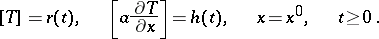Related to the contact problems of the theory of heat conduction is the problem of the propagation of heat in media whose aggregate state can change at a certain value of the temperature 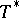(the temperature of phase transition) with emission or absorption of latent heat 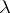(the Stefan problem, [5]). At the unknown boundary of the phase interface the following conditions are imposed in the one-dimensional case:

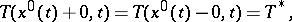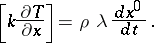There are a large number of contact problems for systems of equations of heat conduction and for equations related to gas dynamics and magneto-hydrodynamics.

References

[1]	A.A. Samarskii, "Parabolic equations with discontinuous coefficients" Dokl. Akad. Nauk SSSR , 121 : 2 (1958) pp. 225–228 (In Russian)
[2]	L.I. Kamynin, Sibirsk. Mat. Zh. , 4 : 5 (1963) pp. 1071–1105
[3]	O.A. Oleinik, "Boundary value problems for linear equations of elliptic-parabolic type with discontinuous coefficients" Izv. Akad. Nauk SSSR Ser. Mat. , 25 : 1 (1961) pp. 3–20 (In Russian)
[4]	L.I. Kamynin, "Smoothness of heat potentials V" Differential Equations , 3 : 6 (1967) pp. 496–504 Differentsial'nye Uravneniya , 3 : 6 (1967) pp. 948–964
[5]	A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)
[6]	O.A. Ladyzhenskaya, N.N. Ural'tseva, "Linear and quasilinear elliptic equations" , Acad. Press (1968) (Translated from Russian)