Difference between revisions of "Cylinder coordinates"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
|||
| Line 163: | Line 163: | ||
half-planes $ ( v = \textrm{ const } ) $ | half-planes $ ( v = \textrm{ const } ) $ | ||
and planes $ ( w = \textrm{ const } ) $. | and planes $ ( w = \textrm{ const } ) $. | ||
| − | |||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> U.G. Chambers, "A course in vector analysis" , Chapman & Hall (1969)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> U.G. Chambers, "A course in vector analysis" , Chapman & Hall (1969)</TD></TR></table> | ||
| + | |||
| + | |||
| + | {{OldImage}} | ||
Latest revision as of 11:19, 26 March 2023
cylindrical coordinates
Numbers $ \rho , \phi $ and $ z $ connected with the Cartesian coordinates $ x, y $ and $ z $ by the formulas:
$$ x = \rho \cos \phi ,\ \ y = \rho \sin \phi ,\ \ z = z, $$
where $ 0 \leq \rho < \infty $, $ 0 \leq \phi < 2 \pi $, $ - \infty < z < \infty $. The coordinate surfaces (see Fig.) are: circular cylinders $ ( \rho = \textrm{ const } ) $, half-planes $ ( \phi = \textrm{ const } ) $ and planes $ ( z = \textrm{ const } ) $.
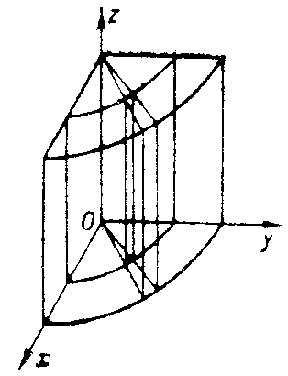
Figure: c027600a
The system of cylinder coordinates is orthogonal.
The Lamé coefficients are:
$$ L _ \rho = \ L _ {z} = 1,\ \ L _ \phi = \rho . $$
The area element of a surface is:
$$ ds = \ \sqrt {\rho ^ {2} ( d \rho d \phi ) ^ {2} + ( d \rho dz) ^ {2} + \rho ^ {2} ( d \phi dz) ^ {2} } . $$
The volume element is:
$$ dV = \rho d \rho d \phi dz. $$
The differentiation operations of vector analysis are given by:
$$ \mathop{\rm grad} _ \rho f = \ \frac{\partial f }{\partial \rho } ,\ \ \mathop{\rm grad} _ \phi f = \ { \frac{1} \rho } \frac{\partial f }{\partial \phi } ,\ \ \mathop{\rm grad} _ {z} f = \ \frac{\partial f }{\partial z } ; $$
$$ \mathop{\rm div} \mathbf a = { \frac{1} \rho } a _ \rho + \frac{\partial a _ \rho }{\partial \rho } + { \frac{1} \rho } \frac{\partial a _ \phi }{\partial \phi } + \frac{\partial a _ {z} }{\partial z } ; $$
$$ \mathop{\rm curl} _ \rho \mathbf a = { \frac{1} \rho } \frac{\partial a _ {z} }{\partial \phi } - \frac{\partial a _ \phi }{\partial z } ,\ \mathop{\rm curl} _ \phi \mathbf a = \ \frac{\partial a _ \rho }{\partial z } - \frac{\partial a _ {z} }{\partial \rho } ; $$
$$ \mathop{\rm curl} _ {z} \mathbf a = { \frac{1} \rho } a _ \phi + \frac{\partial a _ \phi }{\partial \rho } - { \frac{1} \rho } \frac{\partial a _ \rho }{\partial \phi } ; $$
$$ \Delta f = \frac{\partial ^ {2} f }{\partial \rho ^ {2} } + { \frac{1} \rho } \frac{\partial f }{\partial \rho } + { \frac{1}{ \rho ^ {2} } } \frac{\partial ^ {2} f }{\partial \phi ^ {2} } + \frac{\partial ^ {2} \phi }{\partial z ^ {2} } . $$
Generalized cylinder coordinates are numbers $ u , v $ and $ w $ connected with Cartesian coordinates $ x, y $ and $ z $ by the formulas
$$ x = au \cos v ,\ \ y = bu \sin v ,\ \ z = cw, $$
where $ 0 \leq u < \infty $, $ 0 \leq v < 2 \pi $, $ - \infty < w < \infty $, $ a > 0 $, $ b > 0 $, $ c > 0 $, $ a \neq b $. The coordinate surfaces are: elliptic cylinders $ ( u = \textrm{ const } ) $, half-planes $ ( v = \textrm{ const } ) $ and planes $ ( w = \textrm{ const } ) $.
References
| [a1] | U.G. Chambers, "A course in vector analysis" , Chapman & Hall (1969) |
Cylinder coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cylinder_coordinates&oldid=53408