Difference between revisions of "Auto-regression"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|want}} | ||
| + | |||
A regressive dependence of the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139701.png" /> of a given random sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139702.png" /> on the preceding values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139703.png" />. A linear auto-regression scheme of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139704.png" /> is defined by a linear [[Regression|regression]] equation between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139705.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139706.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139707.png" />, i.e. | A regressive dependence of the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139701.png" /> of a given random sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139702.png" /> on the preceding values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139703.png" />. A linear auto-regression scheme of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139704.png" /> is defined by a linear [[Regression|regression]] equation between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139705.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139706.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139707.png" />, i.e. | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139708.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139708.png" /></td> <td valign="top" style="width:5%;text-align:right;">(*)</td></tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139709.png" /> are constants and the random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a01397010.png" /> are identically distributed with average zero, variance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a01397011.png" /> and are uncorrelated (sometimes they are assumed to be independent). An auto-regression scheme is a useful stochastic model for the description of certain [[Time series|time series]] (the concept of a linear auto-regression scheme was first introduced by G. Yule in 1921) in order to analyze time series describing a system which is oscillating under the effect of internal forces and random external shocks. The auto-regression scheme (*) may be regarded as a stochastic process of a special type: an [[Auto-regressive process|auto-regressive process]]. | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a0139709.png" /> are constants and the random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a01397010.png" /> are identically distributed with average zero, variance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013970/a01397011.png" /> and are uncorrelated (sometimes they are assumed to be independent). An auto-regression scheme is a useful stochastic model for the description of certain [[Time series|time series]] (the concept of a linear auto-regression scheme was first introduced by [[Yule, George Udny|G. Yule]] in 1921) in order to analyze time series describing a system which is oscillating under the effect of internal forces and random external shocks. The auto-regression scheme (*) may be regarded as a stochastic process of a special type: an [[Auto-regressive process|auto-regressive process]]. |
Revision as of 14:49, 18 March 2023
A regressive dependence of the values of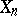 
of a given random sequence 
on the preceding values of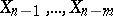 
. A linear auto-regression scheme of order 
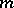is defined by a linear regression equation between 
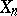and 
, 
, i.e.
 | (*) |
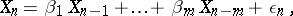where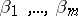 
are constants and the random variables 
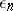are identically distributed with average zero, variance 
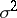and are uncorrelated (sometimes they are assumed to be independent). An auto-regression scheme is a useful stochastic model for the description of certain time series (the concept of a linear auto-regression scheme was first introduced by G. Yule in 1921) in order to analyze time series describing a system which is oscillating under the effect of internal forces and random external shocks. The auto-regression scheme (*) may be regarded as a stochastic process of a special type: an auto-regressive process.
How to Cite This Entry:
Auto-regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Auto-regression&oldid=52903
Auto-regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Auto-regression&oldid=52903
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article