Difference between revisions of "Dehn surgery"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
m (fixing spaces) |
||
| Line 12: | Line 12: | ||
Let $ M $ | Let $ M $ | ||
| − | be a closed $ 3 $- | + | be a closed $ 3 $-dimensional [[Manifold|manifold]] and let $ N $ |
| − | dimensional [[Manifold|manifold]] and let $ N $ | ||
be a solid torus in the interior of $ M $. | be a solid torus in the interior of $ M $. | ||
Remove $ { \mathop{\rm Int} } N $ | Remove $ { \mathop{\rm Int} } N $ | ||
| Line 19: | Line 18: | ||
and glue in instead of it another solid torus $ N _ {1} $ | and glue in instead of it another solid torus $ N _ {1} $ | ||
by a [[Homeomorphism|homeomorphism]] $ h : {\partial N _ {1} } \rightarrow {\partial N } $. | by a [[Homeomorphism|homeomorphism]] $ h : {\partial N _ {1} } \rightarrow {\partial N } $. | ||
| − | One says that the resulting new $ 3 $- | + | One says that the resulting new $ 3 $-dimensional manifold |
| − | dimensional manifold | ||
$$ | $$ | ||
| Line 27: | Line 25: | ||
is obtained from $ M $ | is obtained from $ M $ | ||
by a Dehn surgery. Note that $ M _ {1} $ | by a Dehn surgery. Note that $ M _ {1} $ | ||
| − | is determined by the following data: 1) a knot $ K \subset M $( | + | is determined by the following data: 1) a knot $ K \subset M $ (a core circle $ \{ * \} \times S ^ {1} $ |
| − | a core circle $ \{ * \} \times S ^ {1} $ | ||
of the solid torus $ N = D ^ {2} \times S ^ {1} $, | of the solid torus $ N = D ^ {2} \times S ^ {1} $, | ||
| − | cf. also [[Knot theory|Knot theory]]); and 2) a non-trivial simple closed curve $ l \subset \partial N $( | + | cf. also [[Knot theory|Knot theory]]); and 2) a non-trivial simple closed curve $ l \subset \partial N $ (the image under $ h $ |
| − | the image under $ h $ | ||
of a meridian of $ N _ {1} $). | of a meridian of $ N _ {1} $). | ||
The Dehn surgery is called integer if $ l $ | The Dehn surgery is called integer if $ l $ | ||
| Line 56: | Line 52: | ||
be two handle-bodies having the same genus (cf. [[Handle theory|Handle theory]]) and let $ h : {\partial H } \rightarrow {\partial H ^ \prime } $ | be two handle-bodies having the same genus (cf. [[Handle theory|Handle theory]]) and let $ h : {\partial H } \rightarrow {\partial H ^ \prime } $ | ||
be a [[Homeomorphism|homeomorphism]]. Denote by $ M $ | be a [[Homeomorphism|homeomorphism]]. Denote by $ M $ | ||
| − | the closed $ 3 $- | + | the closed $ 3 $-dimensional manifold $ H \cap _ {h} H ^ \prime $ |
| − | dimensional manifold $ H \cap _ {h} H ^ \prime $ | ||
obtained by gluing $ H $ | obtained by gluing $ H $ | ||
and $ H ^ \prime $ | and $ H ^ \prime $ | ||
| Line 93: | Line 88: | ||
the framing $ \varphi ( K ) $ | the framing $ \varphi ( K ) $ | ||
as the parameter $ r $ | as the parameter $ r $ | ||
| − | of the surgery, one obtains a $ 3 $- | + | of the surgery, one obtains a $ 3 $-dimensional manifold $ \chi ( {\mathsf L} ) $. |
| − | dimensional manifold $ \chi ( {\mathsf L} ) $. | + | Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [[#References|[a1]]], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable $ 3 $-dimensional manifold $ M $ |
| − | Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [[#References|[a1]]], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable $ 3 $- | ||
| − | dimensional manifold $ M $ | ||
there exists a framed link $ {\mathsf L} \subset S ^ {3} $ | there exists a framed link $ {\mathsf L} \subset S ^ {3} $ | ||
such that $ M = \chi ( {\mathsf L} ) $. | such that $ M = \chi ( {\mathsf L} ) $. | ||
| − | The following question naturally arises: When do two framed links determine homeomorphic $ 3 $- | + | The following question naturally arises: When do two framed links determine homeomorphic $ 3 $-dimensional manifolds? In 1978 R. Kirby answered this question by showing that $ \chi ( { {\mathsf L} _ {1} } ) = \chi ( { {\mathsf L} _ {2} } ) $ |
| − | dimensional manifolds? In 1978 R. Kirby answered this question by showing that $ \chi ( { {\mathsf L} _ {1} } ) = \chi ( { {\mathsf L} _ {2} } ) $ | ||
if and only if one can pass from $ { {\mathsf L} _ {1} } $ | if and only if one can pass from $ { {\mathsf L} _ {1} } $ | ||
to $ { {\mathsf L} _ {2} } $ | to $ { {\mathsf L} _ {2} } $ | ||
| Line 111: | Line 103: | ||
is a new unknotted component with framing $ \pm 1 $ | is a new unknotted component with framing $ \pm 1 $ | ||
such that $ {\mathsf O} $ | such that $ {\mathsf O} $ | ||
| − | is contained in a $ 3 $- | + | is contained in a $ 3 $-dimensional ball $ B ^ {3} \subset S ^ {3} $, |
| − | dimensional ball $ B ^ {3} \subset S ^ {3} $, | ||
$ B ^ {3} \cap {\mathsf L} = \emptyset $; | $ B ^ {3} \cap {\mathsf L} = \emptyset $; | ||
| Line 119: | Line 110: | ||
$ i \neq j $, | $ i \neq j $, | ||
of $ l _ {i} $ | of $ l _ {i} $ | ||
| − | with another component $ l _ {j} \subset {\mathsf L} $( | + | with another component $ l _ {j} \subset {\mathsf L} $ (see [[#References|[a2]]] for the exact definition of the geometric sum). |
| − | see [[#References|[a2]]] for the exact definition of the geometric sum). | ||
| − | This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting $ 3 $- | + | This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting $ 3 $-dimensional manifolds. |
| − | dimensional manifolds. | ||
Recall that a framing of a knot $ K \subset S ^ {3} $ | Recall that a framing of a knot $ K \subset S ^ {3} $ | ||
| Line 131: | Line 120: | ||
of $ K $. | of $ K $. | ||
Denote by $ W ^ {4} ( {\mathsf K} ) $ | Denote by $ W ^ {4} ( {\mathsf K} ) $ | ||
| − | the $ 4 $- | + | the $ 4 $-dimensional manifold $ B ^ {4} \cup _ {h} H ^ {4} $ |
| − | dimensional manifold $ B ^ {4} \cup _ {h} H ^ {4} $ | + | obtained by attaching a $ 4 $-dimensional handle $ H $ |
| − | obtained by attaching a $ 4 $- | ||
| − | dimensional handle $ H $ | ||
of index $ 2 $ | of index $ 2 $ | ||
| − | to the $ 4 $- | + | to the $ 4 $-dimensional ball via the homeomorphism $ h $ |
| − | dimensional ball via the homeomorphism $ h $ | ||
between $ D ^ {2} \times S ^ {1} \subset D ^ {2} \times D ^ {2} = H ^ {4} $ | between $ D ^ {2} \times S ^ {1} \subset D ^ {2} \times D ^ {2} = H ^ {4} $ | ||
and $ N \subset S ^ {3} = \partial D ^ {4} $. | and $ N \subset S ^ {3} = \partial D ^ {4} $. | ||
It follows from the definition that $ \partial W ^ {4} ( {\mathsf K} ) = \chi ( {\mathsf K} ) $. | It follows from the definition that $ \partial W ^ {4} ( {\mathsf K} ) = \chi ( {\mathsf K} ) $. | ||
Similarly, for any framed link $ {\mathsf L} $ | Similarly, for any framed link $ {\mathsf L} $ | ||
| − | the $ 3 $- | + | the $ 3 $-dimensional manifold $ \chi ( {\mathsf L} ) $ |
| − | dimensional manifold $ \chi ( {\mathsf L} ) $ | + | is the boundary of the $ 4 $-dimensional manifold $ W ^ {4} ( {\mathsf L} ) $ |
| − | is the boundary of the $ 4 $- | ||
| − | dimensional manifold $ W ^ {4} ( {\mathsf L} ) $ | ||
obtained by attaching handles of index $ 2 $ | obtained by attaching handles of index $ 2 $ | ||
| − | to the $ 4 $- | + | to the $ 4 $-dimensional ball. Move 1) on $ {\mathsf L} $ |
| − | dimensional ball. Move 1) on $ {\mathsf L} $ | ||
corresponds to replacing $ W ( {\mathsf L} ) $ | corresponds to replacing $ W ( {\mathsf L} ) $ | ||
by a connected sum of $ W ( {\mathsf L} ) $ | by a connected sum of $ W ( {\mathsf L} ) $ | ||
| Line 155: | Line 138: | ||
over another and does not change $ W ( {\mathsf L} ) $. | over another and does not change $ W ( {\mathsf L} ) $. | ||
One can show that any framed link in $ S ^ {3} $ | One can show that any framed link in $ S ^ {3} $ | ||
| − | can be transformed by moves 1), 2) and their inverses to a link with even framings [[#References|[a3]]]. In the latter case the tangent bundle of the corresponding $ 4 $- | + | can be transformed by moves 1), 2) and their inverses to a link with even framings [[#References|[a3]]]. In the latter case the tangent bundle of the corresponding $ 4 $-dimensional manifold is trivial. |
| − | dimensional manifold is trivial. | ||
See [[#References|[a4]]] for more details. | See [[#References|[a4]]] for more details. | ||
Revision as of 08:05, 21 March 2022
Let $ M $
be a closed $ 3 $-dimensional manifold and let $ N $
be a solid torus in the interior of $ M $.
Remove $ { \mathop{\rm Int} } N $
from $ M $
and glue in instead of it another solid torus $ N _ {1} $
by a homeomorphism $ h : {\partial N _ {1} } \rightarrow {\partial N } $.
One says that the resulting new $ 3 $-dimensional manifold
$$ M _ {1} = ( M \setminus { \mathop{\rm Int} } N ) \cup _ {h} N _ {1} $$
is obtained from $ M $ by a Dehn surgery. Note that $ M _ {1} $ is determined by the following data: 1) a knot $ K \subset M $ (a core circle $ \{ * \} \times S ^ {1} $ of the solid torus $ N = D ^ {2} \times S ^ {1} $, cf. also Knot theory); and 2) a non-trivial simple closed curve $ l \subset \partial N $ (the image under $ h $ of a meridian of $ N _ {1} $). The Dehn surgery is called integer if $ l $ is a longitude of $ N $, i.e., $ l $ intersects a meridional curve of $ N $ transversally in a single point.
If $ M = S ^ {3} $, then among all longitudes of $ N $ there is a preferred one, which bounds a surface in the complement of $ N $. The preferred longitude $ l _ {0} $ forms together with a meridian $ m $ of $ N $ a coordinate system on $ \partial N $. Therefore, $ l $ has the form $ l = m ^ {p} l _ {0} ^ {q} $, where $ p,q $ are coprime integers, and is determined by the rational number $ r = {p / q } $. The Dehn surgery is integer if and only if $ r $ is an integer. This explains the terminology.
Let $ H,H ^ \prime $ be two handle-bodies having the same genus (cf. Handle theory) and let $ h : {\partial H } \rightarrow {\partial H ^ \prime } $ be a homeomorphism. Denote by $ M $ the closed $ 3 $-dimensional manifold $ H \cap _ {h} H ^ \prime $ obtained by gluing $ H $ and $ H ^ \prime $ along $ h $. Choose a simple closed curve $ s \subset \partial H $ and denote by $ \tau _ {s} $ the Dehn twist along $ s $. To be more precise, $ \tau _ {s} $ is a homeomorphism $ \partial H \rightarrow \partial H $ obtained by cutting $ \partial H $ along $ s $, isotopically rotating one side of the cut by $ 2 \pi $, and gluing back. Let $ M _ {1} = H \cap _ {h \tau _ {s} } H ^ \prime $. Since $ h $ and $ h \tau _ {s} $ coincide outside a neighbourhood of $ s $ in $ \partial H $, $ M $ and $ M _ {1} $ do actually coincide outside regular neighbourhoods of $ s $ in $ M $ and $ M _ {1} $, respectively. It follows that $ M _ {1} $ is obtained from $ M $ by a Dehn surgery along $ s $. One can easily show that the surgery is integer.
Define a framed link $ {\mathsf L} $ to be a link $ L \subset S ^ {3} $ such that every component $ K $ of $ L $ is supplied with an integer number $ \varphi ( K ) $, called a framing. If one performs Dehn surgeries along all components of $ L $, taking for each component $ K \subset L $ the framing $ \varphi ( K ) $ as the parameter $ r $ of the surgery, one obtains a $ 3 $-dimensional manifold $ \chi ( {\mathsf L} ) $. Since any orientation-preserving homeomorphism of the boundary of a handle-body is isotopic to a product of Dehn twists [a1], it follows from the above relation between Dehn twists and integer Dehn surgeries that for every closed orientable $ 3 $-dimensional manifold $ M $ there exists a framed link $ {\mathsf L} \subset S ^ {3} $ such that $ M = \chi ( {\mathsf L} ) $.
The following question naturally arises: When do two framed links determine homeomorphic $ 3 $-dimensional manifolds? In 1978 R. Kirby answered this question by showing that $ \chi ( { {\mathsf L} _ {1} } ) = \chi ( { {\mathsf L} _ {2} } ) $ if and only if one can pass from $ { {\mathsf L} _ {1} } $ to $ { {\mathsf L} _ {2} } $ by a sequence of the following moves and their inverses [a2]:
1) replace $ {\mathsf L} $ by the link $ {\mathsf L} \cup {\mathsf O} $, where $ {\mathsf O} $ is a new unknotted component with framing $ \pm 1 $ such that $ {\mathsf O} $ is contained in a $ 3 $-dimensional ball $ B ^ {3} \subset S ^ {3} $, $ B ^ {3} \cap {\mathsf L} = \emptyset $;
2) replace a component $ l _ {i} \subset {\mathsf L} $ by a geometric sum $ l _ {i} + l _ {j} $, $ i \neq j $, of $ l _ {i} $ with another component $ l _ {j} \subset {\mathsf L} $ (see [a2] for the exact definition of the geometric sum).
This result became broadly known as the Kirby calculus for framed links, thanks to its convenience for presenting $ 3 $-dimensional manifolds.
Recall that a framing of a knot $ K \subset S ^ {3} $ determines a homeomorphism $ h $ of the standard solid torus $ D ^ {2} \times S ^ {1} $ onto a regular neighbourhood $ N $ of $ K $. Denote by $ W ^ {4} ( {\mathsf K} ) $ the $ 4 $-dimensional manifold $ B ^ {4} \cup _ {h} H ^ {4} $ obtained by attaching a $ 4 $-dimensional handle $ H $ of index $ 2 $ to the $ 4 $-dimensional ball via the homeomorphism $ h $ between $ D ^ {2} \times S ^ {1} \subset D ^ {2} \times D ^ {2} = H ^ {4} $ and $ N \subset S ^ {3} = \partial D ^ {4} $. It follows from the definition that $ \partial W ^ {4} ( {\mathsf K} ) = \chi ( {\mathsf K} ) $. Similarly, for any framed link $ {\mathsf L} $ the $ 3 $-dimensional manifold $ \chi ( {\mathsf L} ) $ is the boundary of the $ 4 $-dimensional manifold $ W ^ {4} ( {\mathsf L} ) $ obtained by attaching handles of index $ 2 $ to the $ 4 $-dimensional ball. Move 1) on $ {\mathsf L} $ corresponds to replacing $ W ( {\mathsf L} ) $ by a connected sum of $ W ( {\mathsf L} ) $ with $ \pm CP ^ {2} $. Move 2) corresponds to a sliding of one handle of index $ 2 $ over another and does not change $ W ( {\mathsf L} ) $. One can show that any framed link in $ S ^ {3} $ can be transformed by moves 1), 2) and their inverses to a link with even framings [a3]. In the latter case the tangent bundle of the corresponding $ 4 $-dimensional manifold is trivial.
See [a4] for more details.
References
| [a1] | W.B.R. Lickorish, "A representation of orientable combinatorial 3-manifolds" Ann. Math , 76 (1962) pp. 531–540 |
| [a2] | R. Kirby, "A calculus for framed links in 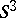 " Invent. Math. , 45 (1978) pp. 35–56 " Invent. Math. , 45 (1978) pp. 35–56 |
| [a3] | S. Kaplan, "Constructing framed 4-manifolds with given almost framed boundaries" Trans. Amer. Math. Soc. , 254 (1979) pp. 237–263 |
| [a4] | A.T. Fomenko, S.V. Matveev, "Algorithmic and computer methods in three dimensional topology" , Kluwer Acad. Publ. (1997) |
Dehn surgery. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dehn_surgery&oldid=52241